Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T15:54:46.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluctuation dynamos at finite correlation times using renewing flows

Part of: Macroscopic Randomness

Published online by Cambridge University Press:  13 July 2015

Pallavi Bhat  and
Kandaswamy Subramanian
Pallavi Bhat*
Affiliation:
IUCAA, Post Bag 4, Ganeshkhind, Pune 411 007, India
Kandaswamy Subramanian
Affiliation:
IUCAA, Post Bag 4, Ganeshkhind, Pune 411 007, India
*
†Email address for correspondence: palvi@iucaa.ernet.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Fluctuation dynamos are generic to turbulent astrophysical systems. The only analytical model of the fluctuation dynamo, due to Kazantsev, assumes the velocity to be delta-correlated in time. This assumption breaks down for any realistic turbulent flow. We generalize the analytic model of fluctuation dynamos to include the effects of a finite correlation time, ${\it\tau}$ , using renewing flows. The generalized evolution equation for the longitudinal correlation function 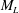$M_{L}$ leads to the standard Kazantsev equation in the 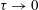${\it\tau}\rightarrow 0$ limit, and extends it to the next order in ${\it\tau}$ . We find that this evolution equation also involves third and fourth spatial derivatives of 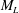$M_{L}$ , indicating that the evolution for finite- ${\it\tau}$ will be non-local in general. In the perturbative case of small- ${\it\tau}$ (or small Strouhal number), it can be recast using the Landau–Lifschitz approach, to one with at most second derivatives of 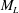$M_{L}$ . Using both a scaling solution and the WKBJ approximation, we show that the dynamo growth rate is reduced when the correlation time is finite. Interestingly, to leading order in ${\it\tau}$ , we show that the magnetic power spectrum preserves the Kazantsev form, 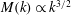$M(k)\propto k^{3/2}$ , in the large- 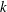$k$ limit, independent of ${\it\tau}$ .

Type
Research Article
Information
Journal of Plasma Physics , Volume 81 , Issue 5 , October 2015 , 395810502
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
Beresnyak, A. 2012 Universal nonlinear small-scale dynamo. Phys. Rev. Lett. 108 (3), 035002.Google Scholar
Bhat, P. & Subramanian, K. 2013 Fluctuation dynamos and their Faraday rotation signatures. Mon. Not. R. Astron. Soc. 429, 2469–2481.Google Scholar
Bhat, P. & Subramanian, K. 2014 Fluctuation dynamo at finite correlation times and the Kazantsev spectrum. Astrophys. J. 791, L34, 5pp.Google Scholar
Brandenburg, A., Sokoloff, D. & Subramanian, K. 2012 Current status of turbulent dynamo theory. From large-scale to small-scale dynamos. Space Sci. Rev. 169, 123–157.Google Scholar
Brandenburg, A. & Subramanian, K. 2000 Large scale dynamos with ambipolar diffusion nonlinearity. Astron. Astrophys. 361, L33–L36.Google Scholar
Brandenburg, A. & Subramanian, K. 2005 Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 417, 1–209.Google Scholar
Chandran, B. D. G. 1997 The effects of velocity correlation times on the turbulent amplification of magnetic energy. Astrophys. J. 482, 156–166.Google Scholar
Chertkov, M., Falkovich, G., Kolokolov, I. & Vergassola, M. 1999 Small-scale turbulent dynamo. Phys. Rev. Lett. 83, 4065–4068.Google Scholar
Cho, J., Vishniac, E. T., Beresnyak, A., Lazarian, A. & Ryu, D. 2009 Growth of magnetic fields induced by turbulent motions. Astrophys. J. 693, 1449–1461.Google Scholar
Dittrich, P., Molchanov, S. A., Sokolov, D. D. & Ruzmaikin, A. A. 1984 Mean magnetic field in renovating random flow. Astron. Nachr. 305, 119–125.Google Scholar
Enßlin, T. A. & Vogt, C. 2006 Magnetic turbulence in cool cores of galaxy clusters. Astron. Astrophys. 453, 447–458.Google Scholar
Federrath, C., Chabrier, G., Schober, J., Banerjee, R., Klessen, R. S. & Schleicher, D. R. G. 2011 Mach number dependence of turbulent magnetic field amplification: solenoidal versus compressive flows. Phys. Rev. Lett. 107 (11), 114504.Google Scholar
Gilbert, A. D. & Bayly, B. J. 1992 Magnetic field intermittency and fast dynamo action in random helical flows. J. Fluid Mech. 241, 199–214.Google Scholar
Gruzinov, A., Cowley, S. & Sudan, R. 1996 Small-scale-field dynamo. Phys. Rev. Lett. 77, 4342–4345.Google Scholar
Haugen, N. E., Brandenburg, A. & Dobler, W. 2004 Simulations of nonhelical hydromagnetic turbulence. Phys. Rev. E 70 (1), 016308.Google Scholar
Holden, H., Karlsen, K. H., Li, K.-A. & Risebro, N. H 2010 Splitting Methods for Partial Differential Equations with Rough Solutions: Analysis and MATLAB Programs. European Mathematical Society.Google Scholar
Kazantsev, A. P. 1967 Enhancement of a magnetic field by a conducting fluid. JETP 53, 1807–1813; English translation, 1968: Sov. Phys. JETP 26, 1031–1034.Google Scholar
Kleeorin, N., Rogachevskii, I. & Sokoloff, D. 2002 Magnetic fluctuations with a zero mean field in a random fluid flow with a finite correlation time and a small magnetic diffusion. Phys. Rev. E 65 (3), 036303.Google Scholar
Kolekar, S., Subramanian, K. & Sridhar, S. 2012 Mean-field dynamo action in renovating shearing flows. Phys. Rev. E 86 (2), 026303.Google Scholar
Kulsrud, R. M. & Anderson, S. W. 1992 The spectrum of random magnetic fields in the mean field dynamo theory of the Galactic magnetic field. Astrophys. J. 396, 606–630.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1975 The Classical Theory of Fields. Pergamon.Google Scholar
Malyshkin, L. M. & Boldyrev, S. 2010 Magnetic dynamo action at low magnetic Prandtl numbers. Phys. Rev. Lett. 105 (21), 215002.Google Scholar
Mason, J., Malyshkin, L., Boldyrev, S. & Cattaneo, F. 2011 Magnetic dynamo action in random flows with zero and finite correlation times. Astrophys. J. 730, 86, 7pp.Google Scholar
Mestel, L. & Subramanian, K. 1991 Galactic dynamos and density wave theory. Mon. Not. R. Astron. Soc. 248, 677–687.Google Scholar
Molchanov, S. A., Ruzmaĭkin, A. A. & Sokolov, D. D. 1985 Reviews of topical problems: kinematic dynamo in random flow. Sov. Phys. Uspekhi 28, 307–327.CrossRefGoogle Scholar
Rogachevskii, I. & Kleeorin, N. 1997 Intermittency and anomalous scaling for magnetic fluctuations. Phys. Rev. E 56, 417–426.CrossRefGoogle Scholar
Schekochihin, A. A., Boldyrev, S. A. & Kulsrud, R. M. 2002 Spectra and growth rates of fluctuating magnetic fields in the kinematic dynamo theory with large magnetic Prandtl numbers. Astrophys. J. 567, 828–852.Google Scholar
Schekochihin, A. A., Cowley, S. C., Taylor, S. F., Maron, J. L. & McWilliams, J. C. 2004 Simulations of the small-scale turbulent dynamo. Astrophys. J. 612, 276–307.Google Scholar
Schekochihin, A. A., Haugen, N. E. L., Brandenburg, A., Cowley, S. C., Maron, J. L. & McWilliams, J. C. 2005 The onset of a small-scale turbulent dynamo at low magnetic Prandtl numbers. Astrophys. J. Lett. 625, L115–L118.Google Scholar
Schekochihin, A. A. & Kulsrud, R. M. 2001 Finite-correlation-time effects in the kinematic dynamo problem. Phys. Plasmas 8, 4937–4953.Google Scholar
Schober, J., Schleicher, D., Bovino, S. & Klessen, R. S. 2012 Small-scale dynamo at low magnetic Prandtl numbers. Phys. Rev. E 86 (6), 066412.Google Scholar
Subramanian, K.1997 Dynamics of fluctuating magnetic fields in turbulent dynamos incorporating ambipolar drifts. ArXiv Astrophysics e-prints. arXiv:astro-ph/9708216.Google Scholar
Subramanian, K. 1999 Unified treatment of small- and large-scale dynamos in helical turbulence. Phys. Rev. Lett. 83, 2957–2960.Google Scholar
Subramanian, K. & Brandenburg, A. 2014 Traces of large-scale dynamo action in the kinematic stage. Mon. Not. R. Astron. Soc. 445, 2930–2940.Google Scholar
Subramanian, K., Shukurov, A. & Haugen, N. E. L. 2006 Evolving turbulence and magnetic fields in galaxy clusters. Mon. Not. R. Astron. Soc. 366, 1437–1454.Google Scholar
Sur, S., Federrath, C., Schleicher, D. R. G., Banerjee, R. & Klessen, R. S. 2012 Magnetic field amplification during gravitational collapse – influence of turbulence, rotation and gravitational compression. Mon. Not. R. Astron. Soc. 423, 3148–3162.Google Scholar
Tobias, S. M., Cattaneo, F. & Boldyrev, S.2011 MHD dynamos and turbulence. ArXiv e-prints. arXiv:1103.3138.Google Scholar
Zeldovich, Ya. B., Molchanov, S. A., Ruzmaikin, A. A. & Sokoloff, D. D. 1988 Intermittency, diffusion and generation in a nonstationary random medium. Sov. Sci. Rev. C. Math. Phys. 7, 1–110.Google Scholar
Zeldovich, Ya. B., Ruzmaikin, A. A. & Sokoloff, D. D. 1990 The Almighty Chance. World Scientific.Google Scholar