Article contents
Godbillon-Vey helicity and magnetic helicity in magnetohydrodynamics
Published online by Cambridge University Press: 10 October 2019
Abstract
The Godbillon–Vey invariant occurs in homology theory, and algebraic topology, when conditions for a co-dimension 1, foliation of a three-dimensional manifold are satisfied. The magnetic Godbillon–Vey helicity invariant in magnetohydrodynamics (MHD) is a higher-order helicity invariant that occurs for flows in which the magnetic helicity density 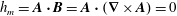 $h_{m}=\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}=\boldsymbol{A}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{A})=0$, where
$h_{m}=\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{B}=\boldsymbol{A}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{A})=0$, where 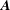 $\boldsymbol{A}$ is the magnetic vector potential and
$\boldsymbol{A}$ is the magnetic vector potential and 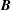 $\boldsymbol{B}$ is the magnetic induction. This paper obtains evolution equations for the magnetic Godbillon–Vey field
$\boldsymbol{B}$ is the magnetic induction. This paper obtains evolution equations for the magnetic Godbillon–Vey field 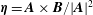 $\unicode[STIX]{x1D6C8}=\boldsymbol{A}\times \boldsymbol{B}/|\boldsymbol{A}|^{2}$ and the Godbillon–Vey helicity density
$\unicode[STIX]{x1D6C8}=\boldsymbol{A}\times \boldsymbol{B}/|\boldsymbol{A}|^{2}$ and the Godbillon–Vey helicity density 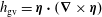 $h_{\text{gv}}=\unicode[STIX]{x1D6C8}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D6C8})$ in general MHD flows in which either
$h_{\text{gv}}=\unicode[STIX]{x1D6C8}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D6C8})$ in general MHD flows in which either 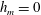 $h_{m}=0$ or
$h_{m}=0$ or 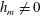 $h_{m}\neq 0$. A conservation law for
$h_{m}\neq 0$. A conservation law for 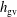 $h_{\text{gv}}$ occurs in flows for which
$h_{\text{gv}}$ occurs in flows for which 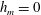 $h_{m}=0$. For
$h_{m}=0$. For 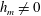 $h_{m}\neq 0$ the evolution equation for
$h_{m}\neq 0$ the evolution equation for 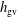 $h_{\text{gv}}$ contains a source term in which
$h_{\text{gv}}$ contains a source term in which 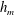 $h_{m}$ is coupled to
$h_{m}$ is coupled to 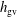 $h_{\text{gv}}$ via the shear tensor of the background flow. The transport equation for
$h_{\text{gv}}$ via the shear tensor of the background flow. The transport equation for 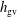 $h_{\text{gv}}$ also depends on the electric field potential
$h_{\text{gv}}$ also depends on the electric field potential 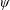 $\unicode[STIX]{x1D713}$, which is related to the gauge for
$\unicode[STIX]{x1D713}$, which is related to the gauge for 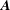 $\boldsymbol{A}$, which takes its simplest form for the advected
$\boldsymbol{A}$, which takes its simplest form for the advected 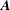 $\boldsymbol{A}$ gauge in which
$\boldsymbol{A}$ gauge in which 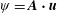 $\unicode[STIX]{x1D713}=\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{u}$ where
$\unicode[STIX]{x1D713}=\boldsymbol{A}\boldsymbol{\cdot }\boldsymbol{u}$ where  $\boldsymbol{u}$ is the fluid velocity. An application of the Godbillon–Vey magnetic helicity to nonlinear force-free magnetic fields used in solar physics is investigated. The possible uses of the Godbillon–Vey helicity in zero helicity flows in ideal fluid mechanics, and in zero helicity Lagrangian kinematics of three-dimensional advection, are discussed.
$\boldsymbol{u}$ is the fluid velocity. An application of the Godbillon–Vey magnetic helicity to nonlinear force-free magnetic fields used in solar physics is investigated. The possible uses of the Godbillon–Vey helicity in zero helicity flows in ideal fluid mechanics, and in zero helicity Lagrangian kinematics of three-dimensional advection, are discussed.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2019
References
- 6
- Cited by


