We discuss the propagation of wave packets of the form

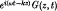
in an infinite uniform plasma, where G(z, t) is a slowly varying function of space z and time t. One can very simply derive the equation of change of G(z, t) for the stable or unstable case. The terms in the equation are of physical interest and clearly define the limitations of linear theory. We then investigate the problem of whistler mode wave propagation in a collisionless Vlasov plasma in a given non-uniform magnetic field. We choose the electric field to be of a W.K.B. form and the particle distribution to be isotropic. We can express the perturbation in the particle distribution in terms of an integration along the zero-order par tide orbits (an integration overtime). These orbits can be found correct to a term linear in a smallness parameter ε (when ε equals zero we arrive back at a uniform magnetic field). The charge and current density due to the perturbation are related through Maxwell's equations to the electric and magnetic field of the wave in the usual self consistent Boltzmann—Vlasov description. We show that the contribution to the current arises from recent events in the history of a given particle because of the finite temperature of the plasma. This result leads to an expansion of slowly varying parameters which in turn gives rise to the equation governing the motion of the wave packet.