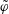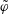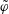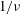1 Introduction
The transport of impurities in three-dimensional toroidal magnetic fields has attracted much attention from the stellarator community. In stellarators, the accumulation of impurities in the centre of the confinement region often limits the discharge duration and is considered to be a potential problem for the development of future reactors. In the framework of neoclassical theory, this accumulation has generally been explained with the inward convection caused by the typically negative radial electric field acting on the highly charged ions in the absence of a so-called ‘temperature screening’ effect in non-axisymmetric systems.Footnote 1 In a qualitative sense, these expectations are consistent with the general trend observed in the impurity confinement time (Burhenn et al. Reference Burhenn, Feng, Ida, Maassberg, McCarthy, Kalinina, Kobayashi, Morita, Nakamura and Nozato2009), although there are remarkable experimental observations of outward impurity transport (see, for example, McCormick et al. Reference McCormick, Grigull, Burhenn, Brakel, Ehmler, Feng, Gadelmeier, Giannone, Hildebrandt and Hirsch2002, Ida et al. Reference Ida, Yoshinuma, Osakabe, Nagaoka, Yokoyama, Funaba, Suzuki, Ido, Shimizu and Murakami2009). This outward impurity flux is still poorly understood. On a quantitative level, it is difficult to determine whether the observed impurity fluxes agree with calculations relying on the solution of approximate versions of the drift-kinetic equation, for these comparisons are often fragmented, dealing with a reduced number of plasma profiles and based on different measuring techniques. The fundamental output of neoclassical modelling of impurity transport is the spatially resolved radial particle flux of a charge state of a certain impurity species, and it is often the case that this very quantity is not experimentally accessible, which complicates the direct quantitative comparisons.
The kinetic modelling of impurity dynamics and transport has undergone recent improvements with the inclusion of terms that had previously been considered of secondary importance (García-Regaña et al.
Reference García-Regaña, Kleiber, Beidler, Turkin, Maassberg and Helander2013). These terms model the modification of the trajectories of impurity ions by the component of the electrostatic potential that is non-constant on the flux surface, that we denote by
![]() $\tilde{\unicode[STIX]{x1D711}}$
and that defines the component of the electric field that is tangent to the flux surface. Specifically, this tangential electric field produces a radial
$\tilde{\unicode[STIX]{x1D711}}$
and that defines the component of the electric field that is tangent to the flux surface. Specifically, this tangential electric field produces a radial
![]() $E\times B$
drift that advects impurities on the flux surface. The effect of
$E\times B$
drift that advects impurities on the flux surface. The effect of
![]() $\tilde{\unicode[STIX]{x1D711}}$
on impurity transport is larger for impurities with higher electric charge.
$\tilde{\unicode[STIX]{x1D711}}$
on impurity transport is larger for impurities with higher electric charge.
A previous step to the assessment of the impact of
![]() $\tilde{\unicode[STIX]{x1D711}}$
on radial impurity transport is the neoclassical calculation of
$\tilde{\unicode[STIX]{x1D711}}$
on radial impurity transport is the neoclassical calculation of
![]() $\tilde{\unicode[STIX]{x1D711}}$
itselfFootnote
2
, which has typically been ignored in standard neoclassical simulations. The modern codes EUTERPE (Kornilov et al.
Reference Kornilov, Kleiber and Hatzky2005) and SFINCS (Landreman et al.
Reference Landreman, Smith, Mollén and Helander2014) can compute it. In García-Regaña et al. (Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017), results of
$\tilde{\unicode[STIX]{x1D711}}$
itselfFootnote
2
, which has typically been ignored in standard neoclassical simulations. The modern codes EUTERPE (Kornilov et al.
Reference Kornilov, Kleiber and Hatzky2005) and SFINCS (Landreman et al.
Reference Landreman, Smith, Mollén and Helander2014) can compute it. In García-Regaña et al. (Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017), results of
![]() $\tilde{\unicode[STIX]{x1D711}}$
from both codes for different stellarators and plasma regimes are presented. These extended neoclassical models have started to be used to revisit some of the previous calculations of neoclassical impurity fluxes and have shown substantial deviations (with respect to codes that do not include the effect of
$\tilde{\unicode[STIX]{x1D711}}$
from both codes for different stellarators and plasma regimes are presented. These extended neoclassical models have started to be used to revisit some of the previous calculations of neoclassical impurity fluxes and have shown substantial deviations (with respect to codes that do not include the effect of
![]() $\tilde{\unicode[STIX]{x1D711}}$
) for some machines and plasma conditions (García-Regaña et al.
Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017; Mollén et al.
Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018). Recently, the strong effect of
$\tilde{\unicode[STIX]{x1D711}}$
) for some machines and plasma conditions (García-Regaña et al.
Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017; Mollén et al.
Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018). Recently, the strong effect of
![]() $\tilde{\unicode[STIX]{x1D711}}$
on the neoclassical transport of highly charged collisional impurities in stellarators has been analytically proven in (Calvo et al.
Reference Calvo, Parra, Velasco, Alonso and García-Regaña2018).
$\tilde{\unicode[STIX]{x1D711}}$
on the neoclassical transport of highly charged collisional impurities in stellarators has been analytically proven in (Calvo et al.
Reference Calvo, Parra, Velasco, Alonso and García-Regaña2018).
Given the relevance of correctly determining
![]() $\tilde{\unicode[STIX]{x1D711}}$
, it is important to understand the equations that have to be solved to calculate it, and to derive and discuss analytically some features of the solutions to these equations. In this paper we do so for main ions in the
$\tilde{\unicode[STIX]{x1D711}}$
, it is important to understand the equations that have to be solved to calculate it, and to derive and discuss analytically some features of the solutions to these equations. In this paper we do so for main ions in the
![]() $1/\unicode[STIX]{x1D708}$
,
$1/\unicode[STIX]{x1D708}$
,
![]() $\sqrt{\unicode[STIX]{x1D708}}$
and superbanana-plateau low collisionality regimes (see Mynick Reference Mynick1984 for estimations of the effect of
$\sqrt{\unicode[STIX]{x1D708}}$
and superbanana-plateau low collisionality regimes (see Mynick Reference Mynick1984 for estimations of the effect of
![]() $\tilde{\unicode[STIX]{x1D711}}$
on main ion transport in low collisionality regimes under some simplified assumptions). Low collisionality regimes are the pertinent ones for the main ions in the core of reactor-relevant stellarator plasmas and, in addition, in these regimes
$\tilde{\unicode[STIX]{x1D711}}$
on main ion transport in low collisionality regimes under some simplified assumptions). Low collisionality regimes are the pertinent ones for the main ions in the core of reactor-relevant stellarator plasmas and, in addition, in these regimes
![]() $\tilde{\unicode[STIX]{x1D711}}$
is large and has significant impact on impurity transport. We will carry out such analytical discussion by using the techniques and results of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), where we studied the radial neoclassical transport of low collisionality ions in stellarators close to omnigeneity. Omnigenous magnetic fields (Hall & McNamara Reference Hall and McNamara1975; Cary & Shasharina Reference Cary and Shasharina1997; Parra et al.
Reference Parra, Calvo, Helander and Landreman2015) are those for which the orbit-averaged radial magnetic drift vanishes for all trapped particles. Omnigenous stellarators can be said to be perfectly optimized from a neoclassical point of view, exhibiting transport levels similar to those of a tokamak. In Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), expansions in large aspect ratio were not considered. In this article, we expand in small inverse aspect ratio (in the end, all stellarators in operation today have large aspect ratio (Beidler et al.
Reference Beidler, Allmaier, Isaev, Kasilov, Kernbichler, Leitold, Maassberg, Mikkelsen, Murakami and Schmidt2011)). We will see that the large aspect ratio expansion introduces a number of subtleties.
$\tilde{\unicode[STIX]{x1D711}}$
is large and has significant impact on impurity transport. We will carry out such analytical discussion by using the techniques and results of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), where we studied the radial neoclassical transport of low collisionality ions in stellarators close to omnigeneity. Omnigenous magnetic fields (Hall & McNamara Reference Hall and McNamara1975; Cary & Shasharina Reference Cary and Shasharina1997; Parra et al.
Reference Parra, Calvo, Helander and Landreman2015) are those for which the orbit-averaged radial magnetic drift vanishes for all trapped particles. Omnigenous stellarators can be said to be perfectly optimized from a neoclassical point of view, exhibiting transport levels similar to those of a tokamak. In Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), expansions in large aspect ratio were not considered. In this article, we expand in small inverse aspect ratio (in the end, all stellarators in operation today have large aspect ratio (Beidler et al.
Reference Beidler, Allmaier, Isaev, Kasilov, Kernbichler, Leitold, Maassberg, Mikkelsen, Murakami and Schmidt2011)). We will see that the large aspect ratio expansion introduces a number of subtleties.
Let us emphasize that closeness to omnigeneity is not a mere academic requirement. It is well-known (Galeev & Sagdeev Reference Galeev, Sagdeev and Leontovich1979; Ho & Kulsrud Reference Ho and Kulsrud1987) that, for sufficiently low ion collisionality, tangential drifts have to be kept in the stellarator drift-kinetic equation. If the radial electric field is not small and the aspect ratio is large, one can show that the drift kinetic equation is radially local and that the tangential magnetic drift is negligible compared to the tangential
![]() $E\times B$
drift. But if one of these assumptions fails (that is, if the radial electric field is small or the stellarator is compact), the drift-kinetic equation becomes radially global (with obvious negative consequences for confinement, because then the radial excursion associated with a particle orbit can be as large as the stellarator minor radius) at small collisionality values unless the stellarator is close to omnigeneity. If the magnetic configuration is close to being omnigenous and the deviation from omnigeneity has small spatial gradients, the set of equations consisting of the drift-kinetic equation and the quasineutrality equation can be rigorously proven to be linear and radially local (Calvo et al.
Reference Calvo, Parra, Velasco and Alonso2017). Not only do the resulting equations include the effect of
$E\times B$
drift. But if one of these assumptions fails (that is, if the radial electric field is small or the stellarator is compact), the drift-kinetic equation becomes radially global (with obvious negative consequences for confinement, because then the radial excursion associated with a particle orbit can be as large as the stellarator minor radius) at small collisionality values unless the stellarator is close to omnigeneity. If the magnetic configuration is close to being omnigenous and the deviation from omnigeneity has small spatial gradients, the set of equations consisting of the drift-kinetic equation and the quasineutrality equation can be rigorously proven to be linear and radially local (Calvo et al.
Reference Calvo, Parra, Velasco and Alonso2017). Not only do the resulting equations include the effect of
![]() $\tilde{\unicode[STIX]{x1D711}}$
, but also the effect of the tangential magnetic drift. As we have pointed out, the tangential magnetic drift has to be taken into account to describe the transport of the main ions at very low collisionality in compact stellarators and in situations of small radial electric field even if the aspect ratio is large. The importance of the tangential magnetic drift in the latter case is a subject of active research (Matsuoka et al.
Reference Matsuoka, Satake, Kanno and Sugama2015). In this paper, we will pay special attention to the behaviour of
$\tilde{\unicode[STIX]{x1D711}}$
, but also the effect of the tangential magnetic drift. As we have pointed out, the tangential magnetic drift has to be taken into account to describe the transport of the main ions at very low collisionality in compact stellarators and in situations of small radial electric field even if the aspect ratio is large. The importance of the tangential magnetic drift in the latter case is a subject of active research (Matsuoka et al.
Reference Matsuoka, Satake, Kanno and Sugama2015). In this paper, we will pay special attention to the behaviour of
![]() $\tilde{\unicode[STIX]{x1D711}}$
in regimes where the tangential magnetic drift has to be retained.
$\tilde{\unicode[STIX]{x1D711}}$
in regimes where the tangential magnetic drift has to be retained.
Apart from discussing
![]() $\tilde{\unicode[STIX]{x1D711}}$
analytically in the
$\tilde{\unicode[STIX]{x1D711}}$
analytically in the
![]() $1/\unicode[STIX]{x1D708}$
,
$1/\unicode[STIX]{x1D708}$
,
![]() $\sqrt{\unicode[STIX]{x1D708}}$
or superbanana-plateau regimes, we will verify and illustrate the results by comparing them with KNOSOS (Velasco et al.
Reference Velasco, Calvo, García-Regaña, Parra, Satake and Alonso2018), a newly developed bounce-averaged code that solves the drift-kinetic and quasineutrality equations derived in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) (for the time being, KNOSOS uses a pitch-angle scattering collision operator), and therefore retains the tangential magnetic drift (among the two codes mentioned some paragraphs above, EUTERPE does not retain the tangential magnetic drift, whereas a way to try to retain it in SFINCS has been recently reported in Paul et al.
Reference Paul, Landreman, Poli, Spong, Smith and Dorland2017). Finally, a remark on the scope of this paper is in order. Whereas the expansion around omnigeneity should be considered as a realistic approach to the analysis of magnetic configurations that aspire to confine sufficiently well to be the basis of stellarator reactor designs, our present treatment is limited by the requirement of small gradients of the non-omnigenous perturbation in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). It would be important to address the relaxation of this condition in future research. Some ideas about the kind of complications introduced by large gradients can be found in Calvo et al. (Reference Calvo, Parra, Alonso and Velasco2014, Reference Calvo, Parra, Velasco and Alonso2015) in the setting of perturbed quasisymmetric configurations. Stellarators close to quasisymmetry, where the non-quasisymmetric perturbation has small gradients, were treated in detail in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2013). Finally, we note that a tokamak with (slightly) broken axisymmetry can be viewed as a particular case of a magnetic configuration close to omnigeneity, and therefore the tools and results of this paper can be directly applied to problems such as the calculation of tokamak neoclassical toroidal viscosity.
$\sqrt{\unicode[STIX]{x1D708}}$
or superbanana-plateau regimes, we will verify and illustrate the results by comparing them with KNOSOS (Velasco et al.
Reference Velasco, Calvo, García-Regaña, Parra, Satake and Alonso2018), a newly developed bounce-averaged code that solves the drift-kinetic and quasineutrality equations derived in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) (for the time being, KNOSOS uses a pitch-angle scattering collision operator), and therefore retains the tangential magnetic drift (among the two codes mentioned some paragraphs above, EUTERPE does not retain the tangential magnetic drift, whereas a way to try to retain it in SFINCS has been recently reported in Paul et al.
Reference Paul, Landreman, Poli, Spong, Smith and Dorland2017). Finally, a remark on the scope of this paper is in order. Whereas the expansion around omnigeneity should be considered as a realistic approach to the analysis of magnetic configurations that aspire to confine sufficiently well to be the basis of stellarator reactor designs, our present treatment is limited by the requirement of small gradients of the non-omnigenous perturbation in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). It would be important to address the relaxation of this condition in future research. Some ideas about the kind of complications introduced by large gradients can be found in Calvo et al. (Reference Calvo, Parra, Alonso and Velasco2014, Reference Calvo, Parra, Velasco and Alonso2015) in the setting of perturbed quasisymmetric configurations. Stellarators close to quasisymmetry, where the non-quasisymmetric perturbation has small gradients, were treated in detail in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2013). Finally, we note that a tokamak with (slightly) broken axisymmetry can be viewed as a particular case of a magnetic configuration close to omnigeneity, and therefore the tools and results of this paper can be directly applied to problems such as the calculation of tokamak neoclassical toroidal viscosity.
The rest of the paper is organized as follows. In § 2, after defining the coordinates that will be employed in the theoretical derivations (§ 2.1) and introducing the notion of omnigeneity (§ 2.2), we present in § 2.3 the neoclassical equations that determine
![]() $\tilde{\unicode[STIX]{x1D711}}$
in low collisionality regimes of stellarators close to omnigeneity when the deviation from omnigeneity has small spatial gradients. We will also see how
$\tilde{\unicode[STIX]{x1D711}}$
in low collisionality regimes of stellarators close to omnigeneity when the deviation from omnigeneity has small spatial gradients. We will also see how
![]() $\tilde{\unicode[STIX]{x1D711}}$
scales with the size of the deviation from omnigeneity. In § 2.4, and for large aspect ratio, the scaling with aspect ratio of some quantities entering the neoclassical equations is given; these expressions will be useful in later sections. In § 2.5, the magnetic field close to omnigeneity that we will use for the numerical examples is described. With this magnetic field, and taking reactor-relevant parameter values, in § 3 we give a plot (see figure 3) calculated by KNOSOS showing the dependence of the size of the non-constant component of the electrostatic potential on the collisionality and the radial electric field. The objective of the next section, § 4, is to explain mathematically the different regimes observed in plots like that in figure 3. Hence, in § 4 we discuss analytically the features of
$\tilde{\unicode[STIX]{x1D711}}$
scales with the size of the deviation from omnigeneity. In § 2.4, and for large aspect ratio, the scaling with aspect ratio of some quantities entering the neoclassical equations is given; these expressions will be useful in later sections. In § 2.5, the magnetic field close to omnigeneity that we will use for the numerical examples is described. With this magnetic field, and taking reactor-relevant parameter values, in § 3 we give a plot (see figure 3) calculated by KNOSOS showing the dependence of the size of the non-constant component of the electrostatic potential on the collisionality and the radial electric field. The objective of the next section, § 4, is to explain mathematically the different regimes observed in plots like that in figure 3. Hence, in § 4 we discuss analytically the features of
![]() $\tilde{\unicode[STIX]{x1D711}}$
in the
$\tilde{\unicode[STIX]{x1D711}}$
in the
![]() $1/\unicode[STIX]{x1D708}$
,
$1/\unicode[STIX]{x1D708}$
,
![]() $\sqrt{\unicode[STIX]{x1D708}}$
and superbanana-plateau asymptotic regimes as implied by the equations given in § 2.3 (as explained in Calvo et al.
Reference Calvo, Parra, Velasco and Alonso2017, those equations are not valid for lower collisionality regimes like the superbanana or
$\sqrt{\unicode[STIX]{x1D708}}$
and superbanana-plateau asymptotic regimes as implied by the equations given in § 2.3 (as explained in Calvo et al.
Reference Calvo, Parra, Velasco and Alonso2017, those equations are not valid for lower collisionality regimes like the superbanana or
![]() $\unicode[STIX]{x1D708}$
regimes, the essential reason being that for such low collisionality values one has to take into account the radial displacement of the trajectories). In particular, we will comment on the scaling of
$\unicode[STIX]{x1D708}$
regimes, the essential reason being that for such low collisionality values one has to take into account the radial displacement of the trajectories). In particular, we will comment on the scaling of
![]() $\tilde{\unicode[STIX]{x1D711}}$
with collisionality and aspect ratio, as well as on its behaviour under stellarator symmetry transformations. Detailed numerical checks of the analytical results with KNOSOS are provided throughout this section. Of course, assuming closeness to omnigeneity is not required if one is only interested in studying the
$\tilde{\unicode[STIX]{x1D711}}$
with collisionality and aspect ratio, as well as on its behaviour under stellarator symmetry transformations. Detailed numerical checks of the analytical results with KNOSOS are provided throughout this section. Of course, assuming closeness to omnigeneity is not required if one is only interested in studying the
![]() $1/\unicode[STIX]{x1D708}$
and
$1/\unicode[STIX]{x1D708}$
and
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regimes (the former exists in any stellarator and the latter exists in large aspect ratio stellarators with non-small radial electric field), but the assumption is necessary to be able to study, in the same framework, those two collisionality regimes together with the superbanana-plateau regime. In § 5, we give the conclusions. In particular, table 1 condenses the main analytical results derived in the paper. Finally, we point out that, for simplicity, throughout the paper we assume that the electrons are adiabatic. This is a good approximation in many cases, but its accuracy certainly depends on the particular collisionality regimes in which the main ions and the electrons are, and situations in which the electrons have to be treated kinetically are not uncommon (see e.g. Velasco et al.
Reference Velasco, Calvo, Satake, Alonso, Nunami, Yokoyama, Sato, Estrada, Fontdecaba and Liniers2017, García-Regaña et al.
Reference García-Regaña, Estrada, Calvo, Velasco, Alonso, Carralero, Kleiber, Landreman, Mollén and Sánchez2018). In these situations, a kinetic treatment of the electrons is also needed to calculate
$\sqrt{\unicode[STIX]{x1D708}}$
regimes (the former exists in any stellarator and the latter exists in large aspect ratio stellarators with non-small radial electric field), but the assumption is necessary to be able to study, in the same framework, those two collisionality regimes together with the superbanana-plateau regime. In § 5, we give the conclusions. In particular, table 1 condenses the main analytical results derived in the paper. Finally, we point out that, for simplicity, throughout the paper we assume that the electrons are adiabatic. This is a good approximation in many cases, but its accuracy certainly depends on the particular collisionality regimes in which the main ions and the electrons are, and situations in which the electrons have to be treated kinetically are not uncommon (see e.g. Velasco et al.
Reference Velasco, Calvo, Satake, Alonso, Nunami, Yokoyama, Sato, Estrada, Fontdecaba and Liniers2017, García-Regaña et al.
Reference García-Regaña, Estrada, Calvo, Velasco, Alonso, Carralero, Kleiber, Landreman, Mollén and Sánchez2018). In these situations, a kinetic treatment of the electrons is also needed to calculate
![]() $\tilde{\unicode[STIX]{x1D711}}$
.
$\tilde{\unicode[STIX]{x1D711}}$
.
2 Low collisionality neoclassical equations in stellarators close to omnigeneity
2.1 Phase space coordinates
In the kinetic description of low collisionality regimes, it is useful to employ spatial coordinates
![]() $\{r,\unicode[STIX]{x1D6FC},l\}$
, defined as follows. The radial coordinate
$\{r,\unicode[STIX]{x1D6FC},l\}$
, defined as follows. The radial coordinate
![]() $r\in [0,a]$
labels the magnetic surface and has dimensions of length,
$r\in [0,a]$
labels the magnetic surface and has dimensions of length,
![]() $a$
being the minor radius of the stellarator. For given
$a$
being the minor radius of the stellarator. For given
![]() $r$
, the angular coordinate
$r$
, the angular coordinate
![]() $\unicode[STIX]{x1D6FC}\in [0,2\unicode[STIX]{x03C0})$
selects a magnetic field line on the surface. The coordinate
$\unicode[STIX]{x1D6FC}\in [0,2\unicode[STIX]{x03C0})$
selects a magnetic field line on the surface. The coordinate
![]() $l\in [0,l_{\text{max}}(r,\unicode[STIX]{x1D6FC}))$
is the arc length along the field line. In these coordinates the magnetic field reads
$l\in [0,l_{\text{max}}(r,\unicode[STIX]{x1D6FC}))$
is the arc length along the field line. In these coordinates the magnetic field reads
As for the meaning of the flux function
![]() $\unicode[STIX]{x1D6F9}(r)$
, it is easy to check that
$\unicode[STIX]{x1D6F9}(r)$
, it is easy to check that
![]() $2\unicode[STIX]{x03C0}\int _{0}^{r_{0}}\unicode[STIX]{x1D6F9}(r)\,\text{d}r$
equals the magnetic flux across a surface defined by
$2\unicode[STIX]{x03C0}\int _{0}^{r_{0}}\unicode[STIX]{x1D6F9}(r)\,\text{d}r$
equals the magnetic flux across a surface defined by
![]() $l=\text{const.}$
and
$l=\text{const.}$
and
![]() $0\leqslant r\leqslant r_{0}$
.
$0\leqslant r\leqslant r_{0}$
.
In these coordinates the flux-surface average of a function
![]() $f(r,\unicode[STIX]{x1D6FC},l)$
is defined as
$f(r,\unicode[STIX]{x1D6FC},l)$
is defined as
where
![]() $\unicode[STIX]{x1D6F9}B^{-1}=[(\unicode[STIX]{x1D735}r\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC})\boldsymbol{\cdot }\unicode[STIX]{x1D735}l]^{-1}$
is the volume element (the coordinates
$\unicode[STIX]{x1D6F9}B^{-1}=[(\unicode[STIX]{x1D735}r\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC})\boldsymbol{\cdot }\unicode[STIX]{x1D735}l]^{-1}$
is the volume element (the coordinates
![]() $\{r,\unicode[STIX]{x1D6FC},l\}$
are chosen such that
$\{r,\unicode[STIX]{x1D6FC},l\}$
are chosen such that
![]() $\unicode[STIX]{x1D6F9}>0$
),
$\unicode[STIX]{x1D6F9}>0$
),
![]() $B(r,\unicode[STIX]{x1D6FC},l)$
is the magnitude of
$B(r,\unicode[STIX]{x1D6FC},l)$
is the magnitude of
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
with
![]() $V(r)$
being the volume enclosed by the surface
$V(r)$
being the volume enclosed by the surface
![]() $r$
. We will use primes to denote differentiation with respect to
$r$
. We will use primes to denote differentiation with respect to
![]() $r$
.
$r$
.
In velocity space, we employ coordinates
![]() $\{v,\unicode[STIX]{x1D706},\unicode[STIX]{x1D70E}\}$
, where
$\{v,\unicode[STIX]{x1D706},\unicode[STIX]{x1D70E}\}$
, where
![]() $v$
is the magnitude of the velocity
$v$
is the magnitude of the velocity
![]() $\boldsymbol{v}$
,
$\boldsymbol{v}$
,
![]() $\unicode[STIX]{x1D706}=v_{\bot }^{2}/(Bv^{2})$
is the pitch-angle coordinate,
$\unicode[STIX]{x1D706}=v_{\bot }^{2}/(Bv^{2})$
is the pitch-angle coordinate,
![]() $v_{\bot }$
is the component of
$v_{\bot }$
is the component of
![]() $\boldsymbol{v}$
perpendicular to
$\boldsymbol{v}$
perpendicular to
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
![]() $\unicode[STIX]{x1D70E}=v_{\Vert }/|v_{\Vert }|$
is the sign of the parallel velocity, with
$\unicode[STIX]{x1D70E}=v_{\Vert }/|v_{\Vert }|$
is the sign of the parallel velocity, with
Integrals over velocity space of gyrophase-independent functions (all functions in this paper are independent of gyrophase) read, in these coordinates,
2.2 Perturbed omnigenous magnetic fields
Trapped trajectories are those with
![]() $\unicode[STIX]{x1D706}\in [B_{\text{max}}^{-1},B_{\text{min}}^{-1}]$
, where
$\unicode[STIX]{x1D706}\in [B_{\text{max}}^{-1},B_{\text{min}}^{-1}]$
, where
![]() $B_{\text{max}}(r)$
and
$B_{\text{max}}(r)$
and
![]() $B_{\text{min}}(r)$
are, respectively, the maximum and minimum values of
$B_{\text{min}}(r)$
are, respectively, the maximum and minimum values of
![]() $B$
on the flux surface. For each trapped trajectory, the second adiabatic invariant reads
$B$
on the flux surface. For each trapped trajectory, the second adiabatic invariant reads
Here,
![]() $l_{b_{1}}$
and
$l_{b_{1}}$
and
![]() $l_{b_{2}}$
are the bounce points of the trapped orbit, obtained by solving in
$l_{b_{2}}$
are the bounce points of the trapped orbit, obtained by solving in
![]() $l$
the equation
$l$
the equation
![]() $1-\unicode[STIX]{x1D706}B(r,\unicode[STIX]{x1D6FC},l)=0$
(see figure 1 for a cartoon showing some of the quantities that describe trapped trajectories).
$1-\unicode[STIX]{x1D706}B(r,\unicode[STIX]{x1D6FC},l)=0$
(see figure 1 for a cartoon showing some of the quantities that describe trapped trajectories).

Figure 1. Cartoon showing some of the quantities (defined in the text) employed to describe a trapped trajectory.
The importance of
![]() $J$
comes from the relations
$J$
comes from the relations
where
is the magnetic drift,
![]() $\hat{\boldsymbol{b}}=B^{-1}\boldsymbol{B}$
,
$\hat{\boldsymbol{b}}=B^{-1}\boldsymbol{B}$
,
![]() $m$
is the particle mass,
$m$
is the particle mass,
![]() $Ze$
is the particle charge (we assume
$Ze$
is the particle charge (we assume
![]() $Z\sim 1$
),
$Z\sim 1$
),
![]() $e$
is the proton charge and
$e$
is the proton charge and
is the bounce time; i.e. the time that the trapped particle needs to complete its orbit. Hence,
![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}J$
and
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}J$
and
![]() $\unicode[STIX]{x2202}_{r}J$
contain the information on the motion of the trapped particle in the directions perpendicular to
$\unicode[STIX]{x2202}_{r}J$
contain the information on the motion of the trapped particle in the directions perpendicular to
![]() $\boldsymbol{B}$
, averaged over the motion in the direction parallel to
$\boldsymbol{B}$
, averaged over the motion in the direction parallel to
![]() $\boldsymbol{B}$
.
$\boldsymbol{B}$
.
The magnetic field is called omnigenous (Cary & Shasharina Reference Cary and Shasharina1997; Parra et al.
Reference Parra, Calvo, Helander and Landreman2015) if the average radial magnetic drift vanishes for all trapped particles. Due to (2.7), this is equivalent to saying that the second adiabatic invariant is independent of
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}J=0$
, for all trapped trajectories.
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}J=0$
, for all trapped trajectories.
From the definition of omnigeneity one can deduce that, for any function
![]() $q$
that depends on
$q$
that depends on
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $l$
only through an omnigenous magnetic field
$l$
only through an omnigenous magnetic field
![]() $B$
, one has (Cary & Shasharina Reference Cary and Shasharina1997; Helander & Nührenberg Reference Helander and Nührenberg2009; Calvo et al.
Reference Calvo, Parra, Velasco and Alonso2017)
$B$
, one has (Cary & Shasharina Reference Cary and Shasharina1997; Helander & Nührenberg Reference Helander and Nührenberg2009; Calvo et al.
Reference Calvo, Parra, Velasco and Alonso2017)
This useful property is employed in the derivation of the neoclassical equations of § 2.3 and it will also be used in the analysis of their solutions.
In this paper, we will carry out the calculations in magnetic configurations that can be written as an exactly omnigenous magnetic field
![]() $\boldsymbol{B}_{0}$
plus a perturbation
$\boldsymbol{B}_{0}$
plus a perturbation
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}_{1}$
,
$\unicode[STIX]{x1D6FF}\boldsymbol{B}_{1}$
,
where
![]() $B_{0}:=|\boldsymbol{B}_{0}|\sim |\boldsymbol{B}_{1}|=:B_{1}$
and
$B_{0}:=|\boldsymbol{B}_{0}|\sim |\boldsymbol{B}_{1}|=:B_{1}$
and
![]() $0\leqslant \unicode[STIX]{x1D6FF}\ll 1$
. As advanced in § 1, and following Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), we restrict ourselves to cases in which the characteristic scale of variation of
$0\leqslant \unicode[STIX]{x1D6FF}\ll 1$
. As advanced in § 1, and following Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), we restrict ourselves to cases in which the characteristic scale of variation of
![]() $B_{1}$
on the flux surface is not much smaller than that of
$B_{1}$
on the flux surface is not much smaller than that of
![]() $B_{0}$
. Specifically, we require
$B_{0}$
. Specifically, we require
![]() $|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}B_{1}|/|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}B_{0}|\sim |\unicode[STIX]{x2202}_{l}B_{1}|/|\unicode[STIX]{x2202}_{l}B_{0}|\ll \unicode[STIX]{x1D6FF}^{-1}$
. Thus, in terms of an expansion in
$|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}B_{1}|/|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}B_{0}|\sim |\unicode[STIX]{x2202}_{l}B_{1}|/|\unicode[STIX]{x2202}_{l}B_{0}|\ll \unicode[STIX]{x1D6FF}^{-1}$
. Thus, in terms of an expansion in
![]() $\unicode[STIX]{x1D6FF}\ll 1$
, we can assume that
$\unicode[STIX]{x1D6FF}\ll 1$
, we can assume that
![]() $B_{0}$
and
$B_{0}$
and
![]() $B_{1}$
have a similar characteristic variation length on the flux surface, that we can take to be
$B_{1}$
have a similar characteristic variation length on the flux surface, that we can take to be
![]() $R_{0}$
, the major radius of the stellarator. This is what we mean when we say that the deviation from omnigeneity has small gradients. In particular, deviations with small gradients can deform the omnigenous magnetic wells, but not create new wells.
$R_{0}$
, the major radius of the stellarator. This is what we mean when we say that the deviation from omnigeneity has small gradients. In particular, deviations with small gradients can deform the omnigenous magnetic wells, but not create new wells.
2.3 Drift-kinetic and quasineutrality equations in stellarators close to omnigeneity
In drift kinetics (Hazeltine Reference Hazeltine1973; Parra & Calvo Reference Parra and Calvo2011; Calvo et al.
Reference Calvo, Parra, Velasco and Alonso2013), the characteristic frequency of particle motion in the direction parallel to
![]() $\boldsymbol{B}$
is
$\boldsymbol{B}$
is
![]() $O(v_{t}/R_{0})$
, whereas the motion perpendicular to the magnetic field has a much smaller typical frequency
$O(v_{t}/R_{0})$
, whereas the motion perpendicular to the magnetic field has a much smaller typical frequency
![]() $O(\unicode[STIX]{x1D70C}_{\ast }v_{t}/R_{0})$
, where
$O(\unicode[STIX]{x1D70C}_{\ast }v_{t}/R_{0})$
, where
![]() $\unicode[STIX]{x1D70C}_{\ast }=\unicode[STIX]{x1D70C}/R_{0}\ll 1$
is the normalized Larmor radius, with
$\unicode[STIX]{x1D70C}_{\ast }=\unicode[STIX]{x1D70C}/R_{0}\ll 1$
is the normalized Larmor radius, with
![]() $\unicode[STIX]{x1D70C}=v_{t}/\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D70C}=v_{t}/\unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D6FA}=ZeB/m$
. Low collisionality regimesFootnote
3
are defined by
$\unicode[STIX]{x1D6FA}=ZeB/m$
. Low collisionality regimesFootnote
3
are defined by
![]() $\unicode[STIX]{x1D708}_{\ast }\ll 1$
, where
$\unicode[STIX]{x1D708}_{\ast }\ll 1$
, where
![]() $\unicode[STIX]{x1D708}_{\ast }=\unicode[STIX]{x1D708}_{ii}R_{0}/v_{t}$
is the ion collisionality,
$\unicode[STIX]{x1D708}_{\ast }=\unicode[STIX]{x1D708}_{ii}R_{0}/v_{t}$
is the ion collisionality,
![]() $\unicode[STIX]{x1D708}_{ii}$
is the ion–ion collision frequency and
$\unicode[STIX]{x1D708}_{ii}$
is the ion–ion collision frequency and
![]() $v_{t}=\sqrt{T/m}$
is the ion thermal speed. The condition
$v_{t}=\sqrt{T/m}$
is the ion thermal speed. The condition
![]() $\unicode[STIX]{x1D708}_{\ast }\ll 1$
means that the characteristic parallel streaming frequency is much greater than the collision frequency
$\unicode[STIX]{x1D708}_{\ast }\ll 1$
means that the characteristic parallel streaming frequency is much greater than the collision frequency
![]() $\unicode[STIX]{x1D708}_{ii}$
, and therefore the drift-kinetic ion equation can be averaged over the parallel motion. In this subsection, we give the neoclassical equations for low collisionality plasmas in stellarators close to omnigeneity where the deviation from omnigeneity has small gradients, but we do not include their derivation. For that, we refer the reader to Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). No assumptions are made about the aspect ratio of the stellarator yet.
$\unicode[STIX]{x1D708}_{ii}$
, and therefore the drift-kinetic ion equation can be averaged over the parallel motion. In this subsection, we give the neoclassical equations for low collisionality plasmas in stellarators close to omnigeneity where the deviation from omnigeneity has small gradients, but we do not include their derivation. For that, we refer the reader to Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017). No assumptions are made about the aspect ratio of the stellarator yet.
For
![]() $\unicode[STIX]{x1D6FF}\ll 1$
, one finds that the electrostatic potential,
$\unicode[STIX]{x1D6FF}\ll 1$
, one finds that the electrostatic potential,
![]() $\unicode[STIX]{x1D711}$
, is a flux function to lowest order,
$\unicode[STIX]{x1D711}$
, is a flux function to lowest order,
The component of the electrostatic potential that is non-constant on the flux surface, denoted in § 1 by
![]() $\tilde{\unicode[STIX]{x1D711}}$
, is therefore given by
$\tilde{\unicode[STIX]{x1D711}}$
, is therefore given by
In an expansion in
![]() $\unicode[STIX]{x1D6FF}$
, the ion distribution function,
$\unicode[STIX]{x1D6FF}$
, the ion distribution function,
![]() $F$
, can be written as
$F$
, can be written as
where
![]() $F_{M}$
is a Maxwellian distribution constant on flux surfaces,
$F_{M}$
is a Maxwellian distribution constant on flux surfaces,
and
![]() $n$
and
$n$
and
![]() $T$
are the ion density and temperature. The non-adiabatic perturbation to the Maxwellian distribution,
$T$
are the ion density and temperature. The non-adiabatic perturbation to the Maxwellian distribution,
![]() $g^{(1)}(r,\unicode[STIX]{x1D6FC},l,v,\unicode[STIX]{x1D706})$
, is independent of
$g^{(1)}(r,\unicode[STIX]{x1D6FC},l,v,\unicode[STIX]{x1D706})$
, is independent of
![]() $l$
and
$l$
and
![]() $\unicode[STIX]{x1D70E}$
, and vanishes for passing trajectories of the omnigenous field,
$\unicode[STIX]{x1D70E}$
, and vanishes for passing trajectories of the omnigenous field,
![]() $0\leqslant \unicode[STIX]{x1D706}<B_{0,\text{max}}^{-1}$
, where
$0\leqslant \unicode[STIX]{x1D706}<B_{0,\text{max}}^{-1}$
, where
![]() $B_{0,\text{max}}(r)$
is the maximum value of
$B_{0,\text{max}}(r)$
is the maximum value of
![]() $B_{0}$
on the flux surface. The function
$B_{0}$
on the flux surface. The function
![]() $g^{(1)}$
can be chosen such that
$g^{(1)}$
can be chosen such that
The equations that determine
![]() $g^{(1)}$
and
$g^{(1)}$
and
![]() $\unicode[STIX]{x1D711}^{(1)}$
are radially local and linear. First, one has the bounce-averaged drift-kinetic equation for trapped trajectories,
$\unicode[STIX]{x1D711}^{(1)}$
are radially local and linear. First, one has the bounce-averaged drift-kinetic equation for trapped trajectories,
whereFootnote 4
and
![]() $C_{ii}^{\ell }$
is the linearized ion–ion collision operator (Helander & Sigmar Reference Helander, Sigmar and Haines2002). The ion–electron collision term has been neglected because we assume
$C_{ii}^{\ell }$
is the linearized ion–ion collision operator (Helander & Sigmar Reference Helander, Sigmar and Haines2002). The ion–electron collision term has been neglected because we assume
![]() $\sqrt{m_{e}/m}\ll 1$
, with
$\sqrt{m_{e}/m}\ll 1$
, with
![]() $m_{e}$
the electron mass. The superindex
$m_{e}$
the electron mass. The superindex
![]() $(0)$
in
$(0)$
in
![]() $C_{ii}^{\ell (0)}$
means that
$C_{ii}^{\ell (0)}$
means that
![]() $B$
has been replaced by
$B$
has been replaced by
![]() $B_{0}$
in the expression for the collision operator in coordinates
$B_{0}$
in the expression for the collision operator in coordinates
![]() $v$
and
$v$
and
![]() $\unicode[STIX]{x1D706}$
. Analogously,
$\unicode[STIX]{x1D706}$
. Analogously,
and
![]() $l_{b_{10}}$
,
$l_{b_{10}}$
,
![]() $l_{b_{20}}$
are the solutions of the equation
$l_{b_{20}}$
are the solutions of the equation
![]() $1-\unicode[STIX]{x1D706}B_{0}(r,\unicode[STIX]{x1D6FC},l)=0$
for
$1-\unicode[STIX]{x1D706}B_{0}(r,\unicode[STIX]{x1D6FC},l)=0$
for
![]() $\unicode[STIX]{x1D706}\geqslant B_{0,\text{max}}^{-1}$
. Finally, note that
$\unicode[STIX]{x1D706}\geqslant B_{0,\text{max}}^{-1}$
. Finally, note that
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}$
does not depend on
$\unicode[STIX]{x2202}_{r}J^{(0)}$
does not depend on
![]() $\unicode[STIX]{x1D6FC}$
because
$\unicode[STIX]{x1D6FC}$
because
![]() $B_{0}$
is omnigenous. Sometimes, it will be useful to write
$B_{0}$
is omnigenous. Sometimes, it will be useful to write
![]() $J^{(1)}=J_{B}^{(1)}+J_{\unicode[STIX]{x1D711}}^{(1)}$
, where
$J^{(1)}=J_{B}^{(1)}+J_{\unicode[STIX]{x1D711}}^{(1)}$
, where
and
Second, one has the quasineutrality equation. In the mass ratio expansion
![]() $\sqrt{m_{e}/m}$
$\sqrt{m_{e}/m}$
![]() $\ll 1$
, the non-adiabatic response of the electrons can be dropped, giving
$\ll 1$
, the non-adiabatic response of the electrons can be dropped, giving
where
![]() $T_{e}(r)$
is the electron temperature. Note that the choice (2.17) implies that
$T_{e}(r)$
is the electron temperature. Note that the choice (2.17) implies that
where the flux-surface average is taken using
![]() $B_{0}$
. In addition, integration of (2.25) over trapped orbits, application of property (2.11) and of condition (2.17) implies
$B_{0}$
. In addition, integration of (2.25) over trapped orbits, application of property (2.11) and of condition (2.17) implies
Equations (2.18) and (2.25) are correct for values of the collisionality that include the neoclassical transport regimes known as
![]() $1/\unicode[STIX]{x1D708}$
,
$1/\unicode[STIX]{x1D708}$
,
![]() $\sqrt{\unicode[STIX]{x1D708}}$
and superbanana-plateau regimes. In Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), it was explained why the equations stop to be valid at low enough values of the collisionality, so that they should be modified in case one is interested in describing, for example, the
$\sqrt{\unicode[STIX]{x1D708}}$
and superbanana-plateau regimes. In Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), it was explained why the equations stop to be valid at low enough values of the collisionality, so that they should be modified in case one is interested in describing, for example, the
![]() $\unicode[STIX]{x1D708}$
or superbanana regimes. In § 2.4, we explain how some of the quantities entering the neoclassical equations (2.18) and (2.25) behave when a large aspect ratio expansion is taken. In § 2.5, the perturbed omnigenous magnetic field that will be later used in the numerical examples is described.
$\unicode[STIX]{x1D708}$
or superbanana regimes. In § 2.4, we explain how some of the quantities entering the neoclassical equations (2.18) and (2.25) behave when a large aspect ratio expansion is taken. In § 2.5, the perturbed omnigenous magnetic field that will be later used in the numerical examples is described.
2.4 Conventions and some useful scalings for large aspect ratio stellarators
Stellarators in operation today have large aspect ratios,
![]() $\unicode[STIX]{x1D716}^{-1}=R_{0}/a$
. In Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), the scaling with
$\unicode[STIX]{x1D716}^{-1}=R_{0}/a$
. In Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), the scaling with
![]() $\unicode[STIX]{x1D716}\ll 1$
was not determined, and we would like to address this refinement in the present paper. In this subsection, some conventions that are convenient for
$\unicode[STIX]{x1D716}\ll 1$
was not determined, and we would like to address this refinement in the present paper. In this subsection, some conventions that are convenient for
![]() $\unicode[STIX]{x1D716}\ll 1$
are explained, and the scaling with
$\unicode[STIX]{x1D716}\ll 1$
are explained, and the scaling with
![]() $\unicode[STIX]{x1D716}$
of several quantities entering (2.18) and (2.25) is provided for later use.
$\unicode[STIX]{x1D716}$
of several quantities entering (2.18) and (2.25) is provided for later use.
In a given flux surface, we write magnetic fields in large aspect ratio stellarators close to omnigeneity as
where
![]() $B_{00}$
is constant and
$B_{00}$
is constant and
![]() $\tilde{B}_{0}\sim \unicode[STIX]{x1D716}B_{00}$
. As for the non-omnigenous perturbation, we assume
$\tilde{B}_{0}\sim \unicode[STIX]{x1D716}B_{00}$
. As for the non-omnigenous perturbation, we assume
![]() $B_{1}\sim \unicode[STIX]{x1D716}B_{00}$
. Note that if the aspect ratio is large, the meaningful measure of the size of the non-omnigenous perturbation is given by
$B_{1}\sim \unicode[STIX]{x1D716}B_{00}$
. Note that if the aspect ratio is large, the meaningful measure of the size of the non-omnigenous perturbation is given by
![]() $\unicode[STIX]{x1D6FF}\sim |B-B_{0}|/|B_{0}-B_{00}|$
. This is why we have included a factor
$\unicode[STIX]{x1D6FF}\sim |B-B_{0}|/|B_{0}-B_{00}|$
. This is why we have included a factor
![]() $\unicode[STIX]{x1D716}$
in our convention for the size of
$\unicode[STIX]{x1D716}$
in our convention for the size of
![]() $B_{1}$
. The definition
$B_{1}$
. The definition
is valid both for large aspect ratio,
![]() $\unicode[STIX]{x1D716}\ll 1$
, and tight aspect ratio,
$\unicode[STIX]{x1D716}\ll 1$
, and tight aspect ratio,
![]() $\unicode[STIX]{x1D716}\sim 1$
.
$\unicode[STIX]{x1D716}\sim 1$
.
The radial derivative of
![]() $B_{0}$
at the surface of interest will also be needed. In our models, we will assume
$B_{0}$
at the surface of interest will also be needed. In our models, we will assume
We proceed to explain how different quantities appearing in the neoclassical equations scale with
![]() $\unicode[STIX]{x1D716}$
. We denote by
$\unicode[STIX]{x1D716}$
. We denote by
![]() $\unicode[STIX]{x1D6E5}_{\text{trapped}}$
the size (measured in the coordinate
$\unicode[STIX]{x1D6E5}_{\text{trapped}}$
the size (measured in the coordinate
![]() $\unicode[STIX]{x1D706}$
) of the region of phase space corresponding to particles trapped in
$\unicode[STIX]{x1D706}$
) of the region of phase space corresponding to particles trapped in
![]() $B_{0}$
. Observing that the difference between the maximum and the minimum values of
$B_{0}$
. Observing that the difference between the maximum and the minimum values of
![]() $B_{0}$
on the flux surface is
$B_{0}$
on the flux surface is
![]() $O(\unicode[STIX]{x1D716}B_{00})$
, we infer that
$O(\unicode[STIX]{x1D716}B_{00})$
, we infer that
Analogous reasons lead to conclude that the size of the parallel velocity for trapped particles is
The scaling of
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}$
depends on the size of the radial electric field, obtained by imposing ambipolarity of the neoclassical radial particle fluxes. For typical values
$\unicode[STIX]{x2202}_{r}J^{(0)}$
depends on the size of the radial electric field, obtained by imposing ambipolarity of the neoclassical radial particle fluxes. For typical values
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }\sim \unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
, the term containing the radial electric field dominates and
$\unicode[STIX]{x1D711}_{0}^{\prime }\sim \unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
, the term containing the radial electric field dominates and
where we have assumed that the typical length of the omnigenous wells is
![]() $R_{0}$
. If the radial electric field is small,
$R_{0}$
. If the radial electric field is small,
![]() $|\unicode[STIX]{x1D711}_{0}^{\prime }|\lesssim T/(eR_{0})$
, thenFootnote
5
$|\unicode[STIX]{x1D711}_{0}^{\prime }|\lesssim T/(eR_{0})$
, thenFootnote
5
As for
![]() $J^{(1)}$
, we have
$J^{(1)}$
, we have
whereas
Recall that
![]() $\unicode[STIX]{x1D711}^{(1)}$
is one of the unknowns of the neoclassical equations and its size is to be determined.
$\unicode[STIX]{x1D711}^{(1)}$
is one of the unknowns of the neoclassical equations and its size is to be determined.
The function
![]() $\unicode[STIX]{x1D6F9}$
appearing in (2.1) scales as
$\unicode[STIX]{x1D6F9}$
appearing in (2.1) scales as
Regarding the plasma profile gradients, it is expected that, generically,
In large aspect ratio stellarators, the collision term on the right-hand side of (2.18) is dominated by the pitch-angle scattering piece of the collision operator,
where
is the ion–ion collision frequency,
![]() $\ln \unicode[STIX]{x1D6EC}$
is the Coulomb logarithm,
$\ln \unicode[STIX]{x1D6EC}$
is the Coulomb logarithm,
![]() $\unicode[STIX]{x1D700}_{0}$
is the vacuum permittivity,
$\unicode[STIX]{x1D700}_{0}$
is the vacuum permittivity,
and
Employing the estimates above for the scaling of
![]() $\unicode[STIX]{x1D6E5}_{\text{trapped}}$
and
$\unicode[STIX]{x1D6E5}_{\text{trapped}}$
and
![]() $v_{\Vert }^{(0)}$
with
$v_{\Vert }^{(0)}$
with
![]() $\unicode[STIX]{x1D716}$
, we find
$\unicode[STIX]{x1D716}$
, we find
which is the typical size of the collision term across the trapped region. It is important to realize that the condition for low collisionality ions, that reads
![]() $\unicode[STIX]{x1D708}_{\ast }\ll 1$
for
$\unicode[STIX]{x1D708}_{\ast }\ll 1$
for
![]() $\unicode[STIX]{x1D716}\sim 1$
, becomesFootnote
6
$\unicode[STIX]{x1D716}\sim 1$
, becomesFootnote
6
![]() $\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D716}^{3/2}$
for
$\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D716}^{3/2}$
for
![]() $\unicode[STIX]{x1D716}\ll 1$
. This result is derived by comparing the factor in front of
$\unicode[STIX]{x1D716}\ll 1$
. This result is derived by comparing the factor in front of
![]() $g^{(1)}$
on the right-hand side of (2.45) with the typical frequency of the parallel particle motion, which is
$g^{(1)}$
on the right-hand side of (2.45) with the typical frequency of the parallel particle motion, which is
![]() $O(\unicode[STIX]{x1D716}^{1/2}v_{t}/R_{0})$
when
$O(\unicode[STIX]{x1D716}^{1/2}v_{t}/R_{0})$
when
![]() $\unicode[STIX]{x1D716}\ll 1$
.
$\unicode[STIX]{x1D716}\ll 1$
.
Finally, we point out that (see (2.40)), when
![]() $\unicode[STIX]{x1D716}\ll 1$
, we can define
$\unicode[STIX]{x1D716}\ll 1$
, we can define
as the expression for the collisionality and
for the normalized Larmor radius.
2.5 Model magnetic field close to omnigeneity
In order to define a specific omnigenous field
![]() $B_{0}$
for the numerical examples provided in subsequent sections, we follow Cary & Shasharina (Reference Cary and Shasharina1997) and Landreman & Catto (Reference Landreman and Catto2012). The description is easier in Boozer coordinates (Boozer Reference Boozer1981). We denote by
$B_{0}$
for the numerical examples provided in subsequent sections, we follow Cary & Shasharina (Reference Cary and Shasharina1997) and Landreman & Catto (Reference Landreman and Catto2012). The description is easier in Boozer coordinates (Boozer Reference Boozer1981). We denote by
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D701}$
the poloidal and toroidal Boozer angles, respectively. We use the construction explained in section V of Landreman & Catto (Reference Landreman and Catto2012) with
$\unicode[STIX]{x1D701}$
the poloidal and toroidal Boozer angles, respectively. We use the construction explained in section V of Landreman & Catto (Reference Landreman and Catto2012) with
![]() $M=1$
and
$M=1$
and
![]() $N=4$
(which means that the contours of
$N=4$
(which means that the contours of
![]() $B_{0}$
close on themselves after 4 poloidal turns and 1 toroidal turn) and with rotational transform
$B_{0}$
close on themselves after 4 poloidal turns and 1 toroidal turn) and with rotational transform ![]() .We takeFootnote
7
.We takeFootnote
7
where the function
![]() $\unicode[STIX]{x1D702}$
is obtained as in equation (73) of Landreman & Catto (Reference Landreman and Catto2012). In figure 2 we show a plot of an omnigenous magnetic field of the form just introduced.
$\unicode[STIX]{x1D702}$
is obtained as in equation (73) of Landreman & Catto (Reference Landreman and Catto2012). In figure 2 we show a plot of an omnigenous magnetic field of the form just introduced.
As for the non-omnigenous perturbation, we take
Note that
![]() $B=B_{0}+\unicode[STIX]{x1D6FF}B_{1}$
is symmetric under the transformation
$B=B_{0}+\unicode[STIX]{x1D6FF}B_{1}$
is symmetric under the transformation
![]() $(\unicode[STIX]{x1D703},\unicode[STIX]{x1D701})\mapsto (-\unicode[STIX]{x1D703},-\unicode[STIX]{x1D701})$
. Magnetic fields with this property are called stellarator symmetric (Dewar & Hudson Reference Dewar and Hudson1998). Stellarator designs typically impose this symmetry on the magnetic configuration, and from here on we always assume that our magnetic field satisfies this.
$(\unicode[STIX]{x1D703},\unicode[STIX]{x1D701})\mapsto (-\unicode[STIX]{x1D703},-\unicode[STIX]{x1D701})$
. Magnetic fields with this property are called stellarator symmetric (Dewar & Hudson Reference Dewar and Hudson1998). Stellarator designs typically impose this symmetry on the magnetic configuration, and from here on we always assume that our magnetic field satisfies this.
Given Boozer angles
![]() $\{\unicode[STIX]{x1D703},\unicode[STIX]{x1D701}\}$
, there are many different ways to define coordinates
$\{\unicode[STIX]{x1D703},\unicode[STIX]{x1D701}\}$
, there are many different ways to define coordinates
![]() $\{\unicode[STIX]{x1D6FC},l\}$
. First, one has to choose a closed curve
$\{\unicode[STIX]{x1D6FC},l\}$
. First, one has to choose a closed curve
![]() ${\mathcal{C}}$
that is not contractible to a point. A simple choice is to take the curve
${\mathcal{C}}$
that is not contractible to a point. A simple choice is to take the curve
![]() $\unicode[STIX]{x1D701}=0$
. Then,
$\unicode[STIX]{x1D701}=0$
. Then,
As for the arc length
![]() $l$
,
$l$
,
where the integral on the right-hand side is taken at constant
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $l_{\text{max}}$
is determined by the intersection of the field line with
$l_{\text{max}}$
is determined by the intersection of the field line with
![]() ${\mathcal{C}}$
when it goes all the way around the torus.
${\mathcal{C}}$
when it goes all the way around the torus.
3 Dependence of
 $\unicode[STIX]{x1D711}^{(1)}$
on the collisionality and the radial electric field: a realistic numerical example
$\unicode[STIX]{x1D711}^{(1)}$
on the collisionality and the radial electric field: a realistic numerical example
Let us take realistic, stellarator reactor-relevant parameters,
![]() $\unicode[STIX]{x1D70C}_{\ast }=1.87\times 10^{-4}$
and
$\unicode[STIX]{x1D70C}_{\ast }=1.87\times 10^{-4}$
and
![]() $\unicode[STIX]{x1D716}=0.1$
, and let us employ the model magnetic field close to omnigeneity
$\unicode[STIX]{x1D716}=0.1$
, and let us employ the model magnetic field close to omnigeneity
![]() $B=B_{0}+\unicode[STIX]{x1D6FF}B_{1}$
described in § 2.5 (see (2.29), (2.48) and (2.49)). As for the profiles, we take
$B=B_{0}+\unicode[STIX]{x1D6FF}B_{1}$
described in § 2.5 (see (2.29), (2.48) and (2.49)). As for the profiles, we take
![]() $n^{\prime }/n=-(\unicode[STIX]{x1D716}R_{0})^{-1}$
and
$n^{\prime }/n=-(\unicode[STIX]{x1D716}R_{0})^{-1}$
and
![]() $T^{\prime }=0$
. We solve (2.18) and (2.25) with the code KNOSOS, and in figure 3 we represent the size of
$T^{\prime }=0$
. We solve (2.18) and (2.25) with the code KNOSOS, and in figure 3 we represent the size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
versus
$\unicode[STIX]{x1D711}^{(1)}$
versus
![]() $\unicode[STIX]{x1D708}_{\ast }$
. We plot curves corresponding to
$\unicode[STIX]{x1D708}_{\ast }$
. We plot curves corresponding to
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=0$
and to
$\unicode[STIX]{x1D711}_{0}^{\prime }=0$
and to
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=2\unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
. In this plot and in subsequent ones representing
$\unicode[STIX]{x1D711}_{0}^{\prime }=2\unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
. In this plot and in subsequent ones representing
![]() $\unicode[STIX]{x1D711}^{(1)}$
versus
$\unicode[STIX]{x1D711}^{(1)}$
versus
![]() $\unicode[STIX]{x1D708}_{\ast }$
, we typically take the maximum value of
$\unicode[STIX]{x1D708}_{\ast }$
, we typically take the maximum value of
![]() $\unicode[STIX]{x1D711}^{(1)}$
on the flux surface, and this is what we generally understand by ‘the size of
$\unicode[STIX]{x1D711}^{(1)}$
on the flux surface, and this is what we generally understand by ‘the size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
’. However, there are regimes (see § 4.3) in which the scaling of
$\unicode[STIX]{x1D711}^{(1)}$
’. However, there are regimes (see § 4.3) in which the scaling of
![]() $\unicode[STIX]{x1D711}^{(1)}$
at special points (lying in a very small spatial region associated with certain resonant trajectories) is different from that of
$\unicode[STIX]{x1D711}^{(1)}$
at special points (lying in a very small spatial region associated with certain resonant trajectories) is different from that of
![]() $\unicode[STIX]{x1D711}^{(1)}$
at generic points, far from the special points. When such regimes exist, we usually plot two curves and distinguish between ‘the size of
$\unicode[STIX]{x1D711}^{(1)}$
at generic points, far from the special points. When such regimes exist, we usually plot two curves and distinguish between ‘the size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
’ (see, for example, empty squares in figure 3), given by the maximum of
$\unicode[STIX]{x1D711}^{(1)}$
’ (see, for example, empty squares in figure 3), given by the maximum of
![]() $\unicode[STIX]{x1D711}^{(1)}$
on the flux surface, and ‘the size of
$\unicode[STIX]{x1D711}^{(1)}$
on the flux surface, and ‘the size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
at generic points’ (see, for example, full squares in figure 3). In order to compute the size of
$\unicode[STIX]{x1D711}^{(1)}$
at generic points’ (see, for example, full squares in figure 3). In order to compute the size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
at generic points, we take a spatial average of
$\unicode[STIX]{x1D711}^{(1)}$
at generic points, we take a spatial average of
![]() $\unicode[STIX]{x1D711}^{(1)}$
in a region where
$\unicode[STIX]{x1D711}^{(1)}$
in a region where
![]() $\unicode[STIX]{x1D711}^{(1)}$
is positive and which is far from the special points.
$\unicode[STIX]{x1D711}^{(1)}$
is positive and which is far from the special points.

Figure 3. Size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
as a function of the collisionality for a plasma with
$\unicode[STIX]{x1D711}^{(1)}$
as a function of the collisionality for a plasma with
![]() $\unicode[STIX]{x1D70C}_{\ast }=1.87\times 10^{-4}$
and magnetic configuration defined at the end of § 2.5 with
$\unicode[STIX]{x1D70C}_{\ast }=1.87\times 10^{-4}$
and magnetic configuration defined at the end of § 2.5 with
![]() $\unicode[STIX]{x1D716}=0.1$
. The circles correspond to results with
$\unicode[STIX]{x1D716}=0.1$
. The circles correspond to results with
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=2\unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
. The squares correspond to
$\unicode[STIX]{x1D711}_{0}^{\prime }=2\unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
. The squares correspond to
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=0$
. Empty squares give the size of
$\unicode[STIX]{x1D711}_{0}^{\prime }=0$
. Empty squares give the size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
. Full squares give the size of
$\unicode[STIX]{x1D711}^{(1)}$
. Full squares give the size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
at generic points (see the main text for the explanation on the difference between size of
$\unicode[STIX]{x1D711}^{(1)}$
at generic points (see the main text for the explanation on the difference between size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
and size of
$\unicode[STIX]{x1D711}^{(1)}$
and size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
at generic points). The important difference between the curves consisting of empty and full squares is that, for
$\unicode[STIX]{x1D711}^{(1)}$
at generic points). The important difference between the curves consisting of empty and full squares is that, for
![]() $\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }$
, the first one behaves as
$\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }$
, the first one behaves as
![]() $\unicode[STIX]{x1D708}_{\ast }^{-1/6}$
and the second one does not vary with
$\unicode[STIX]{x1D708}_{\ast }^{-1/6}$
and the second one does not vary with
![]() $\unicode[STIX]{x1D708}_{\ast }$
.
$\unicode[STIX]{x1D708}_{\ast }$
.
The dependence of
![]() $\unicode[STIX]{x1D711}^{(1)}$
on the collisionality and on the radial electric field shown in figure 3 is non-trivial. Understanding the different regimes encoded in a plot like figure 3 is the main subject of this paper. We will identify and study these regimes in § 4. As we will explain below, in order to have very clear numerical scalings in all the asymptotic regimes that (2.18) and (2.25) admit, in § 4 we will employ extremely small values of
$\unicode[STIX]{x1D711}^{(1)}$
on the collisionality and on the radial electric field shown in figure 3 is non-trivial. Understanding the different regimes encoded in a plot like figure 3 is the main subject of this paper. We will identify and study these regimes in § 4. As we will explain below, in order to have very clear numerical scalings in all the asymptotic regimes that (2.18) and (2.25) admit, in § 4 we will employ extremely small values of
![]() $\unicode[STIX]{x1D70C}_{\ast }$
and
$\unicode[STIX]{x1D70C}_{\ast }$
and
![]() $\unicode[STIX]{x1D716}$
in our numerical checks. The reader that prefers to skip the mathematical derivations of § 4 can go directly to table 1 in § 5 for a collection of the main analytical results.
$\unicode[STIX]{x1D716}$
in our numerical checks. The reader that prefers to skip the mathematical derivations of § 4 can go directly to table 1 in § 5 for a collection of the main analytical results.
4 Asymptotic regimes of
 $\unicode[STIX]{x1D711}^{(1)}$
at low collisionality
$\unicode[STIX]{x1D711}^{(1)}$
at low collisionality
In this section, we discuss the solution
![]() $\unicode[STIX]{x1D711}^{(1)}$
determined by equations (2.18) and (2.25) in three asymptotic low collisionality regimes. Namely, the
$\unicode[STIX]{x1D711}^{(1)}$
determined by equations (2.18) and (2.25) in three asymptotic low collisionality regimes. Namely, the
![]() $1/\unicode[STIX]{x1D708}$
regime, the
$1/\unicode[STIX]{x1D708}$
regime, the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime and the superbanana-plateau regime (the names of the regimes are due to the scaling of the radial neoclassical fluxes with collisionality, not necessarily to the scaling of
$\sqrt{\unicode[STIX]{x1D708}}$
regime and the superbanana-plateau regime (the names of the regimes are due to the scaling of the radial neoclassical fluxes with collisionality, not necessarily to the scaling of
![]() $\unicode[STIX]{x1D711}^{(1)}$
, as we will explain below). The subsection devoted to each regime will start with a discussion valid for arbitrary aspect ratio. Then, the results will be particularized for large aspect ratio stellarators and numerical examples of the most relevant analytical results will follow. In the course of the analytical derivations, it will become clear that, in order to clearly distinguish all the asymptotic regimes that equations (2.18) and (2.25) admit, the quantities
$\unicode[STIX]{x1D711}^{(1)}$
, as we will explain below). The subsection devoted to each regime will start with a discussion valid for arbitrary aspect ratio. Then, the results will be particularized for large aspect ratio stellarators and numerical examples of the most relevant analytical results will follow. In the course of the analytical derivations, it will become clear that, in order to clearly distinguish all the asymptotic regimes that equations (2.18) and (2.25) admit, the quantities
![]() $\unicode[STIX]{x1D70C}_{\ast }$
,
$\unicode[STIX]{x1D70C}_{\ast }$
,
![]() $\unicode[STIX]{x1D70C}_{\ast }/\unicode[STIX]{x1D716}^{1/2}$
and
$\unicode[STIX]{x1D70C}_{\ast }/\unicode[STIX]{x1D716}^{1/2}$
and
![]() $\unicode[STIX]{x1D70C}_{\ast }/\unicode[STIX]{x1D716}$
need to be sufficiently separated from each other. This is why, in what follows, we will take artificially small values for
$\unicode[STIX]{x1D70C}_{\ast }/\unicode[STIX]{x1D716}$
need to be sufficiently separated from each other. This is why, in what follows, we will take artificially small values for
![]() $\unicode[STIX]{x1D70C}_{\ast }$
and
$\unicode[STIX]{x1D70C}_{\ast }$
and
![]() $\unicode[STIX]{x1D716}$
, so that there is enough room between those quantities in our numerical examples. In these examples, we will always take
$\unicode[STIX]{x1D716}$
, so that there is enough room between those quantities in our numerical examples. In these examples, we will always take
![]() $\unicode[STIX]{x1D70C}_{\ast }=1.1\times 10^{-12}$
,
$\unicode[STIX]{x1D70C}_{\ast }=1.1\times 10^{-12}$
,
![]() $n^{\prime }/n=-(\unicode[STIX]{x1D716}R_{0})^{-1}$
and
$n^{\prime }/n=-(\unicode[STIX]{x1D716}R_{0})^{-1}$
and
![]() $T^{\prime }=0$
, and we will always employ the model magnetic field close to omnigeneity defined in § 2.5 (recall equations (2.29), (2.48) and (2.49)). We will use different values of
$T^{\prime }=0$
, and we will always employ the model magnetic field close to omnigeneity defined in § 2.5 (recall equations (2.29), (2.48) and (2.49)). We will use different values of
![]() $\unicode[STIX]{x1D716}$
and
$\unicode[STIX]{x1D716}$
and
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }$
that will be specified where appropriate.
$\unicode[STIX]{x1D711}_{0}^{\prime }$
that will be specified where appropriate.
4.1 The
 $1/\unicode[STIX]{x1D708}$
regime
$1/\unicode[STIX]{x1D708}$
regime
For tight aspect ratio stellarators, the
![]() $1/\unicode[STIX]{x1D708}$
regime corresponds to
$1/\unicode[STIX]{x1D708}$
regime corresponds to
![]() $\unicode[STIX]{x1D70C}_{\ast }\ll \unicode[STIX]{x1D708}_{\ast }\ll 1$
. In this situation, the first term on the left-hand side of (2.18) is negligible compared to the term on the right-hand side,
$\unicode[STIX]{x1D70C}_{\ast }\ll \unicode[STIX]{x1D708}_{\ast }\ll 1$
. In this situation, the first term on the left-hand side of (2.18) is negligible compared to the term on the right-hand side,
The correction to the Maxwellian distribution in the
![]() $1/\unicode[STIX]{x1D708}$
regime is therefore found by integrating the expression
$1/\unicode[STIX]{x1D708}$
regime is therefore found by integrating the expression
Below, we will find useful to distinguish between
![]() $g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{B}^{(1)}]$
and
$g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{B}^{(1)}]$
and
![]() $g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{\unicode[STIX]{x1D711}}^{(1)}]$
, where
$g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{\unicode[STIX]{x1D711}}^{(1)}]$
, where
and
and therefore
![]() $g_{1/\unicode[STIX]{x1D708}}^{(1)}=g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{B}^{(1)}]+g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{\unicode[STIX]{x1D711}}^{(1)}]$
. We note that
$g_{1/\unicode[STIX]{x1D708}}^{(1)}=g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{B}^{(1)}]+g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{\unicode[STIX]{x1D711}}^{(1)}]$
. We note that
and
The equation for
![]() $\unicode[STIX]{x1D711}^{(1)}$
reads (recall (2.25))
$\unicode[STIX]{x1D711}^{(1)}$
reads (recall (2.25))
Using (4.6) and
![]() $\unicode[STIX]{x1D70C}_{\ast }\ll \unicode[STIX]{x1D708}_{\ast }$
, and comparing the size of the left-hand side of (4.7) with the size of the term on the right-hand side containing
$\unicode[STIX]{x1D70C}_{\ast }\ll \unicode[STIX]{x1D708}_{\ast }$
, and comparing the size of the left-hand side of (4.7) with the size of the term on the right-hand side containing
![]() $g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{\unicode[STIX]{x1D711}}^{(1)}]$
, we conclude that the latter can be dropped. Hence,
$g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{\unicode[STIX]{x1D711}}^{(1)}]$
, we conclude that the latter can be dropped. Hence,
![]() $\unicode[STIX]{x1D711}^{(1)}$
is calculated as
$\unicode[STIX]{x1D711}^{(1)}$
is calculated as
Then, in the
![]() $1/\unicode[STIX]{x1D708}$
regime (see (4.5) and (4.6)),
$1/\unicode[STIX]{x1D708}$
regime (see (4.5) and (4.6)),
and
If
![]() $B_{0}$
and
$B_{0}$
and
![]() $B_{1}$
are stellarator symmetric,
$B_{1}$
are stellarator symmetric,
![]() $J_{B}^{(1)}$
is symmetric and, consequently,
$J_{B}^{(1)}$
is symmetric and, consequently,
![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}J_{B}^{(1)}$
is antisymmetric. Since the collision operator does not change the symmetry, the solution
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}J_{B}^{(1)}$
is antisymmetric. Since the collision operator does not change the symmetry, the solution
![]() $g_{1/\unicode[STIX]{x1D708}}^{(1)}$
of (4.2) is antisymmetric. Finally,
$g_{1/\unicode[STIX]{x1D708}}^{(1)}$
of (4.2) is antisymmetric. Finally,
![]() $\unicode[STIX]{x1D711}^{(1)}$
, obtained from (4.8), is stellarator antisymmetric.
$\unicode[STIX]{x1D711}^{(1)}$
, obtained from (4.8), is stellarator antisymmetric.
4.1.1 The
 $1/\unicode[STIX]{x1D708}$
regime in a large aspect ratio stellarator
$1/\unicode[STIX]{x1D708}$
regime in a large aspect ratio stellarator
As indicated by the end of § 2.4, when
![]() $\unicode[STIX]{x1D716}$
is small the low collisionality condition reads
$\unicode[STIX]{x1D716}$
is small the low collisionality condition reads
![]() $\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D716}^{3/2}$
. How small
$\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D716}^{3/2}$
. How small
![]() $\unicode[STIX]{x1D708}_{\ast }$
can be before the tangential drifts start to count depends on their size, as will be discussed mainly in §§ 4.2.1 and 4.2.2.
$\unicode[STIX]{x1D708}_{\ast }$
can be before the tangential drifts start to count depends on their size, as will be discussed mainly in §§ 4.2.1 and 4.2.2.
Let us refine the estimates (4.9) and (4.10) for the distribution function and the electrostatic potential when
![]() $\unicode[STIX]{x1D716}\ll 1$
. The drift-kinetic equation for
$\unicode[STIX]{x1D716}\ll 1$
. The drift-kinetic equation for
![]() $\unicode[STIX]{x1D716}\ll 1$
is
$\unicode[STIX]{x1D716}\ll 1$
is
Employing the scalings of § 2.4, it is easy to infer that
and
Next, we apply the
![]() $\unicode[STIX]{x1D716}\ll 1$
expansion to (4.7). We must treat two cases separately. If
$\unicode[STIX]{x1D716}\ll 1$
expansion to (4.7). We must treat two cases separately. If
then the first term on the right-hand side of (4.7) is negligible with respect to the left-hand side. Using that
![]() $\unicode[STIX]{x1D6E5}_{\text{trapped}}\sim \unicode[STIX]{x1D716}B_{00}^{-1}$
, we find
$\unicode[STIX]{x1D6E5}_{\text{trapped}}\sim \unicode[STIX]{x1D716}B_{00}^{-1}$
, we find
And noting that
![]() $g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{\unicode[STIX]{x1D711}}^{(1)}]\ll g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{B}^{(1)}]$
,
$g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{\unicode[STIX]{x1D711}}^{(1)}]\ll g_{1/\unicode[STIX]{x1D708}}^{(1)}[J_{B}^{(1)}]$
,
Then, both
![]() $\unicode[STIX]{x1D711}^{(1)}$
and
$\unicode[STIX]{x1D711}^{(1)}$
and
![]() $g^{(1)}$
scale as
$g^{(1)}$
scale as
![]() $\unicode[STIX]{x1D708}_{\ast }^{-1}$
. The fact that
$\unicode[STIX]{x1D708}_{\ast }^{-1}$
. The fact that
![]() $\unicode[STIX]{x1D711}^{(1)}$
is antisymmetric is also clear. In figure 4, a contour plot of
$\unicode[STIX]{x1D711}^{(1)}$
is antisymmetric is also clear. In figure 4, a contour plot of
![]() $\unicode[STIX]{x1D711}^{(1)}$
on the magnetic surface is provided for a set of values such that (4.14) holds.
$\unicode[STIX]{x1D711}^{(1)}$
on the magnetic surface is provided for a set of values such that (4.14) holds.

Figure 4. Contour plot of
![]() $\unicode[STIX]{x1D711}^{(1)}$
for
$\unicode[STIX]{x1D711}^{(1)}$
for
![]() $\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
,
$\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
,
![]() $\unicode[STIX]{x1D708}_{\ast }=10^{-7}$
and
$\unicode[STIX]{x1D708}_{\ast }=10^{-7}$
and
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=0$
.
$\unicode[STIX]{x1D711}_{0}^{\prime }=0$
.
However, if
![]() $\unicode[STIX]{x1D708}_{\ast }\sim \unicode[STIX]{x1D716}^{-1/2}\unicode[STIX]{x1D70C}_{\ast }$
or smaller, the first term on the right-hand side of (4.7) can become comparable to the left-hand side. Let us study the asymptotic regime
$\unicode[STIX]{x1D708}_{\ast }\sim \unicode[STIX]{x1D716}^{-1/2}\unicode[STIX]{x1D70C}_{\ast }$
or smaller, the first term on the right-hand side of (4.7) can become comparable to the left-hand side. Let us study the asymptotic regime
From (4.7) we learn that
![]() $\unicode[STIX]{x1D711}^{(1)}$
depends on
$\unicode[STIX]{x1D711}^{(1)}$
depends on
![]() $l$
only through
$l$
only through
![]() $B_{0}$
. This will be important in a moment. When (4.17) holds, the left-hand side of (4.7) is small compared to the term on the right-hand side that involves
$B_{0}$
. This will be important in a moment. When (4.17) holds, the left-hand side of (4.7) is small compared to the term on the right-hand side that involves
![]() $\unicode[STIX]{x1D711}^{(1)}$
. Then, we can write
$\unicode[STIX]{x1D711}^{(1)}$
. Then, we can write
where
![]() $g_{1/\unicode[STIX]{x1D708}}^{(1)}$
is the solution of (4.11). For the argument that follows, we find it convenient to write
$g_{1/\unicode[STIX]{x1D708}}^{(1)}$
is the solution of (4.11). For the argument that follows, we find it convenient to write
![]() $J^{(1)}$
as
$J^{(1)}$
as
Here,
![]() $B_{0,\text{min}}$
is the minimum of
$B_{0,\text{min}}$
is the minimum of
![]() $B_{0}$
,
$B_{0}$
,
and we have used the magnitude of
![]() $B_{0}$
as the integration variable in (4.19). Since there are two valuesFootnote
8
of
$B_{0}$
as the integration variable in (4.19). Since there are two valuesFootnote
8
of
![]() $l$
corresponding to each value
$l$
corresponding to each value
![]() $B_{0}=\hat{B}$
, we introduce the discrete coordinate
$B_{0}=\hat{B}$
, we introduce the discrete coordinate
![]() $\unicode[STIX]{x1D6FD}=\pm 1$
. The value
$\unicode[STIX]{x1D6FD}=\pm 1$
. The value
![]() $\unicode[STIX]{x1D6FD}=-1$
labels the branch of the magnetic well where
$\unicode[STIX]{x1D6FD}=-1$
labels the branch of the magnetic well where
![]() $\unicode[STIX]{x2202}_{l}B_{0}<0$
and the value
$\unicode[STIX]{x2202}_{l}B_{0}<0$
and the value
![]() $\unicode[STIX]{x1D6FD}=1$
labels the branch where
$\unicode[STIX]{x1D6FD}=1$
labels the branch where
![]() $\unicode[STIX]{x2202}_{l}B_{0}\geqslant 0$
. On the right-hand side of (4.20), every function is understood to be expressed using
$\unicode[STIX]{x2202}_{l}B_{0}\geqslant 0$
. On the right-hand side of (4.20), every function is understood to be expressed using
![]() $\hat{B}$
and
$\hat{B}$
and
![]() $\unicode[STIX]{x1D6FD}$
instead of
$\unicode[STIX]{x1D6FD}$
instead of
![]() $l$
. In particular, we note that, in general,
$l$
. In particular, we note that, in general,
![]() $|\unicode[STIX]{x2202}_{l}B_{0}|(\hat{B},\unicode[STIX]{x1D6FD})\neq |\unicode[STIX]{x2202}_{l}B_{0}|(\hat{B},-\unicode[STIX]{x1D6FD})$
.
$|\unicode[STIX]{x2202}_{l}B_{0}|(\hat{B},\unicode[STIX]{x1D6FD})\neq |\unicode[STIX]{x2202}_{l}B_{0}|(\hat{B},-\unicode[STIX]{x1D6FD})$
.
It is clear that
gives the solution of (4.18) and that, by imposing (4.21), we obtain a relation between the orbit integrals of
![]() $B_{1}$
and
$B_{1}$
and
![]() $\unicode[STIX]{x1D711}^{(1)}$
. The orbit integral of a function can be interpreted as a transformation that replaces the coordinate
$\unicode[STIX]{x1D711}^{(1)}$
. The orbit integral of a function can be interpreted as a transformation that replaces the coordinate
![]() $l$
by the coordinate
$l$
by the coordinate
![]() $\unicode[STIX]{x1D706}$
. This can be viewed as an Abel transform, and an explicit inversion formula is given in appendix A. In principle, the inversion cannot distinguish between two points of the magnetic well with the same value of
$\unicode[STIX]{x1D706}$
. This can be viewed as an Abel transform, and an explicit inversion formula is given in appendix A. In principle, the inversion cannot distinguish between two points of the magnetic well with the same value of
![]() $B_{0}$
(this is quite intuitive when we use the magnitude of
$B_{0}$
(this is quite intuitive when we use the magnitude of
![]() $B_{0}$
as the integration variable, as we have done in (4.19)). Carrying out the integral in
$B_{0}$
as the integration variable, as we have done in (4.19)). Carrying out the integral in
![]() $v$
on the left-hand side of (4.21), we arrive at
$v$
on the left-hand side of (4.21), we arrive at
Recalling that
![]() $\unicode[STIX]{x1D711}^{(1)}$
depends on
$\unicode[STIX]{x1D711}^{(1)}$
depends on
![]() $l$
only through
$l$
only through
![]() $B_{0}$
(see (4.7)), we finally obtain the explicit solution
$B_{0}$
(see (4.7)), we finally obtain the explicit solution
From (4.23) we infer that in this regime
![]() $\unicode[STIX]{x1D711}^{(1)}$
is stellarator symmetric and that its size, in general, is
$\unicode[STIX]{x1D711}^{(1)}$
is stellarator symmetric and that its size, in general, is
We note that for particular combinations of the profile gradients,
![]() $\unicode[STIX]{x1D711}^{(1)}$
can get larger because the denominator of (4.23) can become small. This will be studied elsewhere.
$\unicode[STIX]{x1D711}^{(1)}$
can get larger because the denominator of (4.23) can become small. This will be studied elsewhere.
In figure 5, a contour plot of
![]() $\unicode[STIX]{x1D711}^{(1)}$
on the magnetic surface is provided for a set of values that satisfy (4.17).
$\unicode[STIX]{x1D711}^{(1)}$
on the magnetic surface is provided for a set of values that satisfy (4.17).
Finally, we have (see (4.12) and (4.13))
In figure 6, and for
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=0$
, we illustrate the scaling of
$\unicode[STIX]{x1D711}_{0}^{\prime }=0$
, we illustrate the scaling of
![]() $\unicode[STIX]{x1D711}^{(1)}$
and of
$\unicode[STIX]{x1D711}^{(1)}$
and of
in a range of collisionality values such that both regimes, (4.14) and (4.17), are observed. Whereas
![]() $\unicode[STIX]{x1D711}^{(1)}$
and
$\unicode[STIX]{x1D711}^{(1)}$
and
![]() $n_{B}$
have the same scaling with
$n_{B}$
have the same scaling with
![]() $\unicode[STIX]{x1D708}_{\ast }$
in the regime (4.14), they scale differently in the regime (4.17).
$\unicode[STIX]{x1D708}_{\ast }$
in the regime (4.14), they scale differently in the regime (4.17).

Figure 5. Contour plot of
![]() $\unicode[STIX]{x1D711}^{(1)}$
for
$\unicode[STIX]{x1D711}^{(1)}$
for
![]() $\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
,
$\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
,
![]() $\unicode[STIX]{x1D708}_{\ast }=5.8\times 10^{-11}$
and
$\unicode[STIX]{x1D708}_{\ast }=5.8\times 10^{-11}$
and
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=0$
.
$\unicode[STIX]{x1D711}_{0}^{\prime }=0$
.

Figure 6. Scaling of
![]() $\unicode[STIX]{x1D711}^{(1)}$
and
$\unicode[STIX]{x1D711}^{(1)}$
and
![]() $n_{B}$
(evaluated at the point of the flux surface where they reach their maximum values) with
$n_{B}$
(evaluated at the point of the flux surface where they reach their maximum values) with
![]() $\unicode[STIX]{x1D708}_{\ast }$
and
$\unicode[STIX]{x1D708}_{\ast }$
and
![]() $\unicode[STIX]{x1D716}$
. Here,
$\unicode[STIX]{x1D716}$
. Here,
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=0$
. The regimes (4.14) and (4.17) are confirmed numerically. The central value
$\unicode[STIX]{x1D711}_{0}^{\prime }=0$
. The regimes (4.14) and (4.17) are confirmed numerically. The central value
![]() $\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
has been used to draw the thin dotted lines indicating where the collisionality values
$\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
has been used to draw the thin dotted lines indicating where the collisionality values
![]() $\unicode[STIX]{x1D70C}_{\ast }/\unicode[STIX]{x1D716}^{1/2}$
and
$\unicode[STIX]{x1D70C}_{\ast }/\unicode[STIX]{x1D716}^{1/2}$
and
![]() $\unicode[STIX]{x1D716}^{3/2}$
are located.
$\unicode[STIX]{x1D716}^{3/2}$
are located.
4.2 The
 $\sqrt{\unicode[STIX]{x1D708}}$
regime
$\sqrt{\unicode[STIX]{x1D708}}$
regime
We turn to discuss collisionality regimes with
![]() $\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }\ll 1$
. In this situation, as explained at length in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), the behaviour of both the radial neoclassical fluxes and
$\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }\ll 1$
. In this situation, as explained at length in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), the behaviour of both the radial neoclassical fluxes and
![]() $\unicode[STIX]{x1D711}^{(1)}$
depends on the zeroes of
$\unicode[STIX]{x1D711}^{(1)}$
depends on the zeroes of
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}$
.
$\unicode[STIX]{x2202}_{r}J^{(0)}$
.
When
![]() $\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }$
, the collision term in (2.18) is negligible compared to the first term on the left-hand side,
$\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }$
, the collision term in (2.18) is negligible compared to the first term on the left-hand side,
Hence, to lowest order in an expansion in
![]() $\unicode[STIX]{x1D708}_{\ast }/\unicode[STIX]{x1D70C}_{\ast }$
,
$\unicode[STIX]{x1D708}_{\ast }/\unicode[STIX]{x1D70C}_{\ast }$
,
where
![]() $g_{0}$
is the solution of
$g_{0}$
is the solution of
This equation can be readily solved, obtaining an explicit expression for
![]() $g_{0}$
,
$g_{0}$
,
where we have chosen
![]() $\int _{0}^{2\unicode[STIX]{x03C0}}g_{0}\text{d}\unicode[STIX]{x1D6FC}=0$
to fix the integration constant. From (4.30), it is clear that the solution
$\int _{0}^{2\unicode[STIX]{x03C0}}g_{0}\text{d}\unicode[STIX]{x1D6FC}=0$
to fix the integration constant. From (4.30), it is clear that the solution
![]() $g_{0}$
is not valid at phase space points where
$g_{0}$
is not valid at phase space points where
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}$
vanishes, and we devote § 4.3 to those points. However, if
$\unicode[STIX]{x2202}_{r}J^{(0)}$
vanishes, and we devote § 4.3 to those points. However, if
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}$
does not vanish at any point of phase space (or if it vanishes only for values of the velocity
$\unicode[STIX]{x2202}_{r}J^{(0)}$
does not vanish at any point of phase space (or if it vanishes only for values of the velocity
![]() $v\gg v_{t}$
, that are irrelevant because their effect is supressed by the smallness of the Maxwellian distribution), (4.30) is enough to correctly determine
$v\gg v_{t}$
, that are irrelevant because their effect is supressed by the smallness of the Maxwellian distribution), (4.30) is enough to correctly determine
![]() $\unicode[STIX]{x1D711}^{(1)}$
via the quasineutrality equation
$\unicode[STIX]{x1D711}^{(1)}$
via the quasineutrality equation
In this case,
![]() $\unicode[STIX]{x1D711}^{(1)}$
is stellarator symmetric (due to the fact that the expression (4.30) for
$\unicode[STIX]{x1D711}^{(1)}$
is stellarator symmetric (due to the fact that the expression (4.30) for
![]() $g_{0}$
does not involve derivatives of
$g_{0}$
does not involve derivatives of
![]() $B$
along the flux surface) and does not scale with collisionality,
$B$
along the flux surface) and does not scale with collisionality,
As proven in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017),
![]() $g_{0}$
does not contribute to the radial neoclassical fluxes. They are determined by corrections to
$g_{0}$
does not contribute to the radial neoclassical fluxes. They are determined by corrections to
![]() $g_{0}$
in (4.28) that are localized in a region of phase space that has a typical size
$g_{0}$
in (4.28) that are localized in a region of phase space that has a typical size
![]() $\unicode[STIX]{x1D6E5}_{\sqrt{\unicode[STIX]{x1D708}}}\sim \sqrt{\unicode[STIX]{x1D708}_{\ast }/\unicode[STIX]{x1D70C}_{\ast }}$
in the coordinate
$\unicode[STIX]{x1D6E5}_{\sqrt{\unicode[STIX]{x1D708}}}\sim \sqrt{\unicode[STIX]{x1D708}_{\ast }/\unicode[STIX]{x1D70C}_{\ast }}$
in the coordinate
![]() $\unicode[STIX]{x1D706}$
. This small layer produces the scaling with collisionality that justifies the name of this regime, the
$\unicode[STIX]{x1D706}$
. This small layer produces the scaling with collisionality that justifies the name of this regime, the
![]() $\sqrt{\unicode[STIX]{x1D708}}$
regime.
$\sqrt{\unicode[STIX]{x1D708}}$
regime.
If the aspect ratio is large, it is interesting to distinguish two cases (mostly in connection to the solutions of the quasineutrality equation), to which we devote §§ 4.2.1 and 4.2.2.
4.2.1 Large aspect ratio and large tangential drift,
 $\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-3/2}v_{t}R_{0}$
$\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-3/2}v_{t}R_{0}$
If
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-3/2}v_{t}R_{0}$
, the inequality (4.27) holds provided that
$\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-3/2}v_{t}R_{0}$
, the inequality (4.27) holds provided that
![]() $\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D70C}_{\ast }$
. Hence, the
$\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D70C}_{\ast }$
. Hence, the
![]() $1/\unicode[STIX]{x1D708}$
regime takes place in the range
$1/\unicode[STIX]{x1D708}$
regime takes place in the range
In particular, the regime defined by (4.17) is not observed because the tangential drift starts to count for collisionalities much larger than
![]() $\unicode[STIX]{x1D716}^{-1/2}\unicode[STIX]{x1D70C}_{\ast }$
. It can be observed, however, when the tangential drift is smaller (see § 4.2.2).
$\unicode[STIX]{x1D716}^{-1/2}\unicode[STIX]{x1D70C}_{\ast }$
. It can be observed, however, when the tangential drift is smaller (see § 4.2.2).
As pointed out in § 2.4,
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-3/2}v_{t}R_{0}$
corresponds to
$\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-3/2}v_{t}R_{0}$
corresponds to
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }\sim \unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
, which is the standard size of the radial electric field in a large aspect ratio stellarator. The derivation of the radial fluxes in this regime can be found, for example, in Galeev & Sagdeev (Reference Galeev, Sagdeev and Leontovich1979), Ho & Kulsrud (Reference Ho and Kulsrud1987).
$\unicode[STIX]{x1D711}_{0}^{\prime }\sim \unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
, which is the standard size of the radial electric field in a large aspect ratio stellarator. The derivation of the radial fluxes in this regime can be found, for example, in Galeev & Sagdeev (Reference Galeev, Sagdeev and Leontovich1979), Ho & Kulsrud (Reference Ho and Kulsrud1987).
Let us start the discussion about
![]() $\unicode[STIX]{x1D711}^{(1)}$
by writing (4.31) more explicitly. Inserting in (4.31) the expression for
$\unicode[STIX]{x1D711}^{(1)}$
by writing (4.31) more explicitly. Inserting in (4.31) the expression for
![]() $g_{0}$
(see (4.30)) and rearranging, we get
$g_{0}$
(see (4.30)) and rearranging, we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D711}^{(1)}-\frac{2\unicode[STIX]{x03C0}}{en}\left(\frac{Z}{T}+\frac{1}{T_{e}}\right)^{-1}\int _{0}^{\infty }\text{d}v\int _{B_{0,\text{max}}^{-1}}^{B_{0}^{-1}}\text{d}\unicode[STIX]{x1D706}\frac{v^{3}B_{0}}{|v_{\Vert }^{(0)}|}\frac{\unicode[STIX]{x1D6F6}F_{M}}{\unicode[STIX]{x2202}_{r}J^{(0)}}\widetilde{J}_{\unicode[STIX]{x1D711}}^{(1)}\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{2\unicode[STIX]{x03C0}}{en}\left(\frac{Z}{T}+\frac{1}{T_{e}}\right)^{-1}\int _{0}^{\infty }\text{d}v\int _{B_{0,\text{max}}^{-1}}^{B_{0}^{-1}}\text{d}\unicode[STIX]{x1D706}\frac{v^{3}B_{0}}{|v_{\Vert }^{(0)}|}\frac{\unicode[STIX]{x1D6F6}F_{M}}{\unicode[STIX]{x2202}_{r}J^{(0)}}\widetilde{J}_{B}^{(1)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D711}^{(1)}-\frac{2\unicode[STIX]{x03C0}}{en}\left(\frac{Z}{T}+\frac{1}{T_{e}}\right)^{-1}\int _{0}^{\infty }\text{d}v\int _{B_{0,\text{max}}^{-1}}^{B_{0}^{-1}}\text{d}\unicode[STIX]{x1D706}\frac{v^{3}B_{0}}{|v_{\Vert }^{(0)}|}\frac{\unicode[STIX]{x1D6F6}F_{M}}{\unicode[STIX]{x2202}_{r}J^{(0)}}\widetilde{J}_{\unicode[STIX]{x1D711}}^{(1)}\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{2\unicode[STIX]{x03C0}}{en}\left(\frac{Z}{T}+\frac{1}{T_{e}}\right)^{-1}\int _{0}^{\infty }\text{d}v\int _{B_{0,\text{max}}^{-1}}^{B_{0}^{-1}}\text{d}\unicode[STIX]{x1D706}\frac{v^{3}B_{0}}{|v_{\Vert }^{(0)}|}\frac{\unicode[STIX]{x1D6F6}F_{M}}{\unicode[STIX]{x2202}_{r}J^{(0)}}\widetilde{J}_{B}^{(1)},\end{eqnarray}$$
where
and
In (4.36) we have emphasized that only the component of
![]() $J_{\unicode[STIX]{x1D711}}^{(1)}$
that fluctuates in
$J_{\unicode[STIX]{x1D711}}^{(1)}$
that fluctuates in
![]() $\unicode[STIX]{x1D6FC}$
enters (4.34) although, strictly speaking, it is superfluous due to (2.27).
$\unicode[STIX]{x1D6FC}$
enters (4.34) although, strictly speaking, it is superfluous due to (2.27).
Recalling the estimates in § 2.4, it is straightforward to see that the second term on the left-hand side of (4.34) is smaller than the first one by a factor
![]() $\unicode[STIX]{x1D716}^{1/2}$
. Hence, the size of
$\unicode[STIX]{x1D716}^{1/2}$
. Hence, the size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
is determined by the size of the right-hand side of (4.34). That is,
$\unicode[STIX]{x1D711}^{(1)}$
is determined by the size of the right-hand side of (4.34). That is,
This scaling is consistent with (4.15) when
![]() $\unicode[STIX]{x1D708}_{\ast }\sim \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D70C}_{\ast }$
. In figure 7, a contour plot of
$\unicode[STIX]{x1D708}_{\ast }\sim \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D70C}_{\ast }$
. In figure 7, a contour plot of
![]() $\unicode[STIX]{x1D711}^{(1)}$
corresponding to
$\unicode[STIX]{x1D711}^{(1)}$
corresponding to
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-3/2}v_{t}R_{0}$
and
$\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-3/2}v_{t}R_{0}$
and
![]() $\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D70C}_{\ast }$
is shown. In figure 8, the collisionality-independent scaling (4.37) for
$\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D70C}_{\ast }$
is shown. In figure 8, the collisionality-independent scaling (4.37) for
![]() $\unicode[STIX]{x1D711}^{(1)}$
is numerically checked.
$\unicode[STIX]{x1D711}^{(1)}$
is numerically checked.

Figure 7. Contour plot of
![]() $\unicode[STIX]{x1D711}^{(1)}$
for
$\unicode[STIX]{x1D711}^{(1)}$
for
![]() $\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
,
$\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
,
![]() $\unicode[STIX]{x1D708}_{\ast }=1.1\times 10^{-10}$
and
$\unicode[STIX]{x1D708}_{\ast }=1.1\times 10^{-10}$
and
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=2\unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
.
$\unicode[STIX]{x1D711}_{0}^{\prime }=2\unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
.

Figure 8. Scaling of
![]() $\unicode[STIX]{x1D711}^{(1)}$
with
$\unicode[STIX]{x1D711}^{(1)}$
with
![]() $\unicode[STIX]{x1D708}_{\ast }$
and
$\unicode[STIX]{x1D708}_{\ast }$
and
![]() $\unicode[STIX]{x1D716}$
(evaluated at the point of the flux surface where it reaches its maximum value) in a range of values of the collisionality where (4.37) is observed. Here,
$\unicode[STIX]{x1D716}$
(evaluated at the point of the flux surface where it reaches its maximum value) in a range of values of the collisionality where (4.37) is observed. Here,
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=2\unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
.
$\unicode[STIX]{x1D711}_{0}^{\prime }=2\unicode[STIX]{x1D716}^{-1}T/(eR_{0})$
.
4.2.2 Large aspect ratio and small tangential drift,
 $\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-1/2}v_{t}R_{0}$
$\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-1/2}v_{t}R_{0}$
If
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-1/2}v_{t}R_{0}$
, (4.27) is satisfied when
$\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-1/2}v_{t}R_{0}$
, (4.27) is satisfied when
![]() $\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }$
. Therefore, for such typical size of the tangential drifts, the
$\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }$
. Therefore, for such typical size of the tangential drifts, the
![]() $1/\unicode[STIX]{x1D708}$
regime happens for collisionality values
$1/\unicode[STIX]{x1D708}$
regime happens for collisionality values
To be precise, in the range
![]() $\unicode[STIX]{x1D70C}_{\ast }\ll \unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D716}^{-1/2}\unicode[STIX]{x1D70C}_{\ast }$
, the subregime (4.17) of the
$\unicode[STIX]{x1D70C}_{\ast }\ll \unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D716}^{-1/2}\unicode[STIX]{x1D70C}_{\ast }$
, the subregime (4.17) of the
![]() $1/\unicode[STIX]{x1D708}$
regime will be observed.
$1/\unicode[STIX]{x1D708}$
regime will be observed.
When
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-1/2}v_{t}R_{0}$
, the left-hand side of (4.31) can be neglected compared to the term on the right-hand side containing
$\unicode[STIX]{x2202}_{r}J^{(0)}\sim \unicode[STIX]{x1D716}^{-1/2}v_{t}R_{0}$
, the left-hand side of (4.31) can be neglected compared to the term on the right-hand side containing
![]() $\unicode[STIX]{x1D711}^{(1)}$
, so that we have
$\unicode[STIX]{x1D711}^{(1)}$
, so that we have
which can be solved by finding the solution of
One could formally proceed as done after equation (4.17), but it seems difficult to find a completely explicit solution for
![]() $\unicode[STIX]{x1D711}^{(1)}$
due to the relatively complicated dependence of
$\unicode[STIX]{x1D711}^{(1)}$
due to the relatively complicated dependence of
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}$
on
$\unicode[STIX]{x2202}_{r}J^{(0)}$
on
![]() $v$
and
$v$
and
![]() $\unicode[STIX]{x1D706}$
. In any case, it is clear that imposing (4.40) implies
$\unicode[STIX]{x1D706}$
. In any case, it is clear that imposing (4.40) implies
and, therefore,
In addition, from (4.40) we can infer that
![]() $\unicode[STIX]{x1D711}^{(1)}$
is stellarator symmetric.
$\unicode[STIX]{x1D711}^{(1)}$
is stellarator symmetric.
Note that for
![]() $\unicode[STIX]{x1D708}_{\ast }\sim \unicode[STIX]{x1D70C}_{\ast }$
, expression (4.42) matches (4.24).
$\unicode[STIX]{x1D708}_{\ast }\sim \unicode[STIX]{x1D70C}_{\ast }$
, expression (4.42) matches (4.24).
4.3 Superbanana-plateau regime
In this subsection, we treat cases with
![]() $\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }\ll 1$
and such that
$\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }\ll 1$
and such that
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}$
vanishes for
$\unicode[STIX]{x2202}_{r}J^{(0)}$
vanishes for
![]() $v\lesssim v_{t}$
. Sections 4.1 and 4.2, although brief, were self-contained to a large extent. In this subsection we will refer the reader to Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) more frequently for the derivation of particularly technical results.
$v\lesssim v_{t}$
. Sections 4.1 and 4.2, although brief, were self-contained to a large extent. In this subsection we will refer the reader to Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) more frequently for the derivation of particularly technical results.
The zeroes of
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}$
correspond to ‘resonant’ points of phase space where the orbit-averaged tangential component of the magnetic and
$\unicode[STIX]{x2202}_{r}J^{(0)}$
correspond to ‘resonant’ points of phase space where the orbit-averaged tangential component of the magnetic and
![]() $E\times B$
drifts cancel each other.
$E\times B$
drifts cancel each other.
Recall equation (2.19). The condition
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}=0$
can be compactly expressed as
$\unicode[STIX]{x2202}_{r}J^{(0)}=0$
can be compactly expressed as
where
denotes orbit average and
is the time that it takes for the particle to complete the orbit in the magnetic field
![]() $B_{0}$
. A necessary (but not sufficient) condition for this equation to have solutions for
$B_{0}$
. A necessary (but not sufficient) condition for this equation to have solutions for
![]() $v\lesssim v_{t}$
is
$v\lesssim v_{t}$
is
That is, the effect of the resonances is expected to be important for relatively small values of the radial electric field. When
![]() $\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }\ll 1$
and
$\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }\ll 1$
and
![]() $Ze|\unicode[STIX]{x1D711}_{0}^{\prime }|/T\gg R_{0}^{-1}$
, the treatment of subsection (4.2) applies.
$Ze|\unicode[STIX]{x1D711}_{0}^{\prime }|/T\gg R_{0}^{-1}$
, the treatment of subsection (4.2) applies.
From here on, let us assume
![]() $\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }\ll 1$
and condition (4.46) in the rest of this subsection, and let us also assume that, for
$\unicode[STIX]{x1D708}_{\ast }\ll \unicode[STIX]{x1D70C}_{\ast }\ll 1$
and condition (4.46) in the rest of this subsection, and let us also assume that, for
![]() $v\lesssim v_{t}$
, there exists one solution in
$v\lesssim v_{t}$
, there exists one solution in
![]() $\unicode[STIX]{x1D706}$
of the resonance condition (4.43), that we denote by
$\unicode[STIX]{x1D706}$
of the resonance condition (4.43), that we denote by
![]() $\unicode[STIX]{x1D706}_{r}(r,v,\unicode[STIX]{x1D711}_{0}^{\prime })$
. In general,
$\unicode[STIX]{x1D706}_{r}(r,v,\unicode[STIX]{x1D711}_{0}^{\prime })$
. In general,
![]() $\unicode[STIX]{x1D706}_{r}$
will be defined only for some values of
$\unicode[STIX]{x1D706}_{r}$
will be defined only for some values of
![]() $r$
,
$r$
,
![]() $v$
and
$v$
and
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }$
. For fixed
$\unicode[STIX]{x1D711}_{0}^{\prime }$
. For fixed
![]() $r$
and
$r$
and
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }$
, we denote by
$\unicode[STIX]{x1D711}_{0}^{\prime }$
, we denote by
![]() $I$
the interval in
$I$
the interval in
![]() $v$
for which
$v$
for which
![]() $\unicode[STIX]{x1D706}_{r}$
is defined.
$\unicode[STIX]{x1D706}_{r}$
is defined.
We can expand the drift-kinetic equation (2.18) around the position of the resonance. Defining
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{r}(r,v,\unicode[STIX]{x1D711}_{0}^{\prime })$
and writing the drift-kinetic equation in coordinates
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{r}(r,v,\unicode[STIX]{x1D711}_{0}^{\prime })$
and writing the drift-kinetic equation in coordinates
![]() $v$
and
$v$
and
![]() $\unicode[STIX]{x1D709}$
, we have
$\unicode[STIX]{x1D709}$
, we have
where
![]() $k(r,v)$
is given by
$k(r,v)$
is given by
subindices
![]() $r$
indicate that the corresponding quantity is evaluated at
$r$
indicate that the corresponding quantity is evaluated at
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{r}(r,v,\unicode[STIX]{x1D711}_{0}^{\prime })$
and
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{r}(r,v,\unicode[STIX]{x1D711}_{0}^{\prime })$
and
![]() $\widehat{J_{\unicode[STIX]{x1D711}}^{(1)}}$
is an approximation of
$\widehat{J_{\unicode[STIX]{x1D711}}^{(1)}}$
is an approximation of
![]() $J_{\unicode[STIX]{x1D711}}^{(1)}$
around
$J_{\unicode[STIX]{x1D711}}^{(1)}$
around
![]() $\unicode[STIX]{x1D706}_{r}$
. In particular,
$\unicode[STIX]{x1D706}_{r}$
. In particular,
![]() $\widehat{J_{\unicode[STIX]{x1D711}}^{(1)}}$
is a function of
$\widehat{J_{\unicode[STIX]{x1D711}}^{(1)}}$
is a function of
![]() $v$
and
$v$
and
![]() $\unicode[STIX]{x1D709}$
. We will see shortly why, in general, we cannot simply evaluate
$\unicode[STIX]{x1D709}$
. We will see shortly why, in general, we cannot simply evaluate
![]() $J_{\unicode[STIX]{x1D711}}^{(1)}$
at
$J_{\unicode[STIX]{x1D711}}^{(1)}$
at
![]() $\unicode[STIX]{x1D706}_{r}$
. The second term in (4.48) comes from the energy diffusion piece of the collision operator, which must be included because the coordinate across the layer (the coordinate in which
$\unicode[STIX]{x1D706}_{r}$
. The second term in (4.48) comes from the energy diffusion piece of the collision operator, which must be included because the coordinate across the layer (the coordinate in which
![]() $g_{\text{rl}}$
varies fast),
$g_{\text{rl}}$
varies fast),
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{r}$
, mixes
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{r}$
, mixes
![]() $v$
and
$v$
and
![]() $\unicode[STIX]{x1D706}$
. The collision frequency
$\unicode[STIX]{x1D706}$
. The collision frequency
![]() $\unicode[STIX]{x1D708}_{v}$
is given by
$\unicode[STIX]{x1D708}_{v}$
is given by
In Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), the energy diffusion piece of the collision operator was incorrectly neglected. Note that none of the scalings derived in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) are affected by the inclusion of energy diffusion.
Using that
![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x2202}_{r}J_{r}^{(0)}=O(B_{0}v_{t})$
and that
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x2202}_{r}J_{r}^{(0)}=O(B_{0}v_{t})$
and that
![]() $k(r,v)=O(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}B_{0}^{-2}R_{0}\unicode[STIX]{x1D70C}_{\ast }^{-1})$
, and balancing the two terms on the left-hand side of (4.47), we deduce that
$k(r,v)=O(\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}B_{0}^{-2}R_{0}\unicode[STIX]{x1D70C}_{\ast }^{-1})$
, and balancing the two terms on the left-hand side of (4.47), we deduce that
![]() $g_{\text{rl}}$
is localized in a layer whose size in the coordinate
$g_{\text{rl}}$
is localized in a layer whose size in the coordinate
![]() $\unicode[STIX]{x1D709}$
is
$\unicode[STIX]{x1D709}$
is
Then, balancing the left- and right-hand sides of (4.47), we find that
This resonant layer, via
![]() $g_{\text{rl}}$
, is responsible for superbanana-plateau transport.
$g_{\text{rl}}$
, is responsible for superbanana-plateau transport.
The solution outside the resonant layer is given by (4.30). Since
![]() $g_{0}$
diverges at
$g_{0}$
diverges at
![]() $\unicode[STIX]{x1D706}_{r}$
, we remove the divergence so that we obtain a function
$\unicode[STIX]{x1D706}_{r}$
, we remove the divergence so that we obtain a function
![]() $g_{0}^{\text{out}}$
which is finite everywhere and asymptotically coincides with
$g_{0}^{\text{out}}$
which is finite everywhere and asymptotically coincides with
![]() $g_{0}$
far from the resonant layer. Namely,
$g_{0}$
far from the resonant layer. Namely,
where
![]() $\widetilde{J}_{B,r}^{(1)}$
is the quantity defined in (4.35) evaluated at
$\widetilde{J}_{B,r}^{(1)}$
is the quantity defined in (4.35) evaluated at
![]() $\unicode[STIX]{x1D706}_{r}$
.
$\unicode[STIX]{x1D706}_{r}$
.
In principle, both pieces,
![]() $g_{0}^{\text{out}}$
and
$g_{0}^{\text{out}}$
and
![]() $g_{\text{rl}}$
, contribute equally to the quasineutrality equation (although only
$g_{\text{rl}}$
, contribute equally to the quasineutrality equation (although only
![]() $g_{\text{rl}}$
contributes to radial transport). Hence, one needs to solve
$g_{\text{rl}}$
contributes to radial transport). Hence, one needs to solve
with
![]() $K\gg 1$
. An explicit, asymptotically correct expression for the quasineutrality equation is given by (see Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) for the details)
$K\gg 1$
. An explicit, asymptotically correct expression for the quasineutrality equation is given by (see Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) for the details)
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}^{(1)} & = & \displaystyle \frac{2\unicode[STIX]{x03C0}B_{0}}{en}\left(\frac{Z}{T}+\frac{1}{T_{e}}\right)^{-1}\left\{\int _{0}^{\infty }\text{d}v\int _{B_{0,\text{max}}^{-1}}^{B^{-1}}\text{d}\unicode[STIX]{x1D706}\frac{v^{3}}{|v_{\Vert }^{(0)}|}g_{0}^{\text{out}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\int _{I}\text{d}v\,v^{2}\int _{-\infty }^{\unicode[STIX]{x1D706}_{L}(l)}\text{d}\unicode[STIX]{x1D706}\frac{g_{\text{rl}}}{\sqrt{\unicode[STIX]{x1D706}_{r}|\unicode[STIX]{x2202}_{l}B_{0}(l_{L})|(l-l_{L})-(\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{r})B_{0}(l_{L})}}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{I}\text{d}v\,v^{2}\int _{-\infty }^{\unicode[STIX]{x1D706}_{R}(l)}\text{d}\unicode[STIX]{x1D706}\frac{g_{\text{rl}}}{\sqrt{\unicode[STIX]{x1D706}_{r}|\unicode[STIX]{x2202}_{l}B_{0}(l_{R})|(l_{R}-l)-(\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{r})B_{0}(l_{R})}}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{I}\text{d}v\,v^{2}\left[\frac{1}{\sqrt{1-\unicode[STIX]{x1D706}_{r}B_{0}(l)}}-\frac{1}{\sqrt{\unicode[STIX]{x1D706}_{r}|\unicode[STIX]{x2202}_{l}B_{0}(l_{L})|(l-l_{L})}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\left.\frac{1}{\sqrt{\unicode[STIX]{x1D706}_{r}|\unicode[STIX]{x2202}_{l}B_{0}(l_{R})|(l_{R}-l)}}\right]\int _{-\infty }^{\infty }\text{d}\unicode[STIX]{x1D706}\,g_{\text{rl}}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}^{(1)} & = & \displaystyle \frac{2\unicode[STIX]{x03C0}B_{0}}{en}\left(\frac{Z}{T}+\frac{1}{T_{e}}\right)^{-1}\left\{\int _{0}^{\infty }\text{d}v\int _{B_{0,\text{max}}^{-1}}^{B^{-1}}\text{d}\unicode[STIX]{x1D706}\frac{v^{3}}{|v_{\Vert }^{(0)}|}g_{0}^{\text{out}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\int _{I}\text{d}v\,v^{2}\int _{-\infty }^{\unicode[STIX]{x1D706}_{L}(l)}\text{d}\unicode[STIX]{x1D706}\frac{g_{\text{rl}}}{\sqrt{\unicode[STIX]{x1D706}_{r}|\unicode[STIX]{x2202}_{l}B_{0}(l_{L})|(l-l_{L})-(\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{r})B_{0}(l_{L})}}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{I}\text{d}v\,v^{2}\int _{-\infty }^{\unicode[STIX]{x1D706}_{R}(l)}\text{d}\unicode[STIX]{x1D706}\frac{g_{\text{rl}}}{\sqrt{\unicode[STIX]{x1D706}_{r}|\unicode[STIX]{x2202}_{l}B_{0}(l_{R})|(l_{R}-l)-(\unicode[STIX]{x1D706}-\unicode[STIX]{x1D706}_{r})B_{0}(l_{R})}}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{I}\text{d}v\,v^{2}\left[\frac{1}{\sqrt{1-\unicode[STIX]{x1D706}_{r}B_{0}(l)}}-\frac{1}{\sqrt{\unicode[STIX]{x1D706}_{r}|\unicode[STIX]{x2202}_{l}B_{0}(l_{L})|(l-l_{L})}}\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\left.\frac{1}{\sqrt{\unicode[STIX]{x1D706}_{r}|\unicode[STIX]{x2202}_{l}B_{0}(l_{R})|(l_{R}-l)}}\right]\int _{-\infty }^{\infty }\text{d}\unicode[STIX]{x1D706}\,g_{\text{rl}}\right\},\end{eqnarray}$$
where
![]() $l_{L}$
and
$l_{L}$
and
![]() $l_{R}$
denote the bounce points of the trajectory
$l_{R}$
denote the bounce points of the trajectory
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{r}$
,
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{r}$
,
and
Expression (4.54) is useful in order to explain why we did not evaluate
![]() $J_{\unicode[STIX]{x1D711}}^{(1)}$
at
$J_{\unicode[STIX]{x1D711}}^{(1)}$
at
![]() $\unicode[STIX]{x1D706}_{r}$
in (4.47). First, note that the first term in brackets in the fourth line of (4.54) diverges at
$\unicode[STIX]{x1D706}_{r}$
in (4.47). First, note that the first term in brackets in the fourth line of (4.54) diverges at
![]() $l=l_{L}$
and
$l=l_{L}$
and
![]() $l=l_{R}$
. We distinguish two cases:
$l=l_{R}$
. We distinguish two cases:
(i) If
(4.57)the dependence of $$\begin{eqnarray}\left|\frac{2Ze\unicode[STIX]{x1D711}_{0}^{\prime }}{mv^{2}\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D706}}\overline{\unicode[STIX]{x2202}_{r}B_{0}}(\unicode[STIX]{x1D706}_{r})}\right|\gg \unicode[STIX]{x1D6E5}_{\text{sb-p}},\end{eqnarray}$$
$$\begin{eqnarray}\left|\frac{2Ze\unicode[STIX]{x1D711}_{0}^{\prime }}{mv^{2}\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D706}}\overline{\unicode[STIX]{x2202}_{r}B_{0}}(\unicode[STIX]{x1D706}_{r})}\right|\gg \unicode[STIX]{x1D6E5}_{\text{sb-p}},\end{eqnarray}$$
 $\unicode[STIX]{x1D706}_{r}$
on
$\unicode[STIX]{x1D706}_{r}$
on
 $v$
is strong enough for the integral over
$v$
is strong enough for the integral over
 $v$
to smooth out the divergence of
$v$
to smooth out the divergence of
 $1/\sqrt{1-\unicode[STIX]{x1D706}_{r}B_{0}(l)}$
at
$1/\sqrt{1-\unicode[STIX]{x1D706}_{r}B_{0}(l)}$
at
 $l=l_{L}$
and
$l=l_{L}$
and
 $l=l_{R}$
. Then, (4.58)In this case,
$l=l_{R}$
. Then, (4.58)In this case, $$\begin{eqnarray}\unicode[STIX]{x1D711}^{(1)}\sim \frac{T}{e}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}^{(1)}\sim \frac{T}{e}.\end{eqnarray}$$
 $\widehat{J_{\unicode[STIX]{x1D711}}^{(1)}}$
can be replaced by
$\widehat{J_{\unicode[STIX]{x1D711}}^{(1)}}$
can be replaced by
 $J_{\unicode[STIX]{x1D711},r}^{(1)}$
in (4.47), where (4.59)
$J_{\unicode[STIX]{x1D711},r}^{(1)}$
in (4.47), where (4.59) $$\begin{eqnarray}J_{\unicode[STIX]{x1D711},r}^{(1)}=-\frac{2Ze}{mv}\int _{l_{b_{10}}}^{l_{b_{20}}}\frac{\unicode[STIX]{x1D711}^{(1)}}{\sqrt{1-\unicode[STIX]{x1D706}_{r}B_{0}}}\,\text{d}l,\end{eqnarray}$$
$$\begin{eqnarray}J_{\unicode[STIX]{x1D711},r}^{(1)}=-\frac{2Ze}{mv}\int _{l_{b_{10}}}^{l_{b_{20}}}\frac{\unicode[STIX]{x1D711}^{(1)}}{\sqrt{1-\unicode[STIX]{x1D706}_{r}B_{0}}}\,\text{d}l,\end{eqnarray}$$

Figure 9. If (4.60) is satisfied, the resonant value
 $\unicode[STIX]{x1D706}_{r}$
is approximately independent of
$\unicode[STIX]{x1D706}_{r}$
is approximately independent of
 $v$
. The accumulated effect of the resonance for all possible values of
$v$
. The accumulated effect of the resonance for all possible values of
 $v$
produces a larger
$v$
produces a larger
 $\unicode[STIX]{x1D711}^{(1)}$
in a neighbourhood of the bounce points of the resonant trajectory,
$\unicode[STIX]{x1D711}^{(1)}$
in a neighbourhood of the bounce points of the resonant trajectory,
 $l_{L}$
and
$l_{L}$
and
 $l_{R}$
.
$l_{R}$
.and the solution of (4.47) can be found analytically, with
 $g_{\text{rl}}$
approaching a Dirac delta distribution when the collision frequency tends to zero. This gives the standard superbanana-plateau regime in which the radial neoclassical fluxes are strictly independent of the collisionality. This regime was treated in Shaing (Reference Shaing2015) for tokamaks of finite aspect ratio with broken symmetry.
$g_{\text{rl}}$
approaching a Dirac delta distribution when the collision frequency tends to zero. This gives the standard superbanana-plateau regime in which the radial neoclassical fluxes are strictly independent of the collisionality. This regime was treated in Shaing (Reference Shaing2015) for tokamaks of finite aspect ratio with broken symmetry.(ii) If
(4.60)then $$\begin{eqnarray}\left|\frac{2Ze\unicode[STIX]{x1D711}_{0}^{\prime }}{mv^{2}\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D706}}\overline{\unicode[STIX]{x2202}_{r}B_{0}}(\unicode[STIX]{x1D706}_{r})}\right|\ll \unicode[STIX]{x1D6E5}_{\text{sb-p}},\end{eqnarray}$$
$$\begin{eqnarray}\left|\frac{2Ze\unicode[STIX]{x1D711}_{0}^{\prime }}{mv^{2}\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D706}}\overline{\unicode[STIX]{x2202}_{r}B_{0}}(\unicode[STIX]{x1D706}_{r})}\right|\ll \unicode[STIX]{x1D6E5}_{\text{sb-p}},\end{eqnarray}$$
 $\unicode[STIX]{x1D706}_{r}$
is approximately independent of
$\unicode[STIX]{x1D706}_{r}$
is approximately independent of
 $v$
and no such smoothing happens. The effect of the accumulation of the resonances at the same
$v$
and no such smoothing happens. The effect of the accumulation of the resonances at the same
 $\unicode[STIX]{x1D706}_{r}$
for every
$\unicode[STIX]{x1D706}_{r}$
for every
 $v$
means that, close to the bounce points of the resonant trajectory, the electrostatic potential becomes very large. Specifically, one finds that (4.61)where
$v$
means that, close to the bounce points of the resonant trajectory, the electrostatic potential becomes very large. Specifically, one finds that (4.61)where $$\begin{eqnarray}\unicode[STIX]{x1D711}^{(1)}\sim \left\{\begin{array}{@{}ll@{}}(\unicode[STIX]{x1D708}_{\ast }/\unicode[STIX]{x1D70C}_{\ast })^{-1/6}T/e\quad & |l-l_{j}|\sim B_{0}\unicode[STIX]{x1D6E5}_{\text{sb-p}}R_{0}\\ T/e\quad & |l-l_{j}|\gg B_{0}\unicode[STIX]{x1D6E5}_{\text{sb-p}}R_{0},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}^{(1)}\sim \left\{\begin{array}{@{}ll@{}}(\unicode[STIX]{x1D708}_{\ast }/\unicode[STIX]{x1D70C}_{\ast })^{-1/6}T/e\quad & |l-l_{j}|\sim B_{0}\unicode[STIX]{x1D6E5}_{\text{sb-p}}R_{0}\\ T/e\quad & |l-l_{j}|\gg B_{0}\unicode[STIX]{x1D6E5}_{\text{sb-p}}R_{0},\end{array}\right.\end{eqnarray}$$
 $j=L,R$
(see figure 9). This subregime of the superbanana-plateau regime was discovered in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) and we will focus on it in the next subsection, devoted to illustrating it numerically. When (4.60) holds, the radial neoclassical fluxes depend logarithmically on collisionality. The estimation (4.50) for the size of the layer also incorporates logarithmic corrections.
$j=L,R$
(see figure 9). This subregime of the superbanana-plateau regime was discovered in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) and we will focus on it in the next subsection, devoted to illustrating it numerically. When (4.60) holds, the radial neoclassical fluxes depend logarithmically on collisionality. The estimation (4.50) for the size of the layer also incorporates logarithmic corrections.

Figure 10. Plot of
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}$
as a function of
$\unicode[STIX]{x2202}_{r}J^{(0)}$
as a function of
![]() $\unicode[STIX]{x1D706}$
in our model omnigenous magnetic field, with
$\unicode[STIX]{x1D706}$
in our model omnigenous magnetic field, with
![]() $\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
and
$\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
and
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=0$
. The value of
$\unicode[STIX]{x1D711}_{0}^{\prime }=0$
. The value of
![]() $\unicode[STIX]{x1D706}$
at which
$\unicode[STIX]{x1D706}$
at which
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}$
vanishes determines the resonant value
$\unicode[STIX]{x2202}_{r}J^{(0)}$
vanishes determines the resonant value
![]() $\unicode[STIX]{x1D706}_{r}$
. Here,
$\unicode[STIX]{x1D706}_{r}$
. Here,
![]() $(B_{0,\text{max}}\unicode[STIX]{x1D706}_{r}-1)/(B_{0,\text{max}}/B_{0,\text{min}}-1)=0.04$
.
$(B_{0,\text{max}}\unicode[STIX]{x1D706}_{r}-1)/(B_{0,\text{max}}/B_{0,\text{min}}-1)=0.04$
.
Figure 11. Contour plot of
![]() $\unicode[STIX]{x1D711}^{(1)}$
for
$\unicode[STIX]{x1D711}^{(1)}$
for
![]() $\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
,
$\unicode[STIX]{x1D716}=1.1\times 10^{-4}$
,
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=0$
and three values of the collisionality. From left to right,
$\unicode[STIX]{x1D711}_{0}^{\prime }=0$
and three values of the collisionality. From left to right,
![]() $\unicode[STIX]{x1D708}_{\ast }=1.2\times 10^{-12}$
,
$\unicode[STIX]{x1D708}_{\ast }=1.2\times 10^{-12}$
,
![]() $\unicode[STIX]{x1D708}_{\ast }=1.3\times 10^{-13}$
,
$\unicode[STIX]{x1D708}_{\ast }=1.3\times 10^{-13}$
,
![]() $\unicode[STIX]{x1D708}_{\ast }=1.3\times 10^{-14}$
. The black lines are the two curves determined by the left and right bounce points of the resonant trajectory,
$\unicode[STIX]{x1D708}_{\ast }=1.3\times 10^{-14}$
. The black lines are the two curves determined by the left and right bounce points of the resonant trajectory,
![]() $l_{L}$
and
$l_{L}$
and
![]() $l_{R}$
, respectively. When
$l_{R}$
, respectively. When
![]() $\unicode[STIX]{x1D708}_{\ast }$
decreases, the increase of
$\unicode[STIX]{x1D708}_{\ast }$
decreases, the increase of
![]() $\unicode[STIX]{x1D711}^{(1)}$
around
$\unicode[STIX]{x1D711}^{(1)}$
around
![]() $l_{L}$
and
$l_{L}$
and
![]() $l_{R}$
, as predicted by (4.67), is confirmed. The colour scale has been kept constant in the three panels, so that the increase in
$l_{R}$
, as predicted by (4.67), is confirmed. The colour scale has been kept constant in the three panels, so that the increase in
![]() $\unicode[STIX]{x1D711}^{(1)}$
becomes clearer; that is, in (b,c),
$\unicode[STIX]{x1D711}^{(1)}$
becomes clearer; that is, in (b,c),
![]() $e|\unicode[STIX]{x1D711}^{(1)}|/(T\unicode[STIX]{x1D716})$
reaches larger values than the largest one indicated in the colour scale bar.
$e|\unicode[STIX]{x1D711}^{(1)}|/(T\unicode[STIX]{x1D716})$
reaches larger values than the largest one indicated in the colour scale bar.

Figure 12. Size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
as a function of
$\unicode[STIX]{x1D711}^{(1)}$
as a function of
![]() $\unicode[STIX]{x1D708}_{\ast }$
and
$\unicode[STIX]{x1D708}_{\ast }$
and
![]() $\unicode[STIX]{x1D716}$
. Here,
$\unicode[STIX]{x1D716}$
. Here,
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=0$
. The two scalings given in (4.67) are checked. Full squares give the size of
$\unicode[STIX]{x1D711}_{0}^{\prime }=0$
. The two scalings given in (4.67) are checked. Full squares give the size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
at generic points,
$\unicode[STIX]{x1D711}^{(1)}$
at generic points,
![]() $|l-l_{j}|\gg B_{00}\unicode[STIX]{x1D6E5}_{\text{sb-p}}R_{0}$
, whereas empty squares give the size of
$|l-l_{j}|\gg B_{00}\unicode[STIX]{x1D6E5}_{\text{sb-p}}R_{0}$
, whereas empty squares give the size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
at a point that is very close to a bounce point of the resonant trajectory,
$\unicode[STIX]{x1D711}^{(1)}$
at a point that is very close to a bounce point of the resonant trajectory,
![]() $|l-l_{j}|\sim B_{00}\unicode[STIX]{x1D6E5}_{\text{sb-p}}R_{0}$
(that is, empty squares give approximately the maximum of
$|l-l_{j}|\sim B_{00}\unicode[STIX]{x1D6E5}_{\text{sb-p}}R_{0}$
(that is, empty squares give approximately the maximum of
![]() $\unicode[STIX]{x1D711}^{(1)}$
on the flux surface).
$\unicode[STIX]{x1D711}^{(1)}$
on the flux surface).
Finally, we point out that, as clearly inferred from inspection of (4.47),
![]() $g_{\text{rl}}$
has no definite parity under stellarator symmetry transformations, and neither does
$g_{\text{rl}}$
has no definite parity under stellarator symmetry transformations, and neither does
![]() $\unicode[STIX]{x1D711}^{(1)}$
.
$\unicode[STIX]{x1D711}^{(1)}$
.
4.3.1 Superbanana-plateau regime in a large aspect ratio stellarator
We start by giving some estimates that are needed below. First, note that
![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x2202}_{r}J_{r}^{(0)}\sim \unicode[STIX]{x1D716}^{-3/2}v_{t}B_{00}$
. Second, observe that for large aspect ratio
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x2202}_{r}J_{r}^{(0)}\sim \unicode[STIX]{x1D716}^{-3/2}v_{t}B_{00}$
. Second, observe that for large aspect ratio
![]() $\unicode[STIX]{x2202}_{v}\unicode[STIX]{x1D706}_{r}\sim \unicode[STIX]{x1D716}/(B_{00}v_{t})$
so that the term proportional to
$\unicode[STIX]{x2202}_{v}\unicode[STIX]{x1D706}_{r}\sim \unicode[STIX]{x1D716}/(B_{00}v_{t})$
so that the term proportional to
![]() $\unicode[STIX]{x1D708}_{v}$
in (4.48) can be neglected compared to the term proportional to
$\unicode[STIX]{x1D708}_{v}$
in (4.48) can be neglected compared to the term proportional to
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}$
, giving
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}$
, giving
![]() $k\sim \unicode[STIX]{x1D716}^{3/2}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}B_{00}^{-2}R_{0}\unicode[STIX]{x1D70C}_{\ast }^{-1}$
. Then, balancing the two terms on the left-hand side of the drift-kinetic equation (4.47), we find that, for
$k\sim \unicode[STIX]{x1D716}^{3/2}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D706}}B_{00}^{-2}R_{0}\unicode[STIX]{x1D70C}_{\ast }^{-1}$
. Then, balancing the two terms on the left-hand side of the drift-kinetic equation (4.47), we find that, for
![]() $\unicode[STIX]{x1D716}\ll 1$
,
$\unicode[STIX]{x1D716}\ll 1$
,
For convenience, define
![]() $g_{\text{rl}}[J_{B}^{(1)}]$
and
$g_{\text{rl}}[J_{B}^{(1)}]$
and
![]() $g_{\text{rl}}[J_{\unicode[STIX]{x1D711}}^{(1)}]$
as the solutions of
$g_{\text{rl}}[J_{\unicode[STIX]{x1D711}}^{(1)}]$
as the solutions of
and
respectively. Of course,
![]() $g_{\text{rl}}=g_{\text{rl}}[J_{B}^{(1)}]+g_{\text{rl}}[J_{\unicode[STIX]{x1D711}}^{(1)}]$
. Then,
$g_{\text{rl}}=g_{\text{rl}}[J_{B}^{(1)}]+g_{\text{rl}}[J_{\unicode[STIX]{x1D711}}^{(1)}]$
. Then,
and
One can deal with the quasineutrality equation (4.54) by employing again the procedure followed after (4.17) and also in § 4.2.2. The result is that
Let us check numerically the scalings of this subsection. First, in figure 10, we show the dependence of
![]() $\unicode[STIX]{x2202}_{r}J^{(0)}$
on
$\unicode[STIX]{x2202}_{r}J^{(0)}$
on
![]() $\unicode[STIX]{x1D706}$
for
$\unicode[STIX]{x1D706}$
for
![]() $\unicode[STIX]{x1D711}_{0}^{\prime }=0$
in our model magnetic configuration and we give, in particular, the location in phase space of the resonant value
$\unicode[STIX]{x1D711}_{0}^{\prime }=0$
in our model magnetic configuration and we give, in particular, the location in phase space of the resonant value
![]() $\unicode[STIX]{x1D706}_{r}$
. In figure 11, contour plots of
$\unicode[STIX]{x1D706}_{r}$
. In figure 11, contour plots of
![]() $\unicode[STIX]{x1D711}^{(1)}$
are shown for three different values of the collisionality, so that one can see how
$\unicode[STIX]{x1D711}^{(1)}$
are shown for three different values of the collisionality, so that one can see how
![]() $\unicode[STIX]{x1D711}^{(1)}$
becomes larger and larger around
$\unicode[STIX]{x1D711}^{(1)}$
becomes larger and larger around
![]() $l_{L}$
and
$l_{L}$
and
![]() $l_{R}$
as the collisionality decreases. Figure 12 provides a precise numerical check of the two scalings given in (4.67).
$l_{R}$
as the collisionality decreases. Figure 12 provides a precise numerical check of the two scalings given in (4.67).
5 Conclusions
The component of the neoclassical electrostatic potential that is non-constant on flux surfaces,
![]() $\tilde{\unicode[STIX]{x1D711}}$
(equivalently, the component of the electric field that is tangential to the surface), has been proven to have an important impact on stellarator radial impurity transport (García-Regaña et al.
Reference García-Regaña, Kleiber, Beidler, Turkin, Maassberg and Helander2013), triggering interest in the correct calculation of the tangential electric field, which has often been neglected in stellarator neoclassical theory. On the numerical side, remarkable effort has been made during recent years (see García-Regaña et al. (Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017) and references therein). In this article, we have studied analytically the scaling of
$\tilde{\unicode[STIX]{x1D711}}$
(equivalently, the component of the electric field that is tangential to the surface), has been proven to have an important impact on stellarator radial impurity transport (García-Regaña et al.
Reference García-Regaña, Kleiber, Beidler, Turkin, Maassberg and Helander2013), triggering interest in the correct calculation of the tangential electric field, which has often been neglected in stellarator neoclassical theory. On the numerical side, remarkable effort has been made during recent years (see García-Regaña et al. (Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017) and references therein). In this article, we have studied analytically the scaling of
![]() $\tilde{\unicode[STIX]{x1D711}}$
with collisionality and aspect ratio, and its structure on the flux surface.
$\tilde{\unicode[STIX]{x1D711}}$
with collisionality and aspect ratio, and its structure on the flux surface.
The tangential electric field can be remarkably large when the collisionality is low enough for the tangential drifts to count in the drift-kinetic equation and especially when the tangential magnetic drift is non-negligible. If the collisionality and the radial electric field are such that the tangential magnetic drift cannot be dropped, the neoclassical equations can be kept linear and radially local only if the stellarator is sufficiently optimized (Calvo et al.
Reference Calvo, Parra, Velasco and Alonso2017); i.e. if the magnetic configuration is sufficiently close to omnigeneity (Cary & Shasharina Reference Cary and Shasharina1997; Parra et al.
Reference Parra, Calvo, Helander and Landreman2015). This is why we have conducted our study in the framework of a stellarator that is close to being omnigenous, employing the techniques developed in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), where a small parameter
![]() $\unicode[STIX]{x1D6FF}$
exists that gives the size of the deviation from perfect omnigeneity. Throughout the paper, and employing some results of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), we discuss the calculation of the tangential electric field for collisionality values that cover the
$\unicode[STIX]{x1D6FF}$
exists that gives the size of the deviation from perfect omnigeneity. Throughout the paper, and employing some results of Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017), we discuss the calculation of the tangential electric field for collisionality values that cover the
![]() $1/\unicode[STIX]{x1D708}$
,
$1/\unicode[STIX]{x1D708}$
,
![]() $\sqrt{\unicode[STIX]{x1D708}}$
and superbanana-plateau regimes, and in each of them provide its size, scaling with collisionality, aspect ratio and
$\sqrt{\unicode[STIX]{x1D708}}$
and superbanana-plateau regimes, and in each of them provide its size, scaling with collisionality, aspect ratio and
![]() $\unicode[STIX]{x1D6FF}$
and behaviour under stellarator symmetry transformations. In the treatment presented in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) no assumption was made about the aspect ratio of the stellarator. Here, we have investigated how the results are modified when, apart from the
$\unicode[STIX]{x1D6FF}$
and behaviour under stellarator symmetry transformations. In the treatment presented in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) no assumption was made about the aspect ratio of the stellarator. Here, we have investigated how the results are modified when, apart from the
![]() $\unicode[STIX]{x1D6FF}$
expansion, one takes a subsidiary expansion in large aspect ratio. We have found new regimes that did not appear in tight aspect ratio devices. In particular, we have deduced that the maximum size admitted for
$\unicode[STIX]{x1D6FF}$
expansion, one takes a subsidiary expansion in large aspect ratio. We have found new regimes that did not appear in tight aspect ratio devices. In particular, we have deduced that the maximum size admitted for
![]() $\tilde{\unicode[STIX]{x1D711}}:=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{(1)}$
by the neoclassical equations is given by
$\tilde{\unicode[STIX]{x1D711}}:=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{(1)}$
by the neoclassical equations is given by
![]() $\unicode[STIX]{x1D711}^{(1)}\sim \unicode[STIX]{x1D716}T/e$
, except at some special points where it can be larger. Table 1 summarizes the analytical results, providing the scaling with collisionality and aspect ratio in each regime. The notation is explained in §§ 2 and 4.
$\unicode[STIX]{x1D711}^{(1)}\sim \unicode[STIX]{x1D716}T/e$
, except at some special points where it can be larger. Table 1 summarizes the analytical results, providing the scaling with collisionality and aspect ratio in each regime. The notation is explained in §§ 2 and 4.
The analytical results for each asymptotic regime have been verified and illustrated by numerical calculations of the code KNOSOS, that solves the equations derived in Calvo et al. (Reference Calvo, Parra, Velasco and Alonso2017) for stellarators close to omnigeneity, the same set of equations that are the subject of study of this paper. In figure 3, choosing realistic values for a stellarator reactor plasma, we have represented the size of
![]() $\unicode[STIX]{x1D711}^{(1)}$
as a function of the collisionality, showing the different regimes in a single figure.
$\unicode[STIX]{x1D711}^{(1)}$
as a function of the collisionality, showing the different regimes in a single figure.
Finally, we comment on the expected effect of
![]() $\tilde{\unicode[STIX]{x1D711}}$
on the radial neoclassical transport of the main ions. This effect is negligible compared to the transport due to
$\tilde{\unicode[STIX]{x1D711}}$
on the radial neoclassical transport of the main ions. This effect is negligible compared to the transport due to
![]() $B_{1}$
except in regimes where
$B_{1}$
except in regimes where
![]() $\tilde{\unicode[STIX]{x1D711}}$
reaches its maximum size, given by
$\tilde{\unicode[STIX]{x1D711}}$
reaches its maximum size, given by
![]() $\unicode[STIX]{x1D711}^{(1)}\sim \unicode[STIX]{x1D716}T/e$
(see table 1). In principle, in such regimes, the contributions of
$\unicode[STIX]{x1D711}^{(1)}\sim \unicode[STIX]{x1D716}T/e$
(see table 1). In principle, in such regimes, the contributions of
![]() $B_{1}$
and
$B_{1}$
and
![]() $\tilde{\unicode[STIX]{x1D711}}$
to the main ion neoclassical fluxes can be comparable. In practice, however, the maximum size reached by
$\tilde{\unicode[STIX]{x1D711}}$
to the main ion neoclassical fluxes can be comparable. In practice, however, the maximum size reached by
![]() $\tilde{\unicode[STIX]{x1D711}}$
is somewhat smaller. Obtaining
$\tilde{\unicode[STIX]{x1D711}}$
is somewhat smaller. Obtaining
![]() $\unicode[STIX]{x1D711}^{(1)}\sim \unicode[STIX]{x1D716}T/e$
seems to require density profile gradients
$\unicode[STIX]{x1D711}^{(1)}\sim \unicode[STIX]{x1D716}T/e$
seems to require density profile gradients
![]() $|n^{\prime }/n|\sim (\unicode[STIX]{x1D716}R_{0})^{-1}$
, like the ones employed in this paper. If one takes a smaller density profile gradient and
$|n^{\prime }/n|\sim (\unicode[STIX]{x1D716}R_{0})^{-1}$
, like the ones employed in this paper. If one takes a smaller density profile gradient and
![]() $|T^{\prime }/T|\sim (\unicode[STIX]{x1D716}R_{0})^{-1}$
(a situation that is more common in stellarators), the scaling of
$|T^{\prime }/T|\sim (\unicode[STIX]{x1D716}R_{0})^{-1}$
(a situation that is more common in stellarators), the scaling of
![]() $\tilde{\unicode[STIX]{x1D711}}$
does not change but the actual value is smaller, due to the different way in which the density and temperature profiles enter the source term of the drift-kinetic equation.
$\tilde{\unicode[STIX]{x1D711}}$
does not change but the actual value is smaller, due to the different way in which the density and temperature profiles enter the source term of the drift-kinetic equation.
Table 1. Asymptotic regimes for
![]() $\unicode[STIX]{x1D711}^{(1)}$
.
$\unicode[STIX]{x1D711}^{(1)}$
.

Acknowledgements
The authors would like to thank an anonymous referee for pointing out that, in general, the energy diffusion piece of the collision operator cannot be neglected in (4.47). This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 under grant agreement no. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. This research was supported in part by grant ENE2015-70142-P, Ministerio de Economía y Competitividad, Spain.
Appendix A. Application of the Abel transform to integrals over trapped trajectories
We give a useful inversion formula that interchanges the coordinates
![]() $l$
and
$l$
and
![]() $\unicode[STIX]{x1D706}$
. In this appendix, the coordinates
$\unicode[STIX]{x1D706}$
. In this appendix, the coordinates
![]() $r$
,
$r$
,
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $v$
are irrelevant, and we omit them.
$v$
are irrelevant, and we omit them.
For any function
![]() $f(l)$
, we define
$f(l)$
, we define
![]() $F(\unicode[STIX]{x1D706})$
as the following integral over the trapped trajectory determined by
$F(\unicode[STIX]{x1D706})$
as the following integral over the trapped trajectory determined by
![]() $\unicode[STIX]{x1D706}\in [B_{0,\text{max}}^{-1},B_{0,\text{min}}^{-1}]$
,
$\unicode[STIX]{x1D706}\in [B_{0,\text{max}}^{-1},B_{0,\text{min}}^{-1}]$
,
Then, given a value of the magnetic field
![]() $\hat{B}\in [B_{0,\text{min}},B_{0,\text{max}}]$
, we have
$\hat{B}\in [B_{0,\text{min}},B_{0,\text{max}}]$
, we have
which can be proven by direct check. This formula can be viewed as a particularization of the Abel transform (Abel Reference Abel1826).
For the sake of the application of the inversion formula in the main text of this article, we point out the following property, which is immediately derived from (A 2): if
![]() $f(l)$
is such that
$f(l)$
is such that
![]() $B_{0}(l_{1})=B_{0}(l_{2})\Rightarrow f(l_{1})=f(l_{2})$
, then
$B_{0}(l_{1})=B_{0}(l_{2})\Rightarrow f(l_{1})=f(l_{2})$
, then