Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T08:22:55.611Z Has data issue: false hasContentIssue false
  • English
  • Français

A fully implicit numerical integration of the relativistic particle equation of motion

Part of: PLA The Vlasov Equation

Published online by Cambridge University Press:  24 April 2017

J. Pétri
J. Pétri*
Affiliation:
Université de Strasbourg, CNRS, Observatoire astronomique de Strasbourg, UMR 7550, F-67000 Strasbourg, France
*
†Email address for correspondence: jerome.petri@astro.unistra.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Relativistic strongly magnetized plasmas are produced in laboratories thanks to state-of-the-art laser technology but can naturally be found around compact objects such as neutron stars and black holes. Detailed studies of the behaviour of relativistic plasmas require accurate computations able to catch the full spatial and temporal dynamics of the system. Numerical simulations of ultra-relativistic plasmas face severe restrictions due to limitations in the maximum possible Lorentz factors that current algorithms can reproduce to good accuracy. In order to circumvent this flaw and repel the limit to 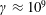$\unicode[STIX]{x1D6FE}\approx 10^{9}$, we design a new fully implicit scheme to solve the relativistic particle equation of motion in an external electromagnetic field using a three-dimensional Cartesian geometry. We show some examples of numerical integrations in constant electromagnetic fields to prove the efficiency of our algorithm. The code is also able to follow the electric drift motion for high Lorentz factors. In the most general case of spatially and temporally varying electromagnetic fields, the code performs extremely well, as shown by comparison with exact analytical solutions for the relativistic electrostatic Kepler problem as well as for linearly and circularly polarized plane waves.

Keywords

astrophysical plasmasmagnetized plasmasplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 2 , April 2017 , 705830206
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Birdsall, C. K. & Langdon, A. B. 2005 Plasma Physics Via Computer Simulation. IOP Publishing.Google Scholar
Boris, J. P. 1970 Relativistic plasma simulation-optimization of a hybrid code. In Proceedings of the Fourth Conference on Numerical Simulations of Plasmas held at the Naval Research Laboratory, Washington DC, 1970.Google Scholar
He, Y., Sun, Y., Zhang, R., Wang, Y., Liu, J. & Qin, H. 2016 High order volume-preserving algorithms for relativistic charged particles in general electromagnetic fields. Phys. Plasmas 23 (9), 092109.Google Scholar
Higuera, A. V. & Cary, J. R.2017 Structure-preserving second-order integration of relativistic charged particle trajectories in electromagnetic fields. arXiv:1701.05605 [physics].Google Scholar
Hockney, R. W. & Eastwood, J. W. 1988 Computer Simulation Using Particles. CRC Press & Taylor and Francies.Google Scholar
Lapenta, G. & Markidis, S. 2011 Particle acceleration and energy conservation in particle in cell simulations. Phys. Plasmas 18 (7), 072101.Google Scholar
Melzani, M., Winisdoerffer, C., Walder, R., Folini, D., Favre, J. M., Krastanov, S. & Messmer, P. 2013 Apar-T: code, validation, and physical interpretation of particle-in-cell results. Astron. Astrophys. 558, A133.Google Scholar
Qiang, J.2017 High order numerical integrators for relativistic charged particle tracking. arXiv:1702.04486.Google Scholar
Uzan, J. P. & Deruelle, N. 2014 Théories de la Relativité. Belin.Google Scholar
Vay, J.-L. 2008 Simulation of beams or plasmas crossing at relativistic velocitya. Phys. Plasmas 15 (5), 056701.Google Scholar
Vay, J.-L. & Godfrey, B. B. 2014 Modeling of relativistic plasmas with the particle-in-cell method. C. R. Méc. 342 (10–11), 610–618.Google Scholar