Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-21T23:46:02.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Tokamak elongation – how much is too much? Part 1. Theory

Part of: Focus on Fusion PLA Tribute to V D Shafranov: 1929-2014

Published online by Cambridge University Press:  11 December 2015

J. P. Freidberg ,
A. Cerfon  and
J. P Lee
J. P. Freidberg
Affiliation:
Plasma Science and Fusion Center, MIT, Cambridge MA, USA
A. Cerfon
Affiliation:
Courant Institute of Mathematical Sciences, NYU, New York, NY, USA
J. P Lee*
Affiliation:
Plasma Science and Fusion Center, MIT, Cambridge MA, USA Courant Institute of Mathematical Sciences, NYU, New York, NY, USA
*
†Email address for correspondence: jungpyo@psfc.mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this and the accompanying paper, the problem of the maximally achievable elongation ${\it\kappa}$ in a tokamak is investigated. The work represents an extension of many earlier studies, which were often focused on determining ${\it\kappa}$ limits due to (i) natural elongation in a simple applied pure vertical field or (ii) axisymmetric stability in the presence of a perfectly conducting wall. The extension investigated here includes the effect of the vertical stability feedback system which actually sets the maximum practical elongation limit in a real experiment. A basic resistive wall stability parameter, 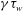${\it\gamma}{\it\tau}_{w}$, is introduced to model the feedback system which although simple in appearance actually captures the essence of the feedback system. 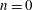Elongation limits in the presence of feedback are then determined by calculating the maximum ${\it\kappa}$ against $n=0$ resistive wall modes for fixed 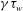${\it\gamma}{\it\tau}_{w}$. The results are obtained by means of a general formulation culminating in a variational principle which is particularly amenable to numerical analysis. The principle is valid for arbitrary profiles but simplifies significantly for the Solov’ev profiles, effectively reducing the 2-D stability problem into a 1-D problem. The accompanying paper provides the numerical results and leads to a sharp answer of ‘how much elongation is too much’?

Type
Research Article
Information
Journal of Plasma Physics , Volume 81 , Issue 6 , December 2015 , 515810607
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aymar, R., Barabaschi, P. & Shimomura, Y. 2002 The ITER design. Plasma Phys. Control. Fusion 44, 519–565.CrossRefGoogle Scholar
Bernard, L. C., Berger, D., Gruber, R. & Troyon, F. 1978 Axisymmetric MHD stability of elongated tokamaks. Nucl. Fusion 18, 1331–1336.Google Scholar
Cerfon, A. J. & Freidberg, J. P. 2010 ‘One size fits all’ analytic solutions to the Grad–Shafranov equation. Phys. Plasmas 17, 032502.CrossRefGoogle Scholar
Freidberg, J. P. 2014 Ideal MHD. Cambridge University Press.Google Scholar
Furth, H. P., Killeen, J. & Rosenbluth, M. N. 1963 Finite-resistivity instabilities of a sheet pinch. Phys. Fluids 6, 459–484.CrossRefGoogle Scholar
Grad, H. & Rubin, H. 1958 Hydromagnetic equilibria and force-free fields. In Proceedings of the 2nd United Nations Conference on the Peaceful Uses of Atomic Energy, vol. 31, pp. 190–197.Google Scholar
Haney, S. W. & Freidberg, J. P. 1989 Variational methods for studying tokamak stability in the presence of a thin resistive wall. Phys. Fluids B 1, 1637–1645.Google Scholar
Hutchinson, I. H., Boivin, R., Bombarda, F., Bonoli, P., Fairfax, S., Fiore, C., Goetz, J., Golovato, S., Granetz, R., Greenwald, M. et al. 1994 First results from Alcator-C-MOD. Phys. Plasmas 1, 1511–1518.Google Scholar
Kessel, C. E., Mau, T. K., Jardin, S. C. & Najmabadi, F. 2006 Plasma profile and shape optimization for the advanced tokamak power plant, ARIES-AT. Fusion Engng Des. 80, 63–77.Google Scholar
Lee, J. P., Cerfon, A., Freidberg, J. P. & Greenwald, M. 2015 Tokamak elongation – how much is too much? Part 2. Numerical results. J. Plasma Phys. 81, 515810608.Google Scholar
Miller, R. L., Chu, M. S., Greene, J. M., Lin-Liu, Y. R. & Waltz, R. E. 1998 Noncircular, finite aspect ratio, local equilibrium model. Phys. Plasmas 5, 973–978.Google Scholar
Najmabadi, F., The Aries Team: Bathke, C. G., Billone, M. C., Blanchard, J. P., Bromberg, L. Chin, E., Cole, F. R., Crowell, J. A., Ehst, D. A., El-Guebaly, L. A., Herring, J. S. et al.  1997 Overview of the ARIES-RS reversed-shear tokamak power plant study, Fusion Engng Des. 38, 3–25.Google Scholar
Najmabadi, F., The ARIES Team: Abdou, A., Bromberg, L., Brown, T., Chan, V. C., Chu, M. C., Dahlgren, F., El-Guebaly, L., Heitzenroeder, P., Henderson, D., St. John, H. E. et al.  2006 The ARIES-AT advanced tokamak, advanced technology fusion power plant, Fusion Engng Des. 80, 3–23.Google Scholar
Peng, Y.-K. M. & Strickler, D. J. 1986 Features of spherical torus plasmas. Nucl. Fusion 26, 769–777.Google Scholar
Roberto, M. & Galvão, R. M. O. 1992 ‘Natural elongation’ of spherical tokamaks. Nucl. Fusion 32, 1666–1669.Google Scholar
Sabbagh, S. A., Kaye, S. M., Menard, J., Paoletti, F., Bell, M., Bell, R. E., Bialek, J. M., Bitter, M., Fredrickson, E. D., Gates, D. A. et al. & NSTX Research Team 2001 Equilibrium properties of spherical torus plasmas in NSTX. Nucl. Fusion 41, 1601–1611.Google Scholar
Schissel, D. P., DeBoo, J. C., Burrell, K. H., Ferron, J. R., Groebner, R. J., St. John, H., Stambaugh, R. D., Tubbing, B. J. D., Thomsen, K., Cordey, J. G. et al. & JET Team 1991 H-mode energy confinement scaling from the DIII-D and JET tokamaks. Nucl. Fusion 31, 73–81.Google Scholar
Shafranov, V. D. 1958 On magnetohydrodynamical equilibrium configurations. Sov. Phys. JETP 6, 545.Google Scholar
Shi, B. 2005 Analytic description of high poloidal beta equilibrium with a natural inboard poloidal field null. Phys. Plasmas 12, 122504.Google Scholar
Sorbom, B. N., Ball, J., Palmer, T. R., Mangiarotti, F. J., Sierchio, J. M., Bonoli, P., Kasten, C. K., Sutherland, D. A., Barnard, H. S., Haakonsen, C. B. et al. 2015 ARC: a compact, high-field, fusion nuclear science facility and demonstration power plant with demountable magnets. Fusion Engng Des. 100, 378–405.CrossRefGoogle Scholar
Solov’ev, L. S. 1968 The theory of hydromagnetic stability of toroidal plasma configurations. Sov. Phys. JETP 26, 400–407.Google Scholar
Sykes, A., Ahn, J.-W., Akers, R., Arends, E., Carolan, P. G., Counsell, G. F., Fielding, S. J., Gryaznevich, M., Martin, R., Price, M. et al. & MAST Team 2001 First physics results from the MAST Mega-Amp Spherical Tokamak. Phys. Plasmas 8, 2101–2106.Google Scholar
Weening, R. H. 2000 Analytic spherical torus plasma equilibrium model. Phys. Plasmas 7, 3654–3662.CrossRefGoogle Scholar
Wesson, J. A. 1978 Hydromagnetic stability of tokamaks. Nucl. Fusion 18, 87–132.CrossRefGoogle Scholar
Zheng, S. B., Wootton, A. J. & Solano, E. R. 1996 Analytical tokamak equilibrium for shaped plasmas. Phys. Plasmas 3, 1176–1178.CrossRefGoogle Scholar