Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2025-01-01T19:55:52.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohen reals from small forcings

Published online by Cambridge University Press:  12 March 2014

Janusz Pawlikowski
Janusz Pawlikowski*
Affiliation:
Department of Mathematics, University of Wroclaw, PL. Grunwaldzki 2/4, 50-384 Wroclaw, Poland
*
Department of Mathematics, West Virginia University, Morgantown, WV 26506-6310, USA, E-mail: pawlikow@math.uni.wroc.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a new cardinal characteristic r*. related to the reaping number r. and show that

• posets of size < r* which add reals add unbounded reals;

• posets of size < r which add unbounded reals add Cohen reals.

We also show that add(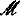) ≤ min(r. r*). It follows that posets of size < add(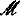) which add reals add Cohen reals.

This improves results of Roslanowski and Shelah [RS] and of Zapletal [Z].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 1 , March 2001 , pp. 318 - 324
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[AS]Abraham, U. and Shelah, S., Forcing closed unbounded sets, this Journal, vol. 48 (1983), pp. 643–657.Google Scholar
[BJ]Bartoszyński, T. and Judah, H., Set theory, On the structure of the real line, A. K. Peters, Wellesley, MA, 1995.Google Scholar
[CKP]Cichoń, J., Kamburelis, A., and Pawlikowski, J., On dense subsets of the measure algebra, Proceedings of the American Mathematical Society, vol. 94 (1985), pp. 142–146.CrossRefGoogle Scholar
[CP]Cichoń, J. and Pawlikowski, J., On ideals of subsets of the plane and on Cohen reals, this Journal, vol. 51 (1986), pp. 560–569.Google Scholar
[E]Eggleston, H. G., Two measure properties of cartesian product sets, The Quarterly Journal of Mathematics, (1954), no. 5, pp. 108–115.CrossRefGoogle Scholar
[KT]Kunen, K. and Tall, F. D., Between Martin's Axiom and Souslin's Hypothesis, Fundamenta Mathematicae vol. 102 (1979), pp. 173–181.CrossRefGoogle Scholar
[M]Miller, A. W., Some properties of measure and category, Transactions of the American Mathematical Society, vol. 266 (1981), pp. 93–114.CrossRefGoogle Scholar
[RS]Roslanowski, A. and Shelah, S., Simple forcing notions and forcing axioms, this Journal, to appear.Google Scholar
[S]Shelah, S., Can you take Solovay's inaccessible away, Israel Journal of Mathematics, vol. 48 (1984), pp. 1–47.CrossRefGoogle Scholar
[ST]Shelah, S. and Todorcevic, S., A note on small Baire spaces, Canadian Journal of Mathematics, vol. 63 (1986), pp. 659–665.CrossRefGoogle Scholar
[Z]Zapletal, J., Small forcings and Cohen reals, this Journal, vol. 62 (1997), pp. 280–284.Google Scholar