Article contents
Countable functionals and the projective hierarchy
Published online by Cambridge University Press: 12 March 2014
Extract
Kleene [7] and Kreisel [8] defined independently the countable (continuous) functionals. Kleene [7] defined the countable functionals of type k to be total functionals of type k acting in a continuous way when restricted to countable arguments of type k − 1. He also defined the associates for countable functionals. They are functions α: N → N containing information about how the functional acts on countable arguments. Kleene [7] showed that the countable functionals are closed under the computations derived from S1–S9 of his paper [6], and that every computable functional has a recursive associate.
Kreisel defined the continuous functionals to be equivalence-classes of associates. By his definition it is meaningless to let a continuous functional act upon anything but continuous arguments.
One disadvantage of Kleene's approach is that two different functionals may have the same associates We will later see that there may be two functionals φ1 and φ2 with the same associates but such that the relations
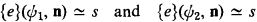
are not the same.
In more recent papers on the countable functionals it is normal to regard the hierarchy 〈Ct(k)〉kϵN of countable functionals as a type-structure such that the functionals in Ct(k + 1) are maps from Ct(k) to N(Ct(0) = N), see e.g. Bergstra [1] and Gandy and Hyland [3].
We will then enjoy the streamlined formalism of a type-structure in which S1–S9 have meaning, but avoid the ambiguities of Kleene's original approach.
We will presuppose a brief familiarity with the theory of the countable functionals.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
References
REFERENCES
- 6
- Cited by

