The Genericity Conjecture, as stated in Beller-Jensen-Welch [1], is the following:

(*) If O# ∉ L[R], R ⊆ ω, then R is generic over L.

We must be precise about what is meant by “generic”.

Definition (Stated in Class Theory). A generic extension of an inner model M is an inner model M[G] such that for some forcing notion 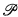⊆ M:

(a) 〈M, 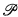〉 is amenable and ⊩ 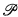is 〈M, 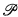〉-definable for 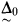sentences.

(b) G ⊆ 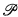is compatible, closed upwards, and intersects every 〈M, 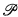〉-definable dense D ⊆ .

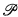A set x is generic over M if it is an element of a generic extension of M. And x is strictly generic over M if M[x] is a generic extension of M.

Though the above definition quantifies over classes, in the special case where M = L and O# exists, these notions are in fact first order, as all L-amenable classes are 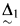definable over L[O#]. From now on assume that O# exists.

Theorem A. The Genericity Conjecture is false.

The proof is based upon the fact that every real generic over L obeys a certain definability property, expressed as follows.

Fact. If R is generic over L, then for some L-amenable class A, Sat〈L, A〉 is not definable over 〈L[R],A〉, where Sat〈L,A〉 is the canonical satisfaction predicate for 〈L,A〉.