Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schimmerling, Ernest
2010.
Handbook of Set Theory.
p.
1685.
Mitchell, William J.
2010.
Handbook of Set Theory.
p.
1497.
Ikegami, Daisuke
2010.
Forcing absoluteness and regularity properties.
Annals of Pure and Applied Logic,
Vol. 161,
Issue. 7,
p.
879.
Ben-Neria, Omer
2015.
The structure of the Mitchell order – II.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 12,
p.
1407.
Gitik, Moti
2020.
On κ-compact cardinals.
Israel Journal of Mathematics,
Vol. 237,
Issue. 1,
p.
457.
Fernandes, Gabriel
and
Schindler, Ralf
2021.
Tall Cardinals in Extender Models.
Notre Dame Journal of Formal Logic,
Vol. 62,
Issue. 3,
GITIK, MOTI
and
KAPLAN, EYAL
2023.
ON RESTRICTIONS OF ULTRAFILTERS FROM GENERIC EXTENSIONS TO GROUND MODELS.
The Journal of Symbolic Logic,
Vol. 88,
Issue. 1,
p.
169.
Gitik, Moti
and
Kaplan, Eyal
2023.
Non-stationary support iterations of Prikry forcings and restrictions of ultrapower embeddings to the ground model.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 1,
p.
103164.
Benhamou, Tom
Gitik, Moti
and
Hayut, Yair
2024.
The variety of projections of a tree Prikry forcing.
Journal of Mathematical Logic,
Vol. 24,
Issue. 03,
Gitik, Moti
2024.
Around accumulation points and maximal sequences of indiscernibles.
Archive for Mathematical Logic,
Vol. 63,
Issue. 5-6,
p.
591.
HOLLAND, JAMES
2024.
WEAK INDESTRUCTIBILITY AND REFLECTION.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 3,
p.
980.
GITIK, MOTI
and
KAPLAN, EYAL
2025.
ON EASTON SUPPORT ITERATION OF PRIKRY-TYPE FORCING NOTIONS.
The Journal of Symbolic Logic,
Vol. 90,
Issue. 3,
p.
968.
Kaplan, Eyal
2025.
The Magidor iteration and restrictions of ultrapowers to the ground model.
Israel Journal of Mathematics,
Vol. 265,
Issue. 2,
p.
605.
Benhamou, Tom
Garti, Shimon
Gitik, Moti
and
Poveda, Alejandro
2025.
Non-Galvin filters.
Journal of Mathematical Logic,
Vol. 25,
Issue. 02,

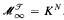 . Moreover, if there exists an elementary embedding π:
. Moreover, if there exists an elementary embedding π: 