Hostname: page-component-5c6d5d7d68-vt8vv Total loading time: 0.001 Render date: 2024-08-16T21:15:34.930Z Has data issue: false hasContentIssue false
  • English
  • Français

Major subspaces of recursively enumerable vector spaces1

Published online by Cambridge University Press:  12 March 2014

Iraj Kalantari
Iraj Kalantari*
Affiliation:
University of California, Santa Barbara, CA 93106
Get access Rights & Permissions [Opens in a new window]

Extract

The main point of this paper is a further development of some aspects of the recent theory of recursively enumerable (r.e.) algebraic structures. Initial work in this area is due to Frölich and Shepherdson [4] and Rabin [10]. Here we are only concerned with vector space structure. The previous work on r.e. vector spaces is due to Dekker [2], [3], Metakides and Nerode [8], Remmel [11], Retzlaff [13], and the author [5].

Our object of study is V∞ a countably infinite dimensional fully effective vector space over a countable recursive field 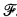. By fully effective we mean that V∞. under a fixed Godel numbering has the following properties:

(i) Operations of vector addition and scalar multiplication on V∞ are presented by partial recursive functions on the Gödel numbers of elements of V∞.

(ii) V∞ has a dependence algorithm, i.e., there is a uniform effective procedure which applied to any n vectors of V∞ determines whether or not they are linearly independent.

We also study 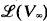, the lattice of r.e. subspaces of V∞ (under the operations of intersection, ⋂ and (weak) sum, +). We note that if 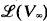is not distributive and is merely modular (see [1]). This fact indicates the essential difference between 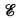the lattice of r.e. sets and .

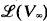Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 2 , June 1978 , pp. 293 - 303
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

These results form part of the author's dissertation.

References

BIBLIOGRAPHY

[1]Birkhoff, G., Lattice theory, American Mathematical Society, Colloquium Publications, no. 25, American Mathematical Society, Providence, Rhode Island, revised edition, 1967.Google Scholar
[2]Dekker, J. C. E., Countable vector spaces with recursive operations. Part I, this Journal, vol. 34 (1969), pp. 363–387.Google Scholar
[3]Dekker, J. C. E., Countable vector spaces with recursive operations. Part II, this Journal, vol. 36 (1971), pp. 477–495.Google Scholar
[4]Frölich, A. and Shepherdson, J. C., Effective procedures in field theory, Philosophical Transactions of the Royal Society of London. Series A, vol. 284 (1955), pp. 407–432.Google Scholar
[5]Kalantari, I., Structural properties of the lattice of recursively enumerable spaces, Ph.D. Dissertation, Cornell University, Ithaca, N.Y., 1976.Google Scholar
[6]Kalantari, I. and Retzlaff, A., Maximal vector spaces under automorphisms of the lattice of r.e. vector spaces, this Journal, vol. 42 (1977), pp. 481–491.Google Scholar
[7]Lachlan, A. H., On the lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 130 (1968), pp. 1–37.CrossRefGoogle Scholar
[8]Metakides, G. and Nerode, A., Recursively enumerable vector spaces, Annals of Mathematical Logic, vol. 11 (1977), pp. 147–171.CrossRefGoogle Scholar
[9]Post, E. L., Recursively enumerable sets of positive integers and their decision problems, Bulletin of the American Mathematical Society, vol. 50 (1944), pp. 284–316.CrossRefGoogle Scholar
[10]Rabin, M. O., Computable algebra, general theory and theory of computable fields, Transactions of the American Mathematical Society, vol. 95 (1960), pp. 341–360.Google Scholar
[11]Remmel, J., Co-recursively enumerable structures, Ph.D. Dissertation, Cornell University, Ithaca, N.Y., 1974.Google Scholar
[12]Remmel, J., On the vector spaces with no extendible basis, this Journal (to appear).Google Scholar
[13]Retzlaff, A., Recursive and simple spaces, Ph.D. Dissertation, Cornell University, Ithaca, N.Y., 1976.Google Scholar
[14]Soare, R. I., Automorphisms of the lattice of recursively enumerable sets. Part I: Maximal sets, Annals of Mathematics, vol. 100 (1974), pp. 80–120.CrossRefGoogle Scholar