Research Article
Prime and atomic models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 385-393
-
- Article
- Export citation
On the inconsistency of systems similar to

-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-2
-
- Article
- Export citation
Type two partial degrees1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 623-629
-
- Article
- Export citation
Ordinals connected with formal theories for transfinitely iterated inductive definitions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 161-182
-
- Article
- Export citation
On the compactness of ℵ1 and ℵ2
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 394-401
-
- Article
- Export citation
Toward model theory through recursive saturation1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 183-206
-
- Article
- Export citation
The perfect set theorem and definable wellorderings of the continuum
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 630-634
-
- Article
- Export citation
First steps in intuitionistic model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 3-12
-
- Article
- Export citation
Formalisations of further ℵ0-valued Łukasiewicz propositional calculi
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 207-210
-
- Article
- Export citation
Controlling the dependence degree of a recursively enumerable vector space1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 13-22
-
- Article
- Export citation
Cardinal collapsing and ordinal definability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 635-642
-
- Article
- Export citation
A characterization of companionable, universal theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 402-429
-
- Article
- Export citation
A sequent calculus formulation of type assignment with equality rules for the λβ-calculus
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 643-649
-
- Article
- Export citation
Relativized realizability in intuitionistic arithmetic of all finite types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 23-44
-
- Article
- Export citation
A r-maximal vector space not contained in any maximal vector space
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 430-441
-
- Article
- Export citation
An incomplete nonnormal extension of S3
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 211-212
-
- Article
- Export citation
Degrees of sensible lambda theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 45-55
-
- Article
- Export citation
Examples in the theory of existential completeness
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 650-658
-
- Article
- Export citation
A type-free Gödel interpretation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 213-227
-
- Article
- Export citation
Theories with a finite number of countable models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 442-455
-
- Article
- Export citation

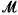 of
of 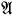 is said to be
is said to be 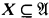 and every elementary monomorphism on
and every elementary monomorphism on 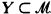 . This notion is used in a variety of ways in model theory. It aids in distinguishing between models that are not isomorphic, as in Vaught [10]. It also aids in showing that certain models
. This notion is used in a variety of ways in model theory. It aids in distinguishing between models that are not isomorphic, as in Vaught [10]. It also aids in showing that certain models 
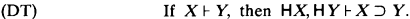

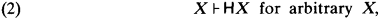

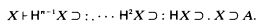
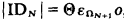 , where ID
, where ID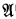 [X,
[X,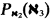 are not normal, and that the method cannot be extended to show that ℵ
are not normal, and that the method cannot be extended to show that ℵ
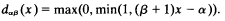
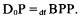
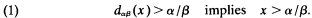
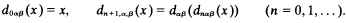
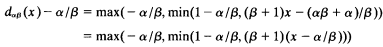
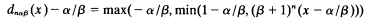
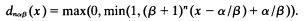
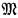 be a transitive model of set theory with the axiom of choice. Definability of sets in the generic extensions of
be a transitive model of set theory with the axiom of choice. Definability of sets in the generic extensions of  is the λ-theory axiomatized by the set {
is the λ-theory axiomatized by the set {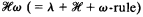 is Π
is Π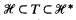 and 2
and 2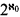 .
.