Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kossak, Roman
1991.
A correction to: “On extensions of models of strong fragments of arithmetic” [Proc. Amer. Math. Soc. 108 (1990), no. 1, 223–232; MR0984802 (90d:03123)].
Proceedings of the American Mathematical Society,
Vol. 112,
Issue. 3,
p.
913.
Li, Wei
2014.
Δ2 degrees without Σ1 induction.
Israel Journal of Mathematics,
Vol. 201,
Issue. 2,
p.
989.
Kurahashi, Taishi
and
Minami, Yoshiaki
2024.
On collection schemes and Gaifman's splitting theorem.
Mathematical Logic Quarterly,
Vol. 70,
Issue. 4,
p.
398.

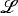 = {0,1, +,·,<} be the usual first-order language of arithmetic. We show that Peano arithmetic is the least first-order
= {0,1, +,·,<} be the usual first-order language of arithmetic. We show that Peano arithmetic is the least first-order 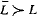 and
and 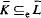 such that
such that 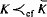 .
.