In this note we present a simplification of the axiom schemes which were given in our earlier paper Axiom schemes for m-valued propositional calculi. Except for new concepts that are needed for our present purposes, the terminology used will be the same as that introduced in the earlier paper. Hence, we can say that in addition to listing our simplified specifications for axiom schemes, we shall indicate how our new axiom schemes may be used to establish deductive completeness.

The simplification of our axiom schemes is achieved by using only the operators ⊃ and Jk( ) with the resulting elimination of ∨ and ·. This does not constitute an actual reduction in functional complexity since the latter operators can be denned in terms of the former. For example,

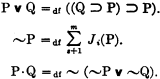
However, by dispensing with ∨ and · one can greatly reduce the number of axioms without an appreciable increase in the difficulties of proving deductive completeness.

Our simplified specifications for axiom schemes will retain conditions (1) and (3) of our earlier set but (2) and (4) will be changed to (2*) and (4*) which we will now state.

(2*) Assume that an implication function (P ⊃ Q) can be defined exclusively in terms of the basic functions Fi(P1, …:, Pαi).

The statement of what follows is simplified by introducing a chain symbol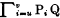 defined recursively as follows:

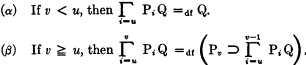
The variable i of a chain symbol which takes values from u to v will be called the chain variable. When it is clear that i is the chain variable we will use the notation 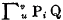in place of 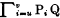. Hence, 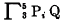denotes (P5 ⊃ (P4 ⊃ (P3 ⊃ Q))).