Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T00:03:07.837Z Has data issue: false hasContentIssue false
  • English
  • Français

On amalgamations of languages with Magidor-Malitz quantifiers

Published online by Cambridge University Press:  12 March 2014

Carl F. Morgenstern
Carl F. Morgenstern*
Affiliation:
University of California, Santa Cruz, California 95064
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we indicate how compact languages containing the Magidor-Malitz quantifiers Qκn in different cardinalities can be amalgamated to yield more expressive, compact languages.

The language Lκ<ω, originally introduced by Magidor and Malitz [9], is a natural extension of the language L(Q) introduced by Mostowski and investigated by Fuhrken [6], [7], Keisler [8] and Vaught [13]. Intuitively, Lκ<ω is first-order logic together with quantifiers Qκn (n ∈ ω) binding n free variables which express “there is a set X of cardinality κ such than any n distinct elements of X satisfy …”, or in other words, 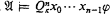iff the relation on 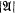determined by φ contains an n-cube of cardinality κ. With these languages one can express a variety of combinatorial statements of the type considered by Erdös and his colleagues, as well as concepts in universal algebra which are beyond the scope of first-order logic. The model theory of Lκ<ω has been further developed by Badger [1], Magidor and Malitz [10] and Shelah [12].

We refer to a language as being < κ compact if, given any set of sentences Σ of the language, if Σ is finitely satisfiable and ∣Σ∣ < κ, then Σ has a model. The phrase countably compact is used in place of <ℵ1 compact.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 4 , December 1979 , pp. 549 - 558
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Badger, L., The Malitz quantifier meets its Ehrenfeucht game, Ph.D. thesis, University of Colorado, 1975.Google Scholar
[2]Burgess, J., unpublished manuscript.Google Scholar
[3]Chang, C. C. and Keisler, J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[4]Drake, F., Set theory: An introduction to large cardinals, North-Holland, Amsterdam, 1974.Google Scholar
[5]Dushnik, B. and Miller, E. W., Partially ordered sets, American Journal of Mathematics, vol. 63(1941), pp. 600–610.CrossRefGoogle Scholar
[6]Fuhrken, G., Skolem-type normal forms for first order languages with a generalized quantifier, Fundamenta Mathematicae, vol. 54(1964), pp. 291–302.CrossRefGoogle Scholar
[7]Fuhrken, G., Languages with added quantifier “there exists at least ℵα”, The theory of models (Addison, J. W., Henkin, L., Tarski, A., Editors), North-Holland, Amsterdam, 1965, pp. 121–131.Google Scholar
[8]Keisler, J., Logic with the quantifier “there exists uncoimtably many”, Annals of Mathematical Logic, vol. 1(1970), pp. 1–93.CrossRefGoogle Scholar
[9]Magidor, M. and Malitz, J., Compact extensions of L(Q), Part 1a, Annals of Mathematical Logic, vol. 11(1977), pp. 217–261.CrossRefGoogle Scholar
[10]Magidor, M. and Malitz, J., Compactness and transfer for a fragment of L<ω, this Journal, vol. 42(1977), pp. 261–269.Google Scholar
[11]Mostowski, A., On a generalization of quantifiers, Fundamenta Mathematicae, vol. 44(1957), pp. 12–36.CrossRefGoogle Scholar
[12]Shelah, S., Various results in mathematical logic, Notices of the American Mathematical Society, vol. 24(1977), p. A–250.Google Scholar
[13]Vaught, R., The completeness of logic with the added quantifier “there are uncoimtably many”, Fundamenta Mathematicae, vol. 54(1964), pp. 303–304.CrossRefGoogle Scholar
[14]Vaught, R., A Löwenheim-Skolem theorem for cardinals far apart, The theory of models (Addison, J. W., Henkin, L., Tarski, A., Editors), North-Holland, Amsterdam, 1965, pp. 390–401.Google Scholar