Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-12T17:51:17.511Z Has data issue: false hasContentIssue false
  • English
  • Français

On Dedekind complete o-minimal structures

Published online by Cambridge University Press:  12 March 2014

Anand Pillay  and
Charles Steinhorn
Anand Pillay
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, Indiana 46556
Charles Steinhorn
Affiliation:
Department of Mathematics, Vassar College, Poughkeepsie, New York 12601
Get access Rights & Permissions [Opens in a new window]

Abstract

For a countable complete o-minimal theory T, we introduce the notion of a sequentially complete model of T. We show that a model 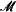of T is sequentially complete if and only if 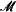≺ 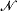for some Dedekind complete model 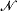. We also prove that if T has a Dedekind complete model of power greater than 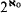, then T has Dedekind complete models of arbitrarily large powers. Lastly, we show that a dyadic theory—namely, a theory relative to which every formula is equivalent to a Boolean combination of formulas in two variables—that has some Dedekind complete model has Dedekind complete models in arbitrarily large powers.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 52 , Issue 1 , March 1987 , pp. 156 - 164
Copyright
Copyright © Association for Symbolic Logic 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Research partially supported by N.S.F. grant DMS 8401713.

2

Research partially supported by N.S.F. grant DMS 8403137.

References

REFERENCES

[1] Marker, D., Omitting types in -minimal theories, this Journal, vol. 51 (1986), pp. 63–74.Google Scholar
[2] Knight, J., Pillay, A. and Steinhorn, C., Definable sets in ordered structures. II, Transactions of the American Mathematical Society, vol. 295 (1986), pp. 593–605.CrossRefGoogle Scholar
[3] Pillay, A. and Steinhorn, C., Definable sets in ordered structures, Bulletin (New Series) of the American Mathematical Society, vol. 11 (1984), pp. 159–162.CrossRefGoogle Scholar
[4] Pillay, A. and Steinhorn, C., Definable sets in ordered structures. I, Transactions of the American Mathematical Society, vol. 295(1986), pp. 565–592.CrossRefGoogle Scholar
[5] Pillay, A. and Steinhorn, C., Definable sets in ordered structures. III, Transactions of the American Mathematical Society (submitted).Google Scholar