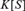Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pelupessy, Florian
2018.
Reverse mathematics of the finite downwards closed subsets of ordered by inclusion and adjacent Ramsey for fixed dimension.
Mathematical Logic Quarterly,
Vol. 64,
Issue. 3,
p.
178.
Carlucci, Lorenzo
Mainardi, Leonardo
and
Rathjen, Michael
2019.
Computing with Foresight and Industry.
Vol. 11558,
Issue. ,
p.
144.
Marcone, Alberto
2020.
Well-Quasi Orders in Computation, Logic, Language and Reasoning.
Vol. 53,
Issue. ,
p.
189.
Wu, Huishan
2023.
Structure of semisimple rings in reverse and computable mathematics.
Archive for Mathematical Logic,
Vol. 62,
Issue. 7-8,
p.
1083.
Bazhenov, Nikolay
Fiori-Carones, Marta
Liu, Lu
and
Melnikov, Alexander
2024.
Primitive recursive reverse mathematics.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 1,
p.
103354.