Article contents
Saturated ideals and the singular cardinal hypothesis
Published online by Cambridge University Press: 12 March 2014
Extract
The large cardinal-like properties of saturated ideals have been investigated by various authors, including Foreman [F], and Jech and Prikry [JP], among others. One of the most interesting consequences of a strongly compact cardinal is the following theorem of Solovay [So2]: if a strongly compact cardinal exists then the singular cardinal hypothesis holds above it. In this paper we discuss the question of relating the existence of saturated ideals and the singular cardinal hypothesis. We will show that the existence of “strongly” saturated ideals implies the singular cardinal hypothesis. As a biproduct we will present a proof of the above mentioned theorem of Solovay using generic ultrapowers. See Jech and Prikry [JP] for a nice exposition of generic ultrapowers. We owe a lot to the work of Foreman [F]. We would like to express our gratitude to Noa Goldring for many helpful comments and discussions.
Throughout this paper we assume that κ is a strongly inaccessible cardinal and λ is a cardinal >κ. By an ideal on 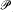 κλ we mean a κ-complete fine ideal on Pκλ. For I an ideal on
κλ we mean a κ-complete fine ideal on Pκλ. For I an ideal on 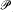 κλ let PI denote the poset of I-positive subsets of
κλ let PI denote the poset of I-positive subsets of 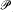 κλ.
κλ.
Definition. Let I be an ideal on 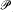 κλ. We say that I is a bounding ideal if 1 ⊩-PI “δ(δ is regular cardinal
κλ. We say that I is a bounding ideal if 1 ⊩-PI “δ(δ is regular cardinal 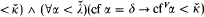 ”.
”.
We can show that if a normal ideal is “strongly” saturated then it is bounding.
Theorem 1. If 1 is an η-saturated normal ideal on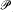 κλ, where η is a cardinal <λsuch that there are fewer thanκmany cardinals betweenκand η (i.e. η < κ+κ), then I is bounding.
κλ, where η is a cardinal <λsuch that there are fewer thanκmany cardinals betweenκand η (i.e. η < κ+κ), then I is bounding.
Proof. Let I be such an ideal on 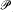 κλ. By the work of Foreman [F] and others, we know that every λ+-saturated normal ideal is precipitous. Suppose G is a generic filter for our PI. Let j: V → M be the corresponding generic elementary embedding. By a theorem of Foreman [F, Lemma 10], we know that Mλ ⊂ M in V[G]. By η-saturation, cofinalities ≥η are preserved; that is, if cfvα ≥ η, then cfvα = cfv[G]α. From j ↾ Vκ being the identity on Vκ and M being λ-closed in V[G], we conclude that cofinalities <κ are preserved. Therefore if cfvα ≠ cfv[G]α then κ ≤ cfvα < η.
κλ. By the work of Foreman [F] and others, we know that every λ+-saturated normal ideal is precipitous. Suppose G is a generic filter for our PI. Let j: V → M be the corresponding generic elementary embedding. By a theorem of Foreman [F, Lemma 10], we know that Mλ ⊂ M in V[G]. By η-saturation, cofinalities ≥η are preserved; that is, if cfvα ≥ η, then cfvα = cfv[G]α. From j ↾ Vκ being the identity on Vκ and M being λ-closed in V[G], we conclude that cofinalities <κ are preserved. Therefore if cfvα ≠ cfv[G]α then κ ≤ cfvα < η.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1992
References
REFERENCES
- 2
- Cited by


