Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-16T20:16:01.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Sequences of n-diagrams

Published online by Cambridge University Press:  12 March 2014

Valentina S. Harizanov ,
Julia F. Knight  and
Andrei S. Morozov
Valentina S. Harizanov
Affiliation:
Department of Mathematics, The George Washington University, Washington, D.C. 20052, USA, E-mail: harizanv@gwu.edu
Julia F. Knight
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, IN 46556, USA, E-mail: Knight.1@nd.edu
Andrei S. Morozov
Affiliation:
Sobolev Institute of Mathematics, Novosibirsk, 630090, Russia, E-mail: morozov@math.nsc.ru
Get access Rights & Permissions [Opens in a new window]

Extract

We consider only computable languages, and countable structures, with universe a subset of ω, which we think of as a set of constants. We identify sentences with their Gödel numbers. Thus, for a structure 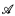, the complete (elementary) diagram, Dc(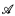), and the atomic diagram, D(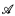), are subsets of ω. We classify formulas as usual. A formula is both Σ0 and Π0 if it is open. For n > 0, a formula, in prenex normal form, is Σn, or Πn, if it has n blocks of like quantifiers, beginning with ∃, or ∀. For a formula θ, in prenex normal form, we let neg(θ) denote the dual formula that is logically equivalent to ¬θ—if θ is Σn, then neg(θ) is Πn, and vice versa.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 3 , September 2002 , pp. 1227 - 1247
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ash, C., Knight, J., Manasse, M., and Slaman, T., Generic copies of countable structures, Annals of Pure and Applied Logic, vol. 42 (1989), pp. 195–205.CrossRefGoogle Scholar
[2]Ash, C. J. and Knight, J. F., Possible degrees in recursive copies II, Annals of Pure and Applied Logic, vol. 87 (1997), pp. 151–165.CrossRefGoogle Scholar
[3]Ash, C. J. and Knight, J. F., Computable Structures and the Hyperarithmetical Hierarchy, Elsevier, Amsterdam, 2000.Google Scholar
[4]Barwise, J., Back and forth through infinitary logic, Studies in Model Theory (Morley, M. D., editor), MAA Studies in Mathematics, vol. 8, Mathematical Association of America, Buffalo, New York, 1973, pp. 5–34.Google Scholar
[5]Chisholm, J., Effective model theory vs. recursive model theory, this Journal, vol. 55 (1990), pp. 1168–1191.Google Scholar
[6]Chisholm, J. and Moses, M., An undecidable linear order that is n-decidable for all n, Notre Dame Journal of Formal Logic, vol. 39 (1998), pp. 519–526.CrossRefGoogle Scholar
[7]Goncharov, S. S., Restricted theories of constructive Boolean algebras, Sibirskii Matematicheskii Zhurnal, vol. 17 (1976), pp. 797–812, Russian, pp. 601–611 (English translation).Google Scholar
[8]Knight, J. F., Models of arithmetic: quantifiers and complexity, to appear in volume on reverse mathematics (Simpson, S., editor).Google Scholar
[9]Knight, J. F., Sequences of degrees associated with models of arithmetic, to appear in Logic Colloquium 2001.Google Scholar
[10]Knight, J. F., Degrees coded in jumps of orderings, this Journal, vol. 51 (1986), pp. 1034–1042,Google Scholar
[11]Knight, J. F., Minimality and completions of PA, this Journal, vol. 66 (2001), pp. 1447–1457.Google Scholar
[12]Moses, M., n-recursive linear orders without (n + 1)-recursive copies, Logical Methods (Crossley, J. N., Remmel, J. B., Shore, R. A., and Sweedler, M. E., editors), BirkhÄuser, Boston, 1993, pp. 572–592.CrossRefGoogle Scholar