Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T02:24:04.686Z Has data issue: false hasContentIssue false
  • English
  • Français

A 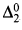set with barely degree

Published online by Cambridge University Press:  12 March 2014

Rod Downey ,
Geoffrey Laforte  and
Steffen Lempp
Rod Downey
Affiliation:
School of Mathematical and Computer Sciences, Victoria University, Po Box 600, Wellington, New Zealand, E-mail: rod.downey@vuw.ac.nz
Geoffrey Laforte
Affiliation:
Institute For Human and Machine Cognition, 11000 University Parkway, Pensacola. FL 32514, USA, E-mail: glaforte@ai.uwf.edu
Steffen Lempp
Affiliation:
Department of Mathematics, University of Wisconsin, 480 Lincoln Drive, Madison, WI 53706-1388, USA, E-mail: lempp@math.wisc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a 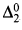degree which fails to be computably enumerable in any computably enumerable set strictly below .

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 4 , December 1999 , pp. 1700 - 1718
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arslanov, M., LaForte, G., and Slaman, T., Relative enumerability in the difference hierarchy, this Journal.Google Scholar
[2]Downey, R., The 0‴ priority method with special attention to density results, Recursion theory week: Proceedings, Oberwohlfach 1989 (Ambos-Spies, K.et al., editors), Springer, Berlin, 1990.Google Scholar
[3]Sacks, G., Recursive enumerability and the jump operator, Transactions of the American Mathematical Society, vol. 108 (1963), pp. 223–239.CrossRefGoogle Scholar
[4]Shore, R., A non-inversion theorem for the jump operator, Annals of Pure and Applied Logic, vol. 40 (1988), pp. 277–303.CrossRefGoogle Scholar
[5]Soare, R., Recursively enumerable sets and degrees, Springer, Berlin, 1987.CrossRefGoogle Scholar