Article contents
A splitting theorem for simple Π11 Sets
Published online by Cambridge University Press: 12 March 2014
Extract
As was first mentioned in [3, §5], if A is any 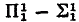 –
– 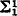 set, A is the union of two disjoint
set, A is the union of two disjoint 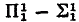 –
– 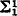 sets B(0), B(1). In metarecursion theory this is proven as follows. Let ƒ be a one-to-one metarecursive function whose range is A, let R be an unbounded metarecursive set whose complement is also unbounded, and set B(0) = f(R), B(1) = f(
sets B(0), B(1). In metarecursion theory this is proven as follows. Let ƒ be a one-to-one metarecursive function whose range is A, let R be an unbounded metarecursive set whose complement is also unbounded, and set B(0) = f(R), B(1) = f(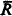 ). The corresponding fact of ordinary recursion theory, namely that any r.e. but not recursive set can be split into two other such sets, was proved by Friedberg [2, Theorem 1], using a clever priority argument. Sacks [7, Corollary 2] then showed that any r.e. but not recursive set is the union of two disjoint r.e. sets neither of which was recursive in the other, a much stronger result. In this paper we attempt to prove the analogous result for
). The corresponding fact of ordinary recursion theory, namely that any r.e. but not recursive set can be split into two other such sets, was proved by Friedberg [2, Theorem 1], using a clever priority argument. Sacks [7, Corollary 2] then showed that any r.e. but not recursive set is the union of two disjoint r.e. sets neither of which was recursive in the other, a much stronger result. In this paper we attempt to prove the analogous result for 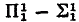 –
– 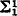 sets A, but succeed only in the case A is simple; i.e., the complement of A contains no infinite
sets A, but succeed only in the case A is simple; i.e., the complement of A contains no infinite 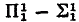 subset. As a corollary we show the
subset. As a corollary we show the 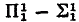 metadegrees are dense, a fact already announced by Sacks [8, Corollary 1], but only proven by him for nonzero
metadegrees are dense, a fact already announced by Sacks [8, Corollary 1], but only proven by him for nonzero 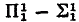 metadegrees.
metadegrees.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
References
- 3
- Cited by


