Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-25T06:49:55.935Z Has data issue: false hasContentIssue false
  • English
  • Français

Systems of notations and the ramified analytical hierarchy

Published online by Cambridge University Press:  12 March 2014

Joan D. Lukas  and
Hilary Putnam
Joan D. Lukas
Affiliation:
University of Massachusetts, Boston, Massachusetts 02116
Hilary Putnam
Affiliation:
Harvard University, Cambridge, Massachusetts 02138
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of this paper is to show that arithmetically minimal systems of notations can be constructed which provide notations for all ramified analytical ordinals (all the ordinals in the minimum β-model for analysis). This is a much larger section of the second number class than the Church-Kleene constructive ordinals (although still only an initial segment of the 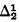ordinals). Arithmetic minimality means that if H is an “H-set” associated with an ordinal α in our system and H′ is an H-set associated with the same ordinal α in an arbitrary system of notations S, then H is arithmetical in H′. Thus the arithmetical degrees associated with ordinals in our system are as low as possible.

In order to clarify the structure of degrees of unsolvability and, more generally, to gain a deeper insight into the power set of the integers, coarser but neater classifications than the structure of Turing degrees have been sought. Several hierarchies of sets of integers have been studied, each of which organizes a certain class of sets (or their degrees of unsolvability) into a well-ordering of levels with increasing complexity of nonrecursiveness appearing at each new level. The best known of these hierarchies is the Kleene hierarchy of arithmetical sets.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 39 , Issue 2 , June 1974 , pp. 243 - 253
Copyright
Copyright © Association for Symbolic Logic 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Boolos, G. and Putnam, Hilary, Degrees of unsolvability of constructible sets of integers, this Journal, vol. 33 (1968), pp. 497–513.Google Scholar
[2] Boyd, R., Hensel, G. and Putnam, H., A recursion-theoretic characterization of the ramified analytical hierarchy, Transactions of the American Mathematical Society, vol. 141 (1969), pp. 37–62.CrossRefGoogle Scholar
[3] Cohen, P. J., A minimal model for set theory, Bulletin of the American Mathematical Society, vol. 3 (1964), pp. 537–540.Google Scholar
[4] Enderton, H. B., Hierarchies in recursive function theory, Transactions of the American Mathematical Society, vol. III (1964), pp. 457–471.CrossRefGoogle Scholar
[5] Enderton, H. B. and Putnam, H., A note on the hyperarithmetical hierarchy, this Journal, vol. 35 (1970), pp. 429–430.Google Scholar
[6] Gödel, K., Consistency proof for the generalized continuum hypothesis, Proceedings of the National Academy of Science, U.S.A., vol. 251 (1939), pp. 220–224.CrossRefGoogle Scholar
[7] Luckham, D. and Putnam, H., On minimal and almost-minimal systems of notations, Transactions of the American Mathematical Society, vol. 119 (1965), pp. 86–100.CrossRefGoogle Scholar
[8] Lukas, J. D., Systems of notations and the constructible-hierarchy, Doctoral Dissertation, Massachusetts Institute of Technology, Cambridge, Mass., 1967.Google Scholar
[9] Rogers, H. Jr., The theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[10] Spector, C., Recursive well-orderings, this Journal, vol. 20 (1955), pp. 151–163.Google Scholar
[11] Spector, C., On degrees of recursive unsolvability, Annals of Mathematics, vol. 64 (1956), pp. 581–592.CrossRefGoogle Scholar