Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-12T22:57:58.961Z Has data issue: false hasContentIssue false
  • English
  • Français

T-convexity and tame extensions II

Published online by Cambridge University Press:  12 March 2014

Lou van den Dries
Lou van den Dries*
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61820, USA, E-mail: vddries@symcom.math.uiuc.edu
Get access Rights & Permissions [Opens in a new window]

Extract

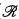I solve here some problems left open in “T-convexity and Tame Extensions” [9]. Familiarity with [9] is assumed, and I will freely use its notations. In particular, T will denote a complete o-minimal theory extending RCF, the theory of real closed fields. Let (, V) ⊨ Tconvex, let 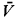= V/m(V) be the residue field, with residue class map x ↦ 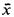: V ↦ 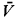, and let υ: 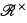→ Γ be the associated valuation. “Definable” will mean “definable with parameters”. The main goal of this article is to determine the structure induced by (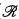, V) on its residue field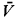and on its value group Γ. In [9] we expanded the ordered field 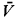to a model of T as follows. Take a tame elementary substructure 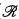′ of 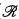such that R′ ⊆ V and R′ maps bijectively onto 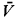under the residue class map, and make this bijection into an isomorphism 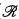′ ≌ 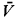of T-models. (We showed such ′ exists, and that this gives an expansion of 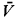to a T-model that is independent of the choice of ′.).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 1 , March 1997 , pp. 14 - 34
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bröcker, L., On the reduction of semialgebraic sets by real valuations, Recent advances in real algebraic geometry and quadratic forms (Jacob, W. B., Lam, T.-Y., and Robson, R. O., editors), Contemporary Mathematics, vol. 155, 1994, pp. 75–95.CrossRefGoogle Scholar
[2] Holly, J., Canonical forms for definable subsets of algebraically closed and real closed valuedfields, this Journal, vol. 60 (1995), pp. 843–860.Google Scholar
[3] Kuhlmann, F.-V. and Kuhlmann, S., On the structure of nonarchimedean exponential fields II, Communications in Algebra, vol. 22 (1994), pp. 5079–5103.CrossRefGoogle Scholar
[4] Loveys, J. and Peterzil, Y., Linear o-minimal structures, Israel Journal of Mathematics, vol. 81 (1993), pp. 1–30.CrossRefGoogle Scholar
[5] Marker, D. and Steinhorn, C., Definable types in o-minimal theories, this Journal, vol. 59 (1994), pp. 185–198.Google Scholar
[6] Miller, C., A growth dichotomy for o-minimal expansions of orderedfields, Logic: from foundations to applications (European Logic Colloquium, 1993, Hodges, W., Hyland, J., Steinhorn, C., and Truss, J., editors), Oxford University Press, 1996, pp. 385–399.CrossRefGoogle Scholar
[7] Miller, C., Exponentiation is hard to avoid, Proceedings of the American Mathematical Society, vol. 122 (1994), pp. 257–259.CrossRefGoogle Scholar
[8] Pillay, A., Definability of types, and pairs of o-minimal structures, this Journal, vol. 59 (1994), pp. 1400–1409.Google Scholar
[9] van den Dries, L. and Lewenberg, A. H., T-convexity and tame extensions, this Journal, vol. 60 (1995), pp. 74–102.Google Scholar
[10] van den Dries, L., Macintyre, A., and Marker, D., The elementary theory of restricted analytic fields with exponentiation, Annals of Mathematics, vol. 140 (1994), pp. 183–205.CrossRefGoogle Scholar
[11] Wilkie, A., Model completeness for expansions of the real field by restricted Pfaffian functions and by the exponential function, to appear in Journal of the American Mathematical Society.Google Scholar