Article contents
Transfinite extensions of Friedberg's completeness criterion1
Published online by Cambridge University Press: 12 March 2014
Extract
In [3] Friedberg showed that every Turing degree ≥ 0′ is the jump of some degree. Using the relativized version of this theorem it can be shown by finite induction that if a ≥ 0(n)0(n) then there is a b such that b(n) = a (our notation is defined in §1). It is natural to ask whether these results can be extended into the transfinite. Is it true for example, that whenever a ≥ 0(ω) there is a b such that = b(ω)= a? In §2 we use forcing to prove this result. (The usefulness of forcing in answering questions involving the jump operation on degrees of unsolvability has been previously demonstrated in Selman [5] where, for example, forcing was used to construct degrees a and b such that a(ω) = b(ω) = a ∪ b = 0(ω).) In §3 we generalize the methods of §2 to show that if α is a recursive ordinal and a ≥ 0(α) then there is a bsuch that b(α) = a, i.e. the Friedberg result can be extended to all recursive ordinal levels.
Thomason [6] used a forcing argument to show: If 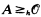 (the Kleene set of notations for the recursive ordinals) then there is a B such that
(the Kleene set of notations for the recursive ordinals) then there is a B such that 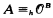 (the set of notations for ordinals recursive in B). In §4 we show this result holds when hyperarithmetic reducibility is replaced by Turing reducibility: If
(the set of notations for ordinals recursive in B). In §4 we show this result holds when hyperarithmetic reducibility is replaced by Turing reducibility: If 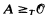 then there is a B such that
then there is a B such that 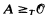 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1977
Footnotes
This work was partially supported by NSF Grant GP–29079.
References
BIBLIOGRAPHY
- 8
- Cited by

