Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-05T12:40:55.935Z Has data issue: false hasContentIssue false
  • English
  • Français

A transfinite sequence of ω-models

Published online by Cambridge University Press:  12 March 2014

Andrzej Mostowski
Andrzej Mostowski*
Affiliation:
University of Warsaw, Warsaw, Poland
Get access Rights & Permissions [Opens in a new window]

Extract

Let A2 be the axiomatic system of second order arithmetic as described in [2]. One of the models of A2 is the “principal model” Mpr consisting of all integers and all sets of integers. Obviously there exist many denumerable ω-models elementarily equivalent to Mpr and we shall deal in this paper with some questions pertaining to this family which we denote by .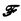

In §1 we define a rather natural relation ε between two denumerable families of sets of integers. From the upward Skolem-Löwenheim theorem it follows easily that there exists a family 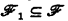ordered by ε in the type ω1, but it is not immediately obvious whether there exist a subfamily of 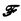not well-ordered by ε. In the present paper we construct such a family of type η. ω1 where η is the order type of rationals and indicate some applications to hyperdegrees.

We adopt the terminology and notation of [2], with the only change that we adjoin to the language of A2 the constants ν0, ν1, … for the consecutive numerals 0, 1, 2, … and axioms which characterise them:

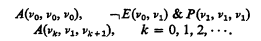
Also we modify the axioms of A2 given in [2] by prefixing them by general quantifiers bounded either to S or to N.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 1 , March 1972 , pp. 96 - 102
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Grzegorczyk, A., Mostowski, A. and Ryll-Nardzewski, Cz., The classical and the ω-complete arithmetic, this Journal, vol. 23 (1958), pp. 188–206.Google Scholar
[2]Mostowski, A. and Suzuki, Y., On ω-models which are not β-models, Fundamenta Mathematicae, vol. 65 (1969), pp. 83–93.CrossRefGoogle Scholar
[3]Shoenheld, J. R., Mathematical Logic, Addison-Wesley, Reading, Massachusetts, 1967.Google Scholar
[4]Keisler, H. J., Model theory for infinitary logic, North-Holland, Amsterdam, 1971.Google Scholar
[5]Thomason, S. K., The forcing method and the upper semilattice of hyperdegrees, Transactions of the American Mathematical Society, vol. 129 (1967), pp. 38–57.CrossRefGoogle Scholar