An Ax-Kochen-Ershov principle for intermediate structures between valued groups and valued fields.

We will consider structures that we call valued B-groups and which are of the form 〈G, B, *, υ〉 where

– G is an abelian group,

– B is an ordered group,

– υ is a valuation denned on G taking its values in B,

– * is an action of B on G satisfying: ∀x ϵ G ∀ b ∈ B υ(x * b) = ν(x) · b.

The analysis of Kaplanski for valued fields can be adapted to our context and allows us to formulate an Ax-Kochen-Ershov principle for valued B-groups: we axiomatise those which are in some sense existentially closed and also obtain many of their model-theoretical properties. Let us mention some applications:

1. Assume that υ(x) = υ(nx) for every integer n ≠ 0 and x ϵ G, B is solvable and acts on G in such a way that, for the induced action, Z[B] ∖ {0} embeds in the automorphism group of G. Then 〈G, B, *, υ〉 is decidable if and only if B is decidable as an ordered group.

2. Given a field k and an ordered group B, we consider the generalised power series field k((B)) endowed with its canonical valuation. We consider also the following structure:

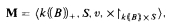
where k((B))+ is the additive group of k((B)), S is a unary predicate interpreting {Tb ∣ b ϵB}, and ×↾k((B))×S is the multiplication restricted to k((B)) × S, structure which is a reduct of the valued field k((B)) with its canonical cross section. Then our result implies that if B is solvable and decidable as an ordered group, then M is decidable.

3. A valued B–group has a residual group and our Ax-Kochen-Ershov principle remains valid in the context of expansions of residual group and value group. In particular, by adding a residual order we obtain new examples of solvable ordered groups having a decidable theory.