Article contents
Uniform inductive definability and infinitary languages
Published online by Cambridge University Press: 12 March 2014
Extract
Introduction. The purpose of this paper is to show how results from the theory of inductive definitions can be used to obtain new compactness theorems for uncountable admissible languages. These will include improvements of the compactness theorem by J. Green [9].
In [2] Barwise studies admissible sets satisfying the Σ1-compactness theorem. Our approach is to consider admissible sets satisfying what could be called the abstract extended completeness theorem, that is, sets where the consequence relation of the admissible fragment LA is Σ1-definable over A. We will call such sets Σ1-complete. For countable admissible sets, Σ1-completeness follows from the completeness theorem for LA .
Having restricted our attention to Σ1-complete sets we are led to a stronger notion also true on countable admissible sets, namely what we shall call uniform Σ1-completeness. We will see that this notion can be viewed as extending to uncountable admissible sets, properties related to both the “recursion theory” and “proof theory” of countable admissible sets.
By following Barwise's recent approach to admissible sets allowing “urelements,” we show that there is a natural connection between certain structures 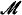 arising from the theory of inductive definability, and uniformly Σ1-complete admissible sets
arising from the theory of inductive definability, and uniformly Σ1-complete admissible sets 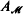 . The structures we have in mind are called uniform Kleene structures.
. The structures we have in mind are called uniform Kleene structures.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1976
Footnotes
The research for this paper was done while the author was a visitor of the University of Wisconsin, Madison, and Oxford University, England, with financial support from the University of Oslo and the Norwegian Research Council for Science and the Humanities (NAVF). The author is greatly indebted to K. J. Barwise for his encouragement and interest during the preparation of this paper.
References
REFERENCES
- 2
- Cited by


