By a classifiable theory we shall mean a theory which is superstable, without the dimensional order property, which has prime models over pairs. In order to define what we mean by unique decomposition, we remind the reader of several definitions and results. We adopt the usual conventions of stability theory and work inside a large saturated model of a fixed classifiable theory T; for instance, if we write M ⊆ N for models of T, M and N we are thinking of these models as elementary submodels of this fixed saturated models; so, in particular, M is an elementary submodel of N. Although the results will not depend on it, we will assume that T is countable to ease notation.

We do adopt one piece of notation which is not completely standard: if T is classifiable, M0 ⊆ Mi for i = 1, 2 are models of T and M1 is independent from M2 over M0 then we write M1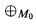M2 for the prime model over M1 ∪ M2.