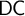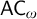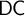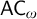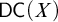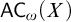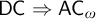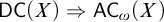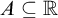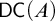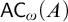1 Introduction
The axiom of choice (
![]() $\mathsf {AC}$
) is the statement
$\mathsf {AC}$
) is the statement
![]() $\forall {X} \, \mathsf {AC} ( X )$
, where
$\forall {X} \, \mathsf {AC} ( X )$
, where
The function f is a choice function for X. Observe that
![]() $\mathsf {AC} ( X )$
if and only if “X can be well-ordered”.
$\mathsf {AC} ( X )$
if and only if “X can be well-ordered”.
By restricting the choice function we have that
![]() $\mathsf {AC} ( X ) \Rightarrow \mathsf {AC}_I ( X )$
, where
$\mathsf {AC} ( X ) \Rightarrow \mathsf {AC}_I ( X )$
, where
 $$\begin{align} &\text{For any sequence }( A_i )_{ i \in I}\text{ of nonempty subsets of }X\text{ there is }\nonumber\\ &( a_i )_{ i \in I}\text{ such that }\forall { i \in I } \, ( a_i \in A_i ). \end{align}$$
$$\begin{align} &\text{For any sequence }( A_i )_{ i \in I}\text{ of nonempty subsets of }X\text{ there is }\nonumber\\ &( a_i )_{ i \in I}\text{ such that }\forall { i \in I } \, ( a_i \in A_i ). \end{align}$$
Of particular interest is the case when
![]() $I = \omega $
: the axiom of countable choice (
$I = \omega $
: the axiom of countable choice (
![]() ${\mathsf {AC}}_\omega $
) is
${\mathsf {AC}}_\omega $
) is
![]() $\forall {X} \, {\mathsf {AC}}_\omega ( X )$
. (In the literature
$\forall {X} \, {\mathsf {AC}}_\omega ( X )$
. (In the literature
![]() $\mathsf {CC}$
is another name for this axiom.)
$\mathsf {CC}$
is another name for this axiom.)
Let R be a binary relation on a set X.
-
• An R-chain is a sequence
 $( x_n )_{ n \in \omega }$
of elements of X such that
$( x_n )_{ n \in \omega }$
of elements of X such that
 $x_i \mathrel {R} x_{ i + 1}$
for all
$x_i \mathrel {R} x_{ i + 1}$
for all
 $i \in \omega $
. The element
$i \in \omega $
. The element
 $x_0$
is the starting point of the chain.
$x_0$
is the starting point of the chain. -
• An R-cycle is a finite string
 $x_0 , \dots , x_n$
of elements of X such that
$x_0 , \dots , x_n$
of elements of X such that
 $x_i \mathrel {R} x_{ i + 1}$
for all
$x_i \mathrel {R} x_{ i + 1}$
for all
 $i < n$
and
$i < n$
and
 $x_n \mathrel {R} x_0$
.
$x_n \mathrel {R} x_0$
. -
• R is total on X if
 $\forall {x \in X } \, \exists {y \in X} \, x \mathrel {R} y$
.
$\forall {x \in X } \, \exists {y \in X} \, x \mathrel {R} y$
.
Any R-cycle yields an R-chain.
The axiom of dependent choice (
![]() $\mathsf {DC}$
) is
$\mathsf {DC}$
) is
![]() $\forall {X} \, \mathsf {DC} ( X )$
, where
$\forall {X} \, \mathsf {DC} ( X )$
, where
The axioms
![]() $\mathsf {DC}$
and
$\mathsf {DC}$
and
![]() ${\mathsf {AC}}_\omega $
are ubiquitous in set theory and figure prominently in many areas of mathematics, including analysis and topology. They are probably the most popular weak forms of the axiom of choice, since they are powerful enough to enable standard mathematical constructions, yet they are weak enough to avoid the pathologies given by
${\mathsf {AC}}_\omega $
are ubiquitous in set theory and figure prominently in many areas of mathematics, including analysis and topology. They are probably the most popular weak forms of the axiom of choice, since they are powerful enough to enable standard mathematical constructions, yet they are weak enough to avoid the pathologies given by
![]() $\mathsf {AC}$
.
$\mathsf {AC}$
.
It is well-known that
![]() $\mathsf {DC} \Rightarrow {\mathsf {AC}}_\omega $
(Theorem 2.4), so one may ask if this result holds uniformly, that is: does
$\mathsf {DC} \Rightarrow {\mathsf {AC}}_\omega $
(Theorem 2.4), so one may ask if this result holds uniformly, that is: does
![]() $\mathsf {DC} ( X ) \Rightarrow {\mathsf {AC}}_\omega ( X )$
for all X? This implication holds for many Xs, but in order to prove it in general,
$\mathsf {DC} ( X ) \Rightarrow {\mathsf {AC}}_\omega ( X )$
for all X? This implication holds for many Xs, but in order to prove it in general,
![]() ${\mathsf {AC}}_\omega ( \mathbb {R} )$
must be assumed (Theorem 2.8). In Section 4, we will show that the assumption
${\mathsf {AC}}_\omega ( \mathbb {R} )$
must be assumed (Theorem 2.8). In Section 4, we will show that the assumption
![]() ${\mathsf {AC}}_\omega ( \mathbb {R} )$
cannot be dropped, as it is consistent with
${\mathsf {AC}}_\omega ( \mathbb {R} )$
cannot be dropped, as it is consistent with
![]() $\mathsf {ZF}$
that there is a set
$\mathsf {ZF}$
that there is a set
![]() $A \subseteq \mathbb {R}$
for which
$A \subseteq \mathbb {R}$
for which
![]() $ \mathsf {DC} ( A )$
holds, but
$ \mathsf {DC} ( A )$
holds, but
![]() ${\mathsf {AC}}_\omega ( A )$
fails (Theorem 4.1). In Section 5, we discuss some complementary results along with the question on the definability of the set constructed in Section 4.
${\mathsf {AC}}_\omega ( A )$
fails (Theorem 4.1). In Section 5, we discuss some complementary results along with the question on the definability of the set constructed in Section 4.
1.1 Notation
Our notation is standard(see, e.g., [Reference Jech3]). We write
![]() $X \precsim Y$
to say that there is an injection from X into Y, and
$X \precsim Y$
to say that there is an injection from X into Y, and
![]() $X \approx Y$
to say that X and Y are in bijection. Ordered pairs are denoted by
$X \approx Y$
to say that X and Y are in bijection. Ordered pairs are denoted by
![]() $( a , b )$
, finite sequences are denoted by
$( a , b )$
, finite sequences are denoted by
![]() $\mathopen \langle a_0 , \dots , a_n \mathclose \rangle $
or by
$\mathopen \langle a_0 , \dots , a_n \mathclose \rangle $
or by
![]() $( a_0 , \dots , a_n )$
, countable sequences are denoted by
$( a_0 , \dots , a_n )$
, countable sequences are denoted by
![]() $\mathopen \langle a_n \boldsymbol \mid n \in \omega \mathclose \rangle $
or by
$\mathopen \langle a_n \boldsymbol \mid n \in \omega \mathclose \rangle $
or by
![]() $( a_n )_{ n \in \omega }$
. The concatenation of a finite sequence s with a finite/countable sequence t is the finite/countable sequence
$( a_n )_{ n \in \omega }$
. The concatenation of a finite sequence s with a finite/countable sequence t is the finite/countable sequence
![]() $s {}^\smallfrown t$
obtained by listing all elements of s and then all elements of t. The set of all finite (countable) sequences from X is
$s {}^\smallfrown t$
obtained by listing all elements of s and then all elements of t. The set of all finite (countable) sequences from X is
![]() ${}^{< \omega } X$
(respectively:
${}^{< \omega } X$
(respectively:
![]() ${}^ \omega X$
). The collection of all finite subsets of a set X is
${}^ \omega X$
). The collection of all finite subsets of a set X is
![]() $[ X ]^{< \omega }$
.
$[ X ]^{< \omega }$
.
If Y is a subset of a topological space X, then
![]() $\operatorname {\mathrm {Cl}} ( Y )$
is its closure, and
$\operatorname {\mathrm {Cl}} ( Y )$
is its closure, and
![]() $\operatorname {\mathrm {Cl}}_A ( Y ) \mathrel {{:}{=}} \operatorname {\mathrm {Cl}} ( Y ) \cap A$
is the closure of
$\operatorname {\mathrm {Cl}}_A ( Y ) \mathrel {{:}{=}} \operatorname {\mathrm {Cl}} ( Y ) \cap A$
is the closure of
![]() $Y \cap A$
with respect to
$Y \cap A$
with respect to
![]() $A \subseteq X$
.
$A \subseteq X$
.
Following set-theoretic practice, we refer to members of
![]() ${}^\omega \omega $
or
${}^\omega \omega $
or
![]() $\mathscr {P} ( \omega )$
as “reals”, and we identify
$\mathscr {P} ( \omega )$
as “reals”, and we identify
![]() $\mathbb {R}$
with the Baire space
$\mathbb {R}$
with the Baire space
![]() ${}^{\omega } \omega $
or with the Cantor space
${}^{\omega } \omega $
or with the Cantor space
![]() $ {}^ \omega 2$
, depending on what is most convenient for the argument at hand.
$ {}^ \omega 2$
, depending on what is most convenient for the argument at hand.
2 Basic constructions
For the reader’s convenience, let us recall a few notions and results that will be used throughout the paper.
A set X is finite if
![]() $X \approx n$
for some
$X \approx n$
for some
![]() $n \in \omega $
; otherwise it is infinite. A set X is Dedekind-infinite if
$n \in \omega $
; otherwise it is infinite. A set X is Dedekind-infinite if
![]() $\omega \precsim X$
; otherwise it is Dedekind-finite or simply D-finite. Every finite set is D-finite, and assuming
$\omega \precsim X$
; otherwise it is Dedekind-finite or simply D-finite. Every finite set is D-finite, and assuming
![]() ${\mathsf {AC}}_\omega $
the converse holds.
${\mathsf {AC}}_\omega $
the converse holds.
It is consistent with
![]() $\mathsf {ZF}$
that infinite D-finite sets exist (see Section 3.1). By [Reference Karagila6], it is even consistent that every set is the surjective image of a D-finite set.
$\mathsf {ZF}$
that infinite D-finite sets exist (see Section 3.1). By [Reference Karagila6], it is even consistent that every set is the surjective image of a D-finite set.
Let R be a binary relation. With abuse of notation, we write
for the set of all ys that are related to x, and
for the restriction of R to the set A. The transitive closure of R
is the smallest transitive relation containing R.
The next few results are folklore.
Proposition 2.1. Let X be a set.
-
(a) If Y is the surjective image of X, then
 $\mathsf {DC} ( X ) \Rightarrow \mathsf {DC} ( Y )$
.
$\mathsf {DC} ( X ) \Rightarrow \mathsf {DC} ( Y )$
. -
(b)
 $\mathsf {DC} ( X )$
is equivalent to the seemingly stronger statement
$\mathsf {DC} ( X )$
is equivalent to the seemingly stronger statement
 $:$
For any total
$:$
For any total
 ${R \subseteq X \times X}$
and for any
${R \subseteq X \times X}$
and for any
 $a \in X$
, there is an R-chain starting from a.
$a \in X$
, there is an R-chain starting from a. -
(c) If
 $\emptyset \neq A_n \subseteq X$
and
$\emptyset \neq A_n \subseteq X$
and
 $A_n \cap A_m = \emptyset $
, then
$A_n \cap A_m = \emptyset $
, then
 $\mathsf {DC} ( X )$
implies that there is a choice function for the
$\mathsf {DC} ( X )$
implies that there is a choice function for the
 $A_n$
’s.
$A_n$
’s. -
(d)
 $\mathsf {DC} ( X \times \omega ) \Rightarrow {\mathsf {AC}}_\omega ( X )$
.
$\mathsf {DC} ( X \times \omega ) \Rightarrow {\mathsf {AC}}_\omega ( X )$
.
Proof (a) Assume
![]() $\mathsf {DC} ( X )$
and let R be a total relation on Y and let
$\mathsf {DC} ( X )$
and let R be a total relation on Y and let
![]() $F \colon X \to Y$
be a surjection. The relation
$F \colon X \to Y$
be a surjection. The relation
![]() $S = \mathopen \{{ ( x , x' ) \in X^2 }\boldsymbol \mid { ( F ( x ) , F ( x ' ) ) \in R } \mathclose \}$
is total on X, so by assumption there is an S-chain
$S = \mathopen \{{ ( x , x' ) \in X^2 }\boldsymbol \mid { ( F ( x ) , F ( x ' ) ) \in R } \mathclose \}$
is total on X, so by assumption there is an S-chain
![]() $( x_n )_{ n \in \omega }$
. Then
$( x_n )_{ n \in \omega }$
. Then
![]() $( F ( x_n ) )_{ n \in \omega }$
is an R-chain.
$( F ( x_n ) )_{ n \in \omega }$
is an R-chain.
(b) Suppose
![]() $R \subseteq X^2$
is total and let
$R \subseteq X^2$
is total and let
![]() $a \in X$
. Observe that
$a \in X$
. Observe that
![]() $S = R {\mathop {\upharpoonright }} R^+ ( a )$
is total on
$S = R {\mathop {\upharpoonright }} R^+ ( a )$
is total on
![]() $R^+ ( a )$
. By part (a)
$R^+ ( a )$
. By part (a)
![]() $\mathsf {DC} ( R^+ ( a ) )$
holds, hence there is an S-chain
$\mathsf {DC} ( R^+ ( a ) )$
holds, hence there is an S-chain
![]() $( y_n )_{ n \in \omega }$
. Let
$( y_n )_{ n \in \omega }$
. Let
![]() $( x_0 , \dots , x_{ k + 1} )$
witness that
$( x_0 , \dots , x_{ k + 1} )$
witness that
![]() $y_0 \in R^+ ( a )$
, i.e.,
$y_0 \in R^+ ( a )$
, i.e.,
![]() $x_0 = a$
,
$x_0 = a$
,
![]() $x_{k+1} = y_0$
and
$x_{k+1} = y_0$
and
![]() $x_i \mathrel {R} x_{i+1}$
for all
$x_i \mathrel {R} x_{i+1}$
for all
![]() $i \le k$
: then
$i \le k$
: then
![]() $( x_0 , \dots , x_k ) {}^\smallfrown ( y_n )_{ n \in \omega }$
is an R-chain starting from a.
$( x_0 , \dots , x_k ) {}^\smallfrown ( y_n )_{ n \in \omega }$
is an R-chain starting from a.
(c) Let R be the relation on
![]() $\bigcup _n A_n \subseteq X$
defined by
$\bigcup _n A_n \subseteq X$
defined by
By part (a)
![]() $\mathsf {DC} ( \bigcup _n A_n )$
holds, hence by part (b) there is an R-chain
$\mathsf {DC} ( \bigcup _n A_n )$
holds, hence by part (b) there is an R-chain
![]() $( a_n )_{ n \in \omega }$
in
$( a_n )_{ n \in \omega }$
in
![]() $\bigcup _n A_n$
starting from any
$\bigcup _n A_n$
starting from any
![]() $a_0 \in A_0$
. Observe that any R-chain
$a_0 \in A_0$
. Observe that any R-chain
![]() $( a_n )_{n \in \omega }$
with
$( a_n )_{n \in \omega }$
with
![]() $a_0 \in A_0$
is such that
$a_0 \in A_0$
is such that
![]() $a_n \in A_n$
for all
$a_n \in A_n$
for all
![]() $n \in \omega $
.
$n \in \omega $
.
(d) Given
![]() $\emptyset \neq A_n \subseteq X$
, let
$\emptyset \neq A_n \subseteq X$
, let
![]() $\bar {A}_n = A_n \times \mathopen \{ {n} \mathclose \} \subseteq X \times \omega $
. By hypothesis and part (c), there is a sequence
$\bar {A}_n = A_n \times \mathopen \{ {n} \mathclose \} \subseteq X \times \omega $
. By hypothesis and part (c), there is a sequence
![]() $( a_n , n)_{n \in \omega }$
such that
$( a_n , n)_{n \in \omega }$
such that
![]() $(a_n , n ) \in \bar {A}_n$
, hence
$(a_n , n ) \in \bar {A}_n$
, hence
![]() $a_n \in A_n$
.
$a_n \in A_n$
.
The gist of part (c) of Proposition 2.1 is that we can use dependent choice rather than countable choice whenever the sets we choose from are disjoint. Here is an example of such an application.
Lemma 2.2. Suppose X is a first countable
![]() $\mathrm {T}_1$
space and
$\mathrm {T}_1$
space and
![]() $a \in \operatorname {\mathrm {Cl}} ( A ) \setminus A$
where
$a \in \operatorname {\mathrm {Cl}} ( A ) \setminus A$
where
![]() $A \subseteq X$
. Assume
$A \subseteq X$
. Assume
![]() $\mathsf {DC} ( A )$
holds. Then there are distinct
$\mathsf {DC} ( A )$
holds. Then there are distinct
![]() $a_n \in A$
such that
$a_n \in A$
such that
![]() $a_n \to a$
. In particular
$a_n \to a$
. In particular
![]() $\omega \precsim A$
.
$\omega \precsim A$
.
Proof Let
![]() $\mathopen \{{ U_n }\boldsymbol \mid { n \in \omega } \mathclose \}$
be a neighborhood base for a, with
$\mathopen \{{ U_n }\boldsymbol \mid { n \in \omega } \mathclose \}$
be a neighborhood base for a, with
![]() $U_{n+1}\subseteq U_n$
for every n. Given that X is
$U_{n+1}\subseteq U_n$
for every n. Given that X is
![]() $\mathrm {T}_1$
, we can assume, by passing to a subsequence if needed, that
$\mathrm {T}_1$
, we can assume, by passing to a subsequence if needed, that
![]() $A_n = ( U_n \setminus U_{ n + 1 } ) \cap A$
is nonempty for every n. Since the
$A_n = ( U_n \setminus U_{ n + 1 } ) \cap A$
is nonempty for every n. Since the
![]() $A_n$
s are pairwise disjoint and nonempty, by Proposition 2.1(c) there is a sequence of
$A_n$
s are pairwise disjoint and nonempty, by Proposition 2.1(c) there is a sequence of
![]() $( a_n ) _{ n \in \omega }$
of distinct elements of A such that
$( a_n ) _{ n \in \omega }$
of distinct elements of A such that
![]() $a_n \in A_n$
for every n.
$a_n \in A_n$
for every n.
Lemma 2.3. Let X be a set.
-
(a)
 $X \times 2 \precsim X \Rightarrow X \times \omega \precsim X$
.
$X \times 2 \precsim X \Rightarrow X \times \omega \precsim X$
. -
(b) If
 $X \neq \emptyset $
, then
$X \neq \emptyset $
, then
 ${}^{< \omega } ( {}^{< \omega } X ) \precsim {}^{< \omega } X$
, so
${}^{< \omega } ( {}^{< \omega } X ) \precsim {}^{< \omega } X$
, so
 ${}^{< \omega } X \times 2 \precsim {}^{< \omega } X$
.
${}^{< \omega } X \times 2 \precsim {}^{< \omega } X$
. -
(c)
 $\forall {X} \, \exists {Y} \, ( X \subseteq Y \wedge {}^{< \omega } Y \precsim Y )$
.
$\forall {X} \, \exists {Y} \, ( X \subseteq Y \wedge {}^{< \omega } Y \precsim Y )$
.
Proof (a) If
![]() $f_0 , f_1 \colon X \to X$
are injections with
$f_0 , f_1 \colon X \to X$
are injections with
![]() $\operatorname {\mathrm {ran}} ( f_0 ) \cap \operatorname {\mathrm {ran}} ( f_1 ) = \emptyset $
, then define an injection
$\operatorname {\mathrm {ran}} ( f_0 ) \cap \operatorname {\mathrm {ran}} ( f_1 ) = \emptyset $
, then define an injection
![]() $F \colon X \times \omega \to X$
as follows:
$F \colon X \times \omega \to X$
as follows:
 $$\begin{align*}F ( x , 0 ) = f_0 ( x ), \qquad F ( x , n + 1 ) = \underbrace{f_1\circ \dots \circ f_1}_{n+1 \text{ times}} \circ f_0 ( x ). \end{align*}$$
$$\begin{align*}F ( x , 0 ) = f_0 ( x ), \qquad F ( x , n + 1 ) = \underbrace{f_1\circ \dots \circ f_1}_{n+1 \text{ times}} \circ f_0 ( x ). \end{align*}$$
(b) If X is a singleton, then
![]() ${}^{< \omega } X \approx \omega $
, and the result follows at once. If X has at least two elements, the result follows from [Reference Andretta and Ros1, Proposition 2.1].
${}^{< \omega } X \approx \omega $
, and the result follows at once. If X has at least two elements, the result follows from [Reference Andretta and Ros1, Proposition 2.1].
(c) Given X take
![]() $Y = \mathord {\mathrm {V}}_ \lambda $
with sufficiently large limit
$Y = \mathord {\mathrm {V}}_ \lambda $
with sufficiently large limit
![]() $\lambda $
.
$\lambda $
.
From Lemma 2.3 and Proposition 2.1(d) we obtain at once:
Theorem 2.4.
-
(a) If
 $X \times 2 \precsim X$
, then
$X \times 2 \precsim X$
, then
 $\mathsf {DC} ( X ) \Rightarrow {\mathsf {AC}}_\omega ( X )$
. In particular
$\mathsf {DC} ( X ) \Rightarrow {\mathsf {AC}}_\omega ( X )$
. In particular
 $: \mathsf {DC} ( \mathbb {R} ) \Rightarrow {\mathsf {AC}}_\omega ( \mathbb {R} )$
.
$: \mathsf {DC} ( \mathbb {R} ) \Rightarrow {\mathsf {AC}}_\omega ( \mathbb {R} )$
. -
(b)
 $\forall {X} \, \exists {Y} \, ( X \subseteq Y \wedge ( \mathsf {DC} ( Y ) \Rightarrow {\mathsf {AC}}_\omega ( Y ) )$
.
$\forall {X} \, \exists {Y} \, ( X \subseteq Y \wedge ( \mathsf {DC} ( Y ) \Rightarrow {\mathsf {AC}}_\omega ( Y ) )$
. -
(c)
 $\mathsf {DC} \Rightarrow {\mathsf {AC}}_\omega $
.
$\mathsf {DC} \Rightarrow {\mathsf {AC}}_\omega $
.
Lemma 2.5.
-
(a) Let
 $A \subseteq \mathbb {R}$
. Then
$A \subseteq \mathbb {R}$
. Then
 ${\mathsf {AC}}_\omega ( A ) \Rightarrow A$
is separable.
${\mathsf {AC}}_\omega ( A ) \Rightarrow A$
is separable. -
(b)
 ${\mathsf {AC}}_\omega ( \mathbb {R} ) \Leftrightarrow \forall {A \subseteq \mathbb {R}} \, ( A \text { is separable} )$
.
${\mathsf {AC}}_\omega ( \mathbb {R} ) \Leftrightarrow \forall {A \subseteq \mathbb {R}} \, ( A \text { is separable} )$
. -
(c) Suppose
 $A \subseteq \mathbb {R}$
contains a nonempty perfect set, and assume
$A \subseteq \mathbb {R}$
contains a nonempty perfect set, and assume
 $\mathsf {DC} ( A )$
. Then
$\mathsf {DC} ( A )$
. Then
 $\mathsf {DC} ( \mathbb {R} )$
holds, and hence
$\mathsf {DC} ( \mathbb {R} )$
holds, and hence
 ${\mathsf {AC}}_\omega ( A )$
holds.
${\mathsf {AC}}_\omega ( A )$
holds.
Proof As A is second countable, part (a) of Lemma 2.5 follows.
(b) The direction
![]() $( \Rightarrow )$
is a direct consequence of part (a). For the other direction, fix a sequence
$( \Rightarrow )$
is a direct consequence of part (a). For the other direction, fix a sequence
![]() $( A_n )_{ n \in \omega }$
of nonempty subsets of
$( A_n )_{ n \in \omega }$
of nonempty subsets of
![]() ${}^ \omega \omega $
and consider the set
${}^ \omega \omega $
and consider the set
![]() $A = \mathopen \{{ \mathopen \langle n \mathclose \rangle {}^\smallfrown x }\boldsymbol \mid { n \in \omega \text { and } x \in A_n } \mathclose \}$
. From an enumeration of a dense subset of A (which exists by assumption), we can extract a choice function for
$A = \mathopen \{{ \mathopen \langle n \mathclose \rangle {}^\smallfrown x }\boldsymbol \mid { n \in \omega \text { and } x \in A_n } \mathclose \}$
. From an enumeration of a dense subset of A (which exists by assumption), we can extract a choice function for
![]() $( A_n )_{ n \in \omega }$
.
$( A_n )_{ n \in \omega }$
.
(c) If
![]() $P \subseteq A$
is perfect, then
$P \subseteq A$
is perfect, then
![]() $P \approx \mathbb {R}$
, and since A surjects onto P, then
$P \approx \mathbb {R}$
, and since A surjects onto P, then
![]() $\mathsf {DC} ( \mathbb {R} )$
holds, and hence
$\mathsf {DC} ( \mathbb {R} )$
holds, and hence
![]() ${\mathsf {AC}}_\omega ( \mathbb {R} )$
holds.
${\mathsf {AC}}_\omega ( \mathbb {R} )$
holds.
Note that the implication in part (a) of Lemma 2.5 cannot be reversed: if
![]() $A \subseteq \mathbb {R}$
is a witness of the failure of countable choice, then the same is true of the separable set
$A \subseteq \mathbb {R}$
is a witness of the failure of countable choice, then the same is true of the separable set
![]() $A \cup \mathbb {Q}$
.
$A \cup \mathbb {Q}$
.
2.1
 ${\mathsf {AC}}_\omega ( X )$
follows from
${\mathsf {AC}}_\omega ( X )$
follows from
 $\mathsf {DC} ( X )$
together with
$\mathsf {DC} ( X )$
together with
 ${\mathsf {AC}}_\omega ( \mathbb {R} )$
${\mathsf {AC}}_\omega ( \mathbb {R} )$
Let us start with the following combinatorial result that might be of independent interest. It is stated for families of sets indexed by an arbitrary set I, but when
![]() $I = \omega $
the assumption
$I = \omega $
the assumption
![]() $\mathsf {AC}_I ( \mathscr {P} ( I ) )$
becomes
$\mathsf {AC}_I ( \mathscr {P} ( I ) )$
becomes
![]() ${\mathsf {AC}}_\omega ( \mathbb {R} )$
.
${\mathsf {AC}}_\omega ( \mathbb {R} )$
.
Lemma 2.6. Let
![]() $( X_i )_{ i \in I }$
be nonempty sets, and assume
$( X_i )_{ i \in I }$
be nonempty sets, and assume
![]() $\mathsf {AC}_I ( \mathscr {P} ( I ) )$
. Then there are
$\mathsf {AC}_I ( \mathscr {P} ( I ) )$
. Then there are
![]() $( Y_i )_{ i \in I }$
such that
$( Y_i )_{ i \in I }$
such that
![]() $\emptyset \neq Y_i \subseteq X_i$
and for all
$\emptyset \neq Y_i \subseteq X_i$
and for all
![]() $i , j \in I$
either
$i , j \in I$
either
![]() $Y_i = Y_j$
or else
$Y_i = Y_j$
or else
![]() $Y_i \cap Y_j = \emptyset $
.
$Y_i \cap Y_j = \emptyset $
.
Proof Let
![]() $F \colon \bigcup _{i \in I} X_i \to \mathscr {P} ( I )$
,
$F \colon \bigcup _{i \in I} X_i \to \mathscr {P} ( I )$
,
![]() $F ( x ) = \mathopen \{{ i \in I }\boldsymbol \mid { x \in X_i } \mathclose \}$
and let
$F ( x ) = \mathopen \{{ i \in I }\boldsymbol \mid { x \in X_i } \mathclose \}$
and let
![]() $A_i = \mathopen \{{ a \in \operatorname {\mathrm {ran}} ( F ) }\boldsymbol \mid { i \in a } \mathclose \}$
. Observe that for all
$A_i = \mathopen \{{ a \in \operatorname {\mathrm {ran}} ( F ) }\boldsymbol \mid { i \in a } \mathclose \}$
. Observe that for all
![]() $x \in \bigcup _{i \in I} X_i$
and all
$x \in \bigcup _{i \in I} X_i$
and all
![]() $i \in I$
$i \in I$
In particular,
![]() $\emptyset \neq A_i \subseteq \mathscr {P} ( I )$
for all
$\emptyset \neq A_i \subseteq \mathscr {P} ( I )$
for all
![]() $i \in I$
. By
$i \in I$
. By
![]() $\mathsf {AC}_I ( \mathscr {P} ( I ) )$
pick
$\mathsf {AC}_I ( \mathscr {P} ( I ) )$
pick
![]() $a_i \in A_i$
, and let
$a_i \in A_i$
, and let
![]() $Y_i = F^{-1} ( \mathopen \{ {a_i} \mathclose \} ) \subseteq \bigcup _{i \in I} X_i$
. Then
$Y_i = F^{-1} ( \mathopen \{ {a_i} \mathclose \} ) \subseteq \bigcup _{i \in I} X_i$
. Then
and since
![]() $i \in a_i$
, then
$i \in a_i$
, then
![]() $Y_i \subseteq X_i$
. The sets
$Y_i \subseteq X_i$
. The sets
![]() $Y_i$
need not be distinct as the
$Y_i$
need not be distinct as the
![]() $a_i$
s need not be distinct, but if
$a_i$
s need not be distinct, but if
![]() $a_i \neq a_ j$
, then
$a_i \neq a_ j$
, then
![]() $Y_i \cap Y_j = \emptyset $
.
$Y_i \cap Y_j = \emptyset $
.
By (1) if the
![]() $X_i$
s are finite, then so are the
$X_i$
s are finite, then so are the
![]() $A_i$
s. If, moreover,
$A_i$
s. If, moreover,
![]() $\mathscr {P} ( I )$
is linearly orderable (e.g., when I is well-orderable), then the
$\mathscr {P} ( I )$
is linearly orderable (e.g., when I is well-orderable), then the
![]() $a_i$
s can be chosen without appealing to any choice axiom. Therefore:
$a_i$
s can be chosen without appealing to any choice axiom. Therefore:
Corollary 2.7. If
![]() $\mathscr {P} ( I )$
is linearly orderable and
$\mathscr {P} ( I )$
is linearly orderable and
![]() $( X_i )_{ i \in I }$
are finite, nonempty sets, then there are
$( X_i )_{ i \in I }$
are finite, nonempty sets, then there are
![]() $\emptyset \neq Y_i \subseteq X_i$
such that for all
$\emptyset \neq Y_i \subseteq X_i$
such that for all
![]() $i , j \in I$
either
$i , j \in I$
either
![]() $Y_i = Y_j$
or else
$Y_i = Y_j$
or else
![]() $Y_i \cap Y_j = \emptyset $
.
$Y_i \cap Y_j = \emptyset $
.
Theorem 2.8. Assume
![]() ${\mathsf {AC}}_\omega ( \mathbb {R} )$
, then
${\mathsf {AC}}_\omega ( \mathbb {R} )$
, then
![]() $\forall {X} \, ( \mathsf {DC} ( X ) \Rightarrow {\mathsf {AC}}_\omega ( X ) )$
.
$\forall {X} \, ( \mathsf {DC} ( X ) \Rightarrow {\mathsf {AC}}_\omega ( X ) )$
.
Proof Assume
![]() $\mathsf {DC} ( X )$
and let
$\mathsf {DC} ( X )$
and let
![]() $\emptyset \neq X_n \subseteq X$
for
$\emptyset \neq X_n \subseteq X$
for
![]() $n \in \omega $
. By Lemma 2.6, there are
$n \in \omega $
. By Lemma 2.6, there are
![]() $\emptyset \neq Y_n \subseteq X_n$
such that for all
$\emptyset \neq Y_n \subseteq X_n$
such that for all
![]() $n , m \in \omega $
either
$n , m \in \omega $
either
![]() $Y_n = Y_m$
or else
$Y_n = Y_m$
or else
![]() $Y_n \cap Y_m = \emptyset $
. Let
$Y_n \cap Y_m = \emptyset $
. Let
![]() $I \subseteq \omega $
be such that
$I \subseteq \omega $
be such that
![]() $\mathopen \{{ Y_i }\boldsymbol \mid { i \in I } \mathclose \} = \mathopen \{{ Y_n }\boldsymbol \mid { n \in \omega } \mathclose \}$
and
$\mathopen \{{ Y_i }\boldsymbol \mid { i \in I } \mathclose \} = \mathopen \{{ Y_n }\boldsymbol \mid { n \in \omega } \mathclose \}$
and
![]() $Y_i \cap Y_j = \emptyset $
for every distinct
$Y_i \cap Y_j = \emptyset $
for every distinct
![]() $ i , j \in I$
. If we can find
$ i , j \in I$
. If we can find
![]() $y_i \in Y_i$
for all
$y_i \in Y_i$
for all
![]() $i \in I$
, then we can extend this to a choice sequence
$i \in I$
, then we can extend this to a choice sequence
![]() $y_n \in Y_n \subseteq X_n$
for all
$y_n \in Y_n \subseteq X_n$
for all
![]() $n \in \omega $
as required. If I is finite, then the
$n \in \omega $
as required. If I is finite, then the
![]() $y_i$
s can be found without any appeal to choice. If I is infinite, then
$y_i$
s can be found without any appeal to choice. If I is infinite, then
![]() $I \approx \omega $
so we can find the
$I \approx \omega $
so we can find the
![]() $y_i$
s by Proposition 2.1(c).
$y_i$
s by Proposition 2.1(c).
The following result follows from the argument of Theorem 2.8 together with Corollary 2.7.
Corollary 2.9.
![]() $\forall {X} \, ( \mathsf {DC} ( X ) \Rightarrow {\mathsf {AC}}_\omega ^{< \omega } ( X ))$
, where
$\forall {X} \, ( \mathsf {DC} ( X ) \Rightarrow {\mathsf {AC}}_\omega ^{< \omega } ( X ))$
, where
![]() ${\mathsf {AC}}_\omega ^{< \omega } ( X )$
asserts that every countable collection of nonempty finite subsets of X has a choice function.
${\mathsf {AC}}_\omega ^{< \omega } ( X )$
asserts that every countable collection of nonempty finite subsets of X has a choice function.
2.2 Does
 $\mathsf {DC} ( X )$
imply
$\mathsf {DC} ( X )$
imply
 ${\mathsf {AC}}_\omega ( X )$
?
${\mathsf {AC}}_\omega ( X )$
?
follows from either one of the following assumptions:
-
•
 $X \times 2 \precsim X$
for all infinite X,
$X \times 2 \precsim X$
for all infinite X, -
•
 ${\mathsf {AC}}_\omega ( \mathbb {R} )$
.
${\mathsf {AC}}_\omega ( \mathbb {R} )$
.
Sageev in [Reference Sageev10] proved that “
![]() $X \times 2 \precsim X$
for all infinite X” does not imply
$X \times 2 \precsim X$
for all infinite X” does not imply
![]() ${\mathsf {AC}}_\omega ( \mathbb {R} )$
, while Monro in [Reference Monro9] proved that
${\mathsf {AC}}_\omega ( \mathbb {R} )$
, while Monro in [Reference Monro9] proved that
![]() $\mathsf {DC}$
(and hence the weaker
$\mathsf {DC}$
(and hence the weaker
![]() ${\mathsf {AC}}_\omega ( \mathbb {R} )$
) does not imply “
${\mathsf {AC}}_\omega ( \mathbb {R} )$
) does not imply “
![]() $X \times 2 \precsim X$
for all infinite X”. So neither assumption implies the other.
$X \times 2 \precsim X$
for all infinite X”. So neither assumption implies the other.
The obvious question is if (2) is a theorem of
![]() $\mathsf {ZF}$
. Suppose that there is a set X such that
$\mathsf {ZF}$
. Suppose that there is a set X such that
![]() $\mathsf {DC} ( X ) \wedge \neg {\mathsf {AC}}_\omega ( X )$
. By the proof of Lemma 2.6 the set
$\mathsf {DC} ( X ) \wedge \neg {\mathsf {AC}}_\omega ( X )$
. By the proof of Lemma 2.6 the set
![]() $A \mathrel {{:}{=}} F [ X ] \subseteq \mathscr {P} ( \omega )$
is such that
$A \mathrel {{:}{=}} F [ X ] \subseteq \mathscr {P} ( \omega )$
is such that
![]() $\mathsf {DC} ( A )$
holds, as A is the surjective image of X, and
$\mathsf {DC} ( A )$
holds, as A is the surjective image of X, and
![]() $ {\mathsf {AC}}_\omega ( A )$
fails, as otherwise, arguing as in Theorem 2.8,
$ {\mathsf {AC}}_\omega ( A )$
fails, as otherwise, arguing as in Theorem 2.8,
![]() ${\mathsf {AC}}_\omega ( X )$
would hold. Therefore if (2) fails, then the witness of this failure can be taken to be a subset of
${\mathsf {AC}}_\omega ( X )$
would hold. Therefore if (2) fails, then the witness of this failure can be taken to be a subset of
![]() $\mathbb {R}$
. In Section 4 we construct a model of
$\mathbb {R}$
. In Section 4 we construct a model of
![]() $\mathsf {ZF}$
in which
$\mathsf {ZF}$
in which
showing that (2) is not a theorem of
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
By Lemma 2.5(c), any A as in (3) cannot contain a nonempty perfect set. Moreover, such a set A also needs to be Dedekind-infinite: indeed, A cannot be closed, as otherwise, by the usual Cantor–Bendixson argument, it would either be countable, contradicting
![]() $\neg {\mathsf {AC}}_\omega (A)$
, or else it would contain a nonempty perfect set, which we already excluded; therefore A is not closed, and, by Lemma 2.2, A is Dedekind-infinite.
$\neg {\mathsf {AC}}_\omega (A)$
, or else it would contain a nonempty perfect set, which we already excluded; therefore A is not closed, and, by Lemma 2.2, A is Dedekind-infinite.
It can be shown that (3) fails both in Cohen’s first model (Proposition 3.4) and in the Feferman–Levy model (Proposition 5.3), and hence in both these models (2) holds.
2.3 An equivalent formulation of
 $\mathsf {DC}$
$\mathsf {DC}$
A tree on X is a
![]() $T \subseteq {}^{< \omega } X$
that is closed under initial segments, that is if
$T \subseteq {}^{< \omega } X$
that is closed under initial segments, that is if
![]() $t \in T$
and
$t \in T$
and
![]() $s \subseteq t$
then
$s \subseteq t$
then
![]() $s \in T$
. A tree T on X is pruned if for every
$s \in T$
. A tree T on X is pruned if for every
![]() $t \in T$
there is
$t \in T$
there is
![]() $s \in T$
such that
$s \in T$
such that
![]() $t \subset s$
. A branch of T is a
$t \subset s$
. A branch of T is a
![]() $b \colon \omega \to X$
such that
$b \colon \omega \to X$
such that
![]() $\forall {n \in \omega } \, ( b {\mathop {\upharpoonright }} n \in T)$
. A tree T is ill-founded if it has a branch; otherwise it is well-founded. Let
$\forall {n \in \omega } \, ( b {\mathop {\upharpoonright }} n \in T)$
. A tree T is ill-founded if it has a branch; otherwise it is well-founded. Let
and let
![]() $\mathsf {DC}_ \omega $
be
$\mathsf {DC}_ \omega $
be
![]() $\forall {X} \, \mathsf {DC}_ \omega ( X )$
. As
$\forall {X} \, \mathsf {DC}_ \omega ( X )$
. As
![]() $\mathsf {DC}$
is equivalent to
$\mathsf {DC}$
is equivalent to
![]() $\mathsf {DC}_ \omega $
(Corollary 2.11), the axiom of dependent choice is often stated as
$\mathsf {DC}_ \omega $
(Corollary 2.11), the axiom of dependent choice is often stated as
![]() $\mathsf {DC}_\omega $
. The advantage of this formulation is that it can be generalized to ordinals larger than
$\mathsf {DC}_\omega $
. The advantage of this formulation is that it can be generalized to ordinals larger than
![]() $\omega $
.
$\omega $
.
Proposition 2.10.
![]() $\mathsf {DC}_\omega ( X ) \Leftrightarrow \mathsf {DC} ( {}^{< \omega } X )$
, for every nonempty set X.
$\mathsf {DC}_\omega ( X ) \Leftrightarrow \mathsf {DC} ( {}^{< \omega } X )$
, for every nonempty set X.
Proof (
![]() $\Rightarrow $
) Suppose R is a binary relation on
$\Rightarrow $
) Suppose R is a binary relation on
![]() ${}^{< \omega } X$
such that
${}^{< \omega } X$
such that
![]() $\forall {s} \, \exists {t} \, ( s \mathrel {R} t )$
. If
$\forall {s} \, \exists {t} \, ( s \mathrel {R} t )$
. If
![]() $\emptyset \mathrel {R} \emptyset $
, then
$\emptyset \mathrel {R} \emptyset $
, then
![]() $\mathopen \langle \emptyset , \emptyset , \dots \mathclose \rangle $
is an R-chain as required, so we may assume otherwise. Let
$\mathopen \langle \emptyset , \emptyset , \dots \mathclose \rangle $
is an R-chain as required, so we may assume otherwise. Let
![]() $R' \subseteq R$
be the sub-relation on
$R' \subseteq R$
be the sub-relation on
![]() ${}^{< \omega } X$
defined by
${}^{< \omega } X$
defined by
The relation
![]() $R'$
is total and any
$R'$
is total and any
![]() $R'$
-chain is an R-chain. Then
$R'$
-chain is an R-chain. Then
is a pruned tree on X, so it has a branch. By the minimality assumption of
![]() $R'$
, given a branch b of T one can construct inductively an
$R'$
, given a branch b of T one can construct inductively an
![]() $R'$
-chain
$R'$
-chain
![]() $( s_n )_{ n \in \omega }$
such that
$( s_n )_{ n \in \omega }$
such that
![]() $s_0 {}^\smallfrown s_1 {}^\smallfrown \dots {}^\smallfrown s_n \subseteq b$
for all n.
$s_0 {}^\smallfrown s_1 {}^\smallfrown \dots {}^\smallfrown s_n \subseteq b$
for all n.
(
![]() $\Leftarrow $
) If T is a pruned tree on X, let
$\Leftarrow $
) If T is a pruned tree on X, let
![]() $R \subseteq T \times T$
be defined by
$R \subseteq T \times T$
be defined by
As
![]() $T \subseteq {}^{< \omega } X$
then
$T \subseteq {}^{< \omega } X$
then
![]() $\mathsf {DC} ( T )$
holds, and since R is total, as T is pruned, there is an R-chain. Any such chain yields a branch of T.
$\mathsf {DC} ( T )$
holds, and since R is total, as T is pruned, there is an R-chain. Any such chain yields a branch of T.
Corollary 2.11.
![]() $\mathsf {DC} \Leftrightarrow \mathsf {DC}_ \omega $
.
$\mathsf {DC} \Leftrightarrow \mathsf {DC}_ \omega $
.
Proposition 2.12. Let X be a set.
-
(a)
 $\mathsf {DC}_ \omega ( X ) \Rightarrow \mathsf {DC} ( X )$
.
$\mathsf {DC}_ \omega ( X ) \Rightarrow \mathsf {DC} ( X )$
. -
(b)
 $\mathsf {DC}_ \omega ( X ) \Rightarrow {\mathsf {AC}}_\omega ( X )$
.
$\mathsf {DC}_ \omega ( X ) \Rightarrow {\mathsf {AC}}_\omega ( X )$
.
Proof
X injects into
![]() ${}^{< \omega } X$
, so part (a) holds by Proposition 2.10.
${}^{< \omega } X$
, so part (a) holds by Proposition 2.10.
For part (b) argue as follows. If
![]() $(A_n)_{ n \in \omega }$
is a sequence of nonempty subsets of X, then
$(A_n)_{ n \in \omega }$
is a sequence of nonempty subsets of X, then
![]() $\mathopen \{{ \mathopen \langle x_0 , \dots , x_{ n - 1 } \mathclose \rangle }\boldsymbol \mid { \forall {i < n} \, ( x_i \in A_i ) } \mathclose \}$
is a pruned tree on X, and any branch of it is a sequence
$\mathopen \{{ \mathopen \langle x_0 , \dots , x_{ n - 1 } \mathclose \rangle }\boldsymbol \mid { \forall {i < n} \, ( x_i \in A_i ) } \mathclose \}$
is a pruned tree on X, and any branch of it is a sequence
![]() $( a_n )_{ n \in \omega }$
such that
$( a_n )_{ n \in \omega }$
such that
![]() $a_n \in A_n$
for all
$a_n \in A_n$
for all
![]() $n \in \omega $
.
$n \in \omega $
.
In light of Proposition 2.12, our main result, Theorem 4.1, tells us it is consistent with
![]() $\mathsf {ZF}$
that there is a set
$\mathsf {ZF}$
that there is a set
![]() $A\subseteq \mathbb {R}$
for which
$A\subseteq \mathbb {R}$
for which
![]() $\mathsf {DC} (A)$
holds but
$\mathsf {DC} (A)$
holds but
![]() $ \mathsf {DC}_ \omega ( A )$
fails.
$ \mathsf {DC}_ \omega ( A )$
fails.
3 Symmetric extensions
The model we construct in Section 4 is an iterated symmetric extension. For the reader’s convenience, let us recall a few facts about forcing and symmetric extensions.
If
![]() $\mathbf { P}$
is a forcing notion, i.e., a preordered set with a maximum
$\mathbf { P}$
is a forcing notion, i.e., a preordered set with a maximum
![]() $1_{ \mathbf { P}}$
, we convene that
$1_{ \mathbf { P}}$
, we convene that
![]() $p \leq _{ \mathbf { P}} q$
means that p is stronger than q. When there is no danger of confusion, we drop the subscript
$p \leq _{ \mathbf { P}} q$
means that p is stronger than q. When there is no danger of confusion, we drop the subscript
![]() $\mathbf { P}$
. Dotted letters
$\mathbf { P}$
. Dotted letters
![]() $\dot {x}, \dot {y} , \dots $
vary over the class of
$\dot {x}, \dot {y} , \dots $
vary over the class of
![]() $\mathbf { P}$
-names,
$\mathbf { P}$
-names,
![]() $\check {x}$
is the canonical
$\check {x}$
is the canonical
![]() $\mathbf { P}$
-name for x, while
$\mathbf { P}$
-name for x, while
![]() $\dot {G}$
is the
$\dot {G}$
is the
![]() $\mathbf { P}$
-name for the generic filter. If F is a set of
$\mathbf { P}$
-name for the generic filter. If F is a set of
![]() $\mathbf { P}$
-names, then, following Karagila’s notation [Reference Karagila5],
$\mathbf { P}$
-names, then, following Karagila’s notation [Reference Karagila5],
![]() $F^\bullet $
is the
$F^\bullet $
is the
![]() $\mathbf { P}$
-name
$\mathbf { P}$
-name
![]() $\mathopen \{{ ( \dot {x} , 1 ) }\boldsymbol \mid { \dot {x} \in F } \mathclose \}$
. This notation extends naturally to ordered pairs and sequences, so
$\mathopen \{{ ( \dot {x} , 1 ) }\boldsymbol \mid { \dot {x} \in F } \mathclose \}$
. This notation extends naturally to ordered pairs and sequences, so
![]() $( \dot {x} , \dot {y} )^\bullet \mathrel {{:}{=}} \mathopen \{ { \mathopen \{ { \dot {x}} \mathclose \}^\bullet , \mathopen \{ { \dot {x},\dot {y} } \mathclose \}^\bullet } \mathclose \}^\bullet $
and so on. If
$( \dot {x} , \dot {y} )^\bullet \mathrel {{:}{=}} \mathopen \{ { \mathopen \{ { \dot {x}} \mathclose \}^\bullet , \mathopen \{ { \dot {x},\dot {y} } \mathclose \}^\bullet } \mathclose \}^\bullet $
and so on. If
![]() $G \subseteq \mathbf { P}$
is
$G \subseteq \mathbf { P}$
is
![]() $\mathord {\mathrm {V}}$
-generic, then
$\mathord {\mathrm {V}}$
-generic, then
![]() $\dot {x}_G$
is the object in
$\dot {x}_G$
is the object in
![]() $\mathord {\mathrm {V}} [ G ]$
obtained by evaluating
$\mathord {\mathrm {V}} [ G ]$
obtained by evaluating
![]() $\dot {x}$
with G.
$\dot {x}$
with G.
Let
![]() $\mathbf { P}$
be a forcing notion. Every automorphism
$\mathbf { P}$
be a forcing notion. Every automorphism
![]() $\pi \in \operatorname {\mathrm {Aut}} ( \mathbf { P} )$
acts canonically on
$\pi \in \operatorname {\mathrm {Aut}} ( \mathbf { P} )$
acts canonically on
![]() $\mathbf { P}$
-names as follows: given
$\mathbf { P}$
-names as follows: given
![]() $\dot {x}$
a
$\dot {x}$
a
![]() $\mathbf { P}$
-name,
$\mathbf { P}$
-name,
Lemma 3.1 (Symmetry Lemma, [Reference Jech3, Lemma 14.37]).
Let
![]() $\mathbf { P}$
be a forcing notion,
$\mathbf { P}$
be a forcing notion,
![]() $\pi \in \operatorname {\mathrm {Aut}} ( \mathbf { P} )$
and
$\pi \in \operatorname {\mathrm {Aut}} ( \mathbf { P} )$
and
![]() $\dot {x}_1 , \dots , \dot {x}_n$
be
$\dot {x}_1 , \dots , \dot {x}_n$
be
![]() $\mathbf { P}$
-names. For every formula
$\mathbf { P}$
-names. For every formula ![]()
Let
![]() $\mathcal {G}$
be a subgroup of
$\mathcal {G}$
be a subgroup of
![]() $\operatorname {\mathrm {Aut}} ( \mathbf { P})$
. A nonempty collection
$\operatorname {\mathrm {Aut}} ( \mathbf { P})$
. A nonempty collection
![]() $\mathcal {F}$
of subgroups of
$\mathcal {F}$
of subgroups of
![]() $\mathcal {G}$
is a filter on
$\mathcal {G}$
is a filter on
![]() $\mathcal {G}$
if it is closed under supergroups and finite intersections. A filter
$\mathcal {G}$
if it is closed under supergroups and finite intersections. A filter
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\mathcal {G}$
is said to be normal if for every
$\mathcal {G}$
is said to be normal if for every
![]() $H \in \mathcal {F}$
and
$H \in \mathcal {F}$
and
![]() $\pi \in \mathcal {G}$
, the conjugated subgroup
$\pi \in \mathcal {G}$
, the conjugated subgroup
![]() $\pi H \pi ^{-1}$
belongs to
$\pi H \pi ^{-1}$
belongs to
![]() $\mathcal {F}$
as well.
$\mathcal {F}$
as well.
We say that the triple
![]() $\mathopen \langle \mathbf { P} , \mathcal {G} , \mathcal {F} \mathclose \rangle $
is a symmetric system if
$\mathopen \langle \mathbf { P} , \mathcal {G} , \mathcal {F} \mathclose \rangle $
is a symmetric system if
![]() $\mathbf { P}$
is a forcing notion,
$\mathbf { P}$
is a forcing notion,
![]() $\mathcal {G }$
is a subgroup of
$\mathcal {G }$
is a subgroup of
![]() $\operatorname {\mathrm {Aut}} ( \mathbf { P} )$
and
$\operatorname {\mathrm {Aut}} ( \mathbf { P} )$
and
![]() $\mathcal {F}$
is a normal filter on
$\mathcal {F}$
is a normal filter on
![]() $\mathcal {G}$
. Given a
$\mathcal {G}$
. Given a
![]() $\mathbf { P}$
-name
$\mathbf { P}$
-name
![]() $\dot {x}$
, we say that
$\dot {x}$
, we say that
![]() $\dot {x}$
is
$\dot {x}$
is
![]() $\mathcal {F}$
-symmetric if there exists
$\mathcal {F}$
-symmetric if there exists
![]() $H \in \mathcal {F}$
such that for all
$H \in \mathcal {F}$
such that for all
![]() $\pi \in H$
,
$\pi \in H$
,
![]() $\pi \dot {x} = \dot {x}$
. This definition extends by recursion:
$\pi \dot {x} = \dot {x}$
. This definition extends by recursion:
![]() $\dot {x}$
is hereditarily
$\dot {x}$
is hereditarily
![]() $\mathcal {F}$
-symmetric, if
$\mathcal {F}$
-symmetric, if
![]() $\dot {x}$
is
$\dot {x}$
is
![]() $\mathcal {F}$
-symmetric and every name
$\mathcal {F}$
-symmetric and every name
![]() $\dot {y} \in \operatorname {\mathrm {dom}} ( \dot {x} )$
is hereditarily
$\dot {y} \in \operatorname {\mathrm {dom}} ( \dot {x} )$
is hereditarily
![]() $\mathcal {F}$
-symmetric. We denote by
$\mathcal {F}$
-symmetric. We denote by
![]() $\mathsf {HS} _{\mathcal {F}}$
the class of all hereditarily
$\mathsf {HS} _{\mathcal {F}}$
the class of all hereditarily
![]() $\mathcal {F}$
-symmetric names.
$\mathcal {F}$
-symmetric names.
Theorem 3.2 [Reference Jech3, Lemma 15.51].
Suppose that
![]() $\mathopen \langle \mathbf { P} , \mathcal {G} , \mathcal {F} \mathclose \rangle $
is a symmetric system and
$\mathopen \langle \mathbf { P} , \mathcal {G} , \mathcal {F} \mathclose \rangle $
is a symmetric system and
![]() $G \subseteq \mathbf { P}$
is a
$G \subseteq \mathbf { P}$
is a
![]() $\mathord {\mathrm {V}}$
-generic filter. Denote by
$\mathord {\mathrm {V}}$
-generic filter. Denote by
![]() $\mathcal {N}$
the class
$\mathcal {N}$
the class
![]() $\mathopen \{{ \dot {x}_G }\boldsymbol \mid { \dot {x} \in \mathsf {HS} _{\mathcal {F}}} \mathclose \}$
, then
$\mathopen \{{ \dot {x}_G }\boldsymbol \mid { \dot {x} \in \mathsf {HS} _{\mathcal {F}}} \mathclose \}$
, then
![]() $\mathcal {N}$
is a transitive model of
$\mathcal {N}$
is a transitive model of
![]() $\mathsf {ZF}$
, and
$\mathsf {ZF}$
, and
![]() $\mathord {\mathrm {V}} \subseteq \mathcal {N} \subseteq \mathord {\mathrm {V}} [ G ]$
.
$\mathord {\mathrm {V}} \subseteq \mathcal {N} \subseteq \mathord {\mathrm {V}} [ G ]$
.
The class
![]() $\mathcal {N}$
is also known as a symmetric extension of
$\mathcal {N}$
is also known as a symmetric extension of
![]() $\mathord {\mathrm {V}}$
. Symmetric extensions are often used to produce models of
$\mathord {\mathrm {V}}$
. Symmetric extensions are often used to produce models of
![]() $\mathsf {ZF}$
in which the axiom of choice fails. We focus on this notion by discussing the construction due to Cohen of a symmetric extension in which there is an infinite, D-finite set of reals. This model will be the first step in the forcing iteration in Theorem 4.1.
$\mathsf {ZF}$
in which the axiom of choice fails. We focus on this notion by discussing the construction due to Cohen of a symmetric extension in which there is an infinite, D-finite set of reals. This model will be the first step in the forcing iteration in Theorem 4.1.
3.1 The first Cohen model
Let
![]() $\mathbf { P}_0$
be the forcing that adds countably many Cohen reals, i.e.,
$\mathbf { P}_0$
be the forcing that adds countably many Cohen reals, i.e.,
with
![]() $p \leq q$
if
$p \leq q$
if
![]() $\operatorname {\mathrm {dom}} ( p ) \supseteq \operatorname {\mathrm {dom}} ( q )$
and
$\operatorname {\mathrm {dom}} ( p ) \supseteq \operatorname {\mathrm {dom}} ( q )$
and
![]() $p ( n ) \supseteq q ( n )$
for all
$p ( n ) \supseteq q ( n )$
for all
![]() $n \in \operatorname {\mathrm {dom}} ( q )$
. Although this is not the standard presentation of such a forcing, this way of defining
$n \in \operatorname {\mathrm {dom}} ( q )$
. Although this is not the standard presentation of such a forcing, this way of defining
![]() $\mathbf { P}_0$
will become useful in the Section 4. Let
$\mathbf { P}_0$
will become useful in the Section 4. Let
![]() $\dot {a}_n$
be the canonical name for the nth Cohen real, that is,
$\dot {a}_n$
be the canonical name for the nth Cohen real, that is,
Observe that
![]() $\dot {A} \mathrel {{:}{=}} \mathopen \{{ \dot {a}_n }\boldsymbol \mid { n \in \omega } \mathclose \} ^\bullet $
is forced to be a dense subset of
$\dot {A} \mathrel {{:}{=}} \mathopen \{{ \dot {a}_n }\boldsymbol \mid { n \in \omega } \mathclose \} ^\bullet $
is forced to be a dense subset of
![]() ${}^ \omega 2$
.
${}^ \omega 2$
.
Every permutation
![]() $\pi $
on
$\pi $
on
![]() $\omega $
induces an automorphism of
$\omega $
induces an automorphism of
![]() $\mathbf { P}_0$
as follows: given
$\mathbf { P}_0$
as follows: given
![]() $p \in \mathbf { P}_0$
, we let
$p \in \mathbf { P}_0$
, we let
![]() $\pi p \in \mathbf { P}_0$
be defined by
$\pi p \in \mathbf { P}_0$
be defined by
We conflate the notation by using the same symbol
![]() $\pi $
to denote both the permutation and the automorphism on
$\pi $
to denote both the permutation and the automorphism on
![]() $\mathbf { P}_0$
it induces. Let
$\mathbf { P}_0$
it induces. Let
![]() $\mathcal {G}_0$
be the group of all such automorphisms. For every finite
$\mathcal {G}_0$
be the group of all such automorphisms. For every finite
![]() $E \subset \omega $
, let
$E \subset \omega $
, let
![]() $\operatorname {\mathrm {Fix}} ( E )$
be the subgroup of
$\operatorname {\mathrm {Fix}} ( E )$
be the subgroup of
![]() $\mathcal {G}_0$
of all those automorphisms induced by permutations that pointwise fix the set E. Let
$\mathcal {G}_0$
of all those automorphisms induced by permutations that pointwise fix the set E. Let
![]() $\mathcal {F}_0$
be the filter on
$\mathcal {F}_0$
be the filter on
![]() $\mathcal {G}_0$
generated by
$\mathcal {G}_0$
generated by
![]() $\mathopen \{{ \operatorname {\mathrm {Fix}} (E) }\boldsymbol \mid { E \subset \omega \text { finite} } \mathclose \}$
. It is easy to check that
$\mathopen \{{ \operatorname {\mathrm {Fix}} (E) }\boldsymbol \mid { E \subset \omega \text { finite} } \mathclose \}$
. It is easy to check that
![]() $\mathcal {F}_0$
is actually a normal filter on
$\mathcal {F}_0$
is actually a normal filter on
![]() $\mathcal {G}_0$
, and hence
$\mathcal {G}_0$
, and hence
![]() $\mathopen \langle \mathbf { P}_0 , \mathcal {G}_0 , \mathcal {F}_0 \mathclose \rangle $
is a symmetric system. Let G be a
$\mathopen \langle \mathbf { P}_0 , \mathcal {G}_0 , \mathcal {F}_0 \mathclose \rangle $
is a symmetric system. Let G be a
![]() $\mathord {\mathrm {V}}$
-generic filter for
$\mathord {\mathrm {V}}$
-generic filter for
![]() $\mathbf { P}_0$
, and let
$\mathbf { P}_0$
, and let
![]() $\mathcal {N}_0$
be the corresponding symmetric extension, which we call first Cohen model.
$\mathcal {N}_0$
be the corresponding symmetric extension, which we call first Cohen model.
Denote by A the realization of the name
![]() $\dot {A}$
in
$\dot {A}$
in
![]() $\mathord {\mathrm {V}} [ G ]$
, i.e., the set
$\mathord {\mathrm {V}} [ G ]$
, i.e., the set
![]() $\dot {A}_G$
. Note that every
$\dot {A}_G$
. Note that every
![]() $\dot {a}_n$
is in
$\dot {a}_n$
is in
![]() $\mathsf {HS} _{\mathcal {F}_0 }$
and so is
$\mathsf {HS} _{\mathcal {F}_0 }$
and so is
![]() $\dot {A}$
.
$\dot {A}$
.
Proposition 3.3 [Reference Jech3, Example 15.52]
![]() $\mathcal {N}_0 \vDash "A$
is D-finite”.
$\mathcal {N}_0 \vDash "A$
is D-finite”.
In
![]() $\mathcal {N}_0$
, the set A, being infinite and D-finite, is certainly not separable as a subspace of
$\mathcal {N}_0$
, the set A, being infinite and D-finite, is certainly not separable as a subspace of
![]() $\mathbb {R}$
—indeed, every infinite, separable
$\mathbb {R}$
—indeed, every infinite, separable
![]() $\mathrm {T}_1$
space is Dedekind-infinite. Moreover,
$\mathrm {T}_1$
space is Dedekind-infinite. Moreover,
![]() $ \mathsf {DC} ( A )$
also fails, as otherwise A would be Dedekind-infinite (see the penultimate paragraph of Section 2.2).
$ \mathsf {DC} ( A )$
also fails, as otherwise A would be Dedekind-infinite (see the penultimate paragraph of Section 2.2).
The simultaneous local failure of both
![]() ${\mathsf {AC}}_\omega $
and
${\mathsf {AC}}_\omega $
and
![]() $\mathsf {DC}$
is not accidental—the next proposition shows that, in the first Cohen model, any X such that
$\mathsf {DC}$
is not accidental—the next proposition shows that, in the first Cohen model, any X such that
![]() $\mathsf {DC} ( X )$
holds must be well-orderable, and hence
$\mathsf {DC} ( X )$
holds must be well-orderable, and hence
![]() ${\mathsf {AC}}_\omega ( X )$
holds.
${\mathsf {AC}}_\omega ( X )$
holds.
Proposition 3.4.
![]() $\mathcal {N}_0 \vDash \forall X \left ( \mathsf {DC} ( X ) \Rightarrow \mathsf {AC} (X) \right )$
.
$\mathcal {N}_0 \vDash \forall X \left ( \mathsf {DC} ( X ) \Rightarrow \mathsf {AC} (X) \right )$
.
Lemma 3.5. Let X be a linearly ordered set, and let
![]() $Y \subseteq [ X ]^{< \omega }$
. If
$Y \subseteq [ X ]^{< \omega }$
. If
![]() $\omega \precsim Y$
, then
$\omega \precsim Y$
, then
![]() $\omega \precsim \bigcup Y$
.
$\omega \precsim \bigcup Y$
.
Proof Let
![]() $\leq $
be a linear ordering of X, and let
$\leq $
be a linear ordering of X, and let
![]() $( Z_n )_{n \in \omega }$
be a sequence of distinct elements of Y. By passing to a subsequence, we may assume that
$( Z_n )_{n \in \omega }$
be a sequence of distinct elements of Y. By passing to a subsequence, we may assume that
![]() $Z_{ n + 1 } \nsubseteq Z_0 \cup \dots \cup Z_n$
, and that
$Z_{ n + 1 } \nsubseteq Z_0 \cup \dots \cup Z_n$
, and that
![]() $Z_0 \neq \emptyset $
. Let
$Z_0 \neq \emptyset $
. Let
![]() $z_0$
be the
$z_0$
be the
![]() $\le $
-least element of
$\le $
-least element of
![]() $Z_0$
, and
$Z_0$
, and
![]() $z_{ n + 1}$
be the
$z_{ n + 1}$
be the
![]() $\le $
-least element of
$\le $
-least element of
![]() $Z_{n + 1} \setminus ( Z_0 \cup \dots \cup Z_n )$
for every n. The
$Z_{n + 1} \setminus ( Z_0 \cup \dots \cup Z_n )$
for every n. The
![]() $z_n$
s are distinct, and belong to
$z_n$
s are distinct, and belong to
![]() $\bigcup Y$
, as required.
$\bigcup Y$
, as required.
Lemma 3.6. If
![]() $\mathsf {DC} ( Y )$
with
$\mathsf {DC} ( Y )$
with
![]() $Y \subseteq [ \mathbb {R} ]^{<\omega }$
infinite, then
$Y \subseteq [ \mathbb {R} ]^{<\omega }$
infinite, then
![]() $\omega \precsim \bigcup Y$
.
$\omega \precsim \bigcup Y$
.
Proof If
![]() $\bigcup Y$
has no limit points, then it is discrete, so
$\bigcup Y$
has no limit points, then it is discrete, so
![]() $\omega \precsim \bigcup Y$
. Suppose otherwise, and let
$\omega \precsim \bigcup Y$
. Suppose otherwise, and let
![]() $x \in \mathbb {R}$
be a limit point of
$x \in \mathbb {R}$
be a limit point of
![]() $\bigcup Y$
. It is enough to show that
$\bigcup Y$
. It is enough to show that
![]() $\omega \precsim Y$
and then apply Lemma 3.5 with
$\omega \precsim Y$
and then apply Lemma 3.5 with
![]() $X = \mathbb {R}$
. Without loss of generality, we may assume that
$X = \mathbb {R}$
. Without loss of generality, we may assume that
![]() $\mathopen \{ { x} \mathclose \} , \emptyset \notin Y$
. For all
$\mathopen \{ { x} \mathclose \} , \emptyset \notin Y$
. For all
![]() $Z \in Y$
let
$Z \in Y$
let
![]() $d ( x , Z ) = \min \mathopen \{{ | r - x | }\boldsymbol \mid { r \in Z \setminus \mathopen \{ { x } \mathclose \} } \mathclose \}$
be the distance of x from the rest of Z. Let
$d ( x , Z ) = \min \mathopen \{{ | r - x | }\boldsymbol \mid { r \in Z \setminus \mathopen \{ { x } \mathclose \} } \mathclose \}$
be the distance of x from the rest of Z. Let
![]() $R \subseteq Y ^2$
be the binary relation defined as follows: for every
$R \subseteq Y ^2$
be the binary relation defined as follows: for every
![]() $Z , W \in Y$
,
$Z , W \in Y$
,
The relation R is acyclic, and, by our hypothesis on x, it is total. It follows from
![]() $\mathsf {DC} ( Y )$
that R has an infinite chain, and hence
$\mathsf {DC} ( Y )$
that R has an infinite chain, and hence
![]() $\omega \precsim Y$
.
$\omega \precsim Y$
.
Proof of Proposition 3.4
In the first Cohen model, for every set X, there is a map
![]() $s_X \colon X \to [ A ]^{<\omega }$
, known as the least support map, such that
$s_X \colon X \to [ A ]^{<\omega }$
, known as the least support map, such that
![]() $s^{-1} ( \mathopen \{ { B } \mathclose \} )$
is well-orderable for every
$s^{-1} ( \mathopen \{ { B } \mathclose \} )$
is well-orderable for every
![]() $B \in [ A ]^{ < \omega }$
[Reference Jech2, Theorem 5.21 and Lemma 5.25].
$B \in [ A ]^{ < \omega }$
[Reference Jech2, Theorem 5.21 and Lemma 5.25].
Let X be such that
![]() $\mathsf {DC} ( X )$
holds. Then also
$\mathsf {DC} ( X )$
holds. Then also
![]() $\mathsf {DC} ( \operatorname {\mathrm {ran}} ( s_X ) )$
holds. If
$\mathsf {DC} ( \operatorname {\mathrm {ran}} ( s_X ) )$
holds. If
![]() $\operatorname {\mathrm {ran}} ( s_X )$
were infinite, then letting
$\operatorname {\mathrm {ran}} ( s_X )$
were infinite, then letting
![]() $Y= \operatorname {\mathrm {ran}} ( s_X )$
in Lemma 3.6 we would have
$Y= \operatorname {\mathrm {ran}} ( s_X )$
in Lemma 3.6 we would have
![]() $\omega \precsim \bigcup \operatorname {\mathrm {ran}} ( s_X ) \subseteq A$
, against the fact that A is D-finite. Hence
$\omega \precsim \bigcup \operatorname {\mathrm {ran}} ( s_X ) \subseteq A$
, against the fact that A is D-finite. Hence
![]() $\operatorname {\mathrm {ran}} ( s_X )$
is finite, and X, being a finite union of well-orderable sets, is well-orderable.
$\operatorname {\mathrm {ran}} ( s_X )$
is finite, and X, being a finite union of well-orderable sets, is well-orderable.
4 The main result
This section is devoted to proving the following:
Theorem 4.1. It is consistent with
![]() $\mathsf {ZF}$
that there is a set
$\mathsf {ZF}$
that there is a set
![]() $A \subseteq \mathbb {R}$
such that
$A \subseteq \mathbb {R}$
such that
![]() $\mathsf {DC} ( A )$
and
$\mathsf {DC} ( A )$
and
![]() $\neg {\mathsf {AC}}_\omega ( A )$
.
$\neg {\mathsf {AC}}_\omega ( A )$
.
4.1 Outline of the proof
We prove the theorem via an iteration of symmetric extensions of length
![]() $\omega $
. We start the iteration with the first Cohen model
$\omega $
. We start the iteration with the first Cohen model
![]() $\mathcal {N}_0$
, with
$\mathcal {N}_0$
, with
![]() $A \in \mathcal {N}_0$
being the generic D-finite set of reals (see Section 3.1). As noted right after Proposition 3.3, in
$A \in \mathcal {N}_0$
being the generic D-finite set of reals (see Section 3.1). As noted right after Proposition 3.3, in
![]() $\mathcal {N}_0$
the set A is not separable (in particular
$\mathcal {N}_0$
the set A is not separable (in particular
![]() ${\mathsf {AC}}_\omega ( A )$
fails) and
${\mathsf {AC}}_\omega ( A )$
fails) and
![]() $\mathsf {DC} ( A )$
fails. Next, we define a chain of models
$\mathsf {DC} ( A )$
fails. Next, we define a chain of models
![]() $\mathcal {N}_0 \subset \mathcal {N}_1 \subset \dots \subset \mathcal {N}_\omega $
such that, for each n,
$\mathcal {N}_0 \subset \mathcal {N}_1 \subset \dots \subset \mathcal {N}_\omega $
such that, for each n,
![]() $\mathcal {N}_{n+1}$
is a symmetric extension of
$\mathcal {N}_{n+1}$
is a symmetric extension of
![]() $\mathcal {N}_n$
that contains a generic set of chains for all binary relations in
$\mathcal {N}_n$
that contains a generic set of chains for all binary relations in
![]() $\mathcal {N}_n$
that are total and acyclic on A. At the final stage,
$\mathcal {N}_n$
that are total and acyclic on A. At the final stage,
![]() $\mathcal {N}_\omega $
, which is our model, is going to be something resembling “the model of sets definable from finitely many elements of
$\mathcal {N}_\omega $
, which is our model, is going to be something resembling “the model of sets definable from finitely many elements of
![]() $\bigcup _n \mathcal {N}_n$
”. If we do the construction properly, we can prove that in
$\bigcup _n \mathcal {N}_n$
”. If we do the construction properly, we can prove that in
![]() $\mathcal {N}_\omega $
we have added enough countable subsets of A (or, equivalently, enough sequences over A) to guarantee
$\mathcal {N}_\omega $
we have added enough countable subsets of A (or, equivalently, enough sequences over A) to guarantee
![]() $\mathsf {DC} ( A )$
(Theorem 4.10), but A is still not separable, in particular
$\mathsf {DC} ( A )$
(Theorem 4.10), but A is still not separable, in particular
![]() ${\mathsf {AC}}_\omega ( A )$
fails (Corollary 4.8).
${\mathsf {AC}}_\omega ( A )$
fails (Corollary 4.8).
Actually, we don’t only show that A is not separable in our model, but we give a topological characterization of its separable subsets: among the subsets of A, the separable ones are precisely those which are scattered with finite scattered height (Definition 4.5 and Theorem 4.7).
4.2 The symmetric system
We define recursively a sequence
![]() $\mathopen \langle \mathbf { P}_n , \mathcal {G}_n , \mathcal {F}_n \mathclose \rangle _{ n \in \omega }$
of symmetric systems. Let
$\mathopen \langle \mathbf { P}_n , \mathcal {G}_n , \mathcal {F}_n \mathclose \rangle _{ n \in \omega }$
of symmetric systems. Let
![]() $\mathopen \langle \mathbf { P}_0 , \mathcal {G}_0 , \mathcal {F}_0 \mathclose \rangle $
be the symmetric system defined in Section 3.1, i.e., the one that induces the first Cohen model. For each n we denote by
$\mathopen \langle \mathbf { P}_0 , \mathcal {G}_0 , \mathcal {F}_0 \mathclose \rangle $
be the symmetric system defined in Section 3.1, i.e., the one that induces the first Cohen model. For each n we denote by
![]() $\leq _n, \Vdash _n$
the ordering and the forcing relation of
$\leq _n, \Vdash _n$
the ordering and the forcing relation of
![]() $\mathbf { P}_n$
, respectively, and by
$\mathbf { P}_n$
, respectively, and by
![]() $\mathsf {HS} _n$
the class
$\mathsf {HS} _n$
the class
![]() $\mathsf {HS} _{ \mathcal {F}_n }$
, i.e., the class of all hereditarily
$\mathsf {HS} _{ \mathcal {F}_n }$
, i.e., the class of all hereditarily
![]() $\mathcal {F}_n$
-symmetric
$\mathcal {F}_n$
-symmetric
![]() $\mathbf { P} _n$
-names. We also let
$\mathbf { P} _n$
-names. We also let
where the
![]() $\dot {a}_i$
s are as in (4). Then
$\dot {a}_i$
s are as in (4). Then
![]() $\mathcal {R}_n$
is the set of all “good” hereditarily
$\mathcal {R}_n$
is the set of all “good” hereditarily
![]() $\mathcal {F}_n$
-symmetric
$\mathcal {F}_n$
-symmetric
![]() $\mathbf { P} _n$
-names for binary relations on
$\mathbf { P} _n$
-names for binary relations on
![]() $\dot {A}$
.
$\dot {A}$
.
Recursively on n, we define
![]() $\mathbf { P} _{n+1}$
to be the set of all the sequences
$\mathbf { P} _{n+1}$
to be the set of all the sequences
![]() $p = \mathopen \langle p_k \boldsymbol \mid k \leq n + 1 \mathclose \rangle $
such that:
$p = \mathopen \langle p_k \boldsymbol \mid k \leq n + 1 \mathclose \rangle $
such that:
-
(1)
 $p {\mathop {\upharpoonright }} n + 1 \in \mathbf { P} _{n}$
.
$p {\mathop {\upharpoonright }} n + 1 \in \mathbf { P} _{n}$
. -
(2)
 $p_{n+1} \colon \operatorname {\mathrm {dom}} ( p_{n + 1 } ) \to \mathcal {R}_n \times {}^{<\omega } \omega $
with
$p_{n+1} \colon \operatorname {\mathrm {dom}} ( p_{n + 1 } ) \to \mathcal {R}_n \times {}^{<\omega } \omega $
with
 $\operatorname {\mathrm {dom}} ( p_{n+1} )$
a finite subset of
$\operatorname {\mathrm {dom}} ( p_{n+1} )$
a finite subset of
 $\omega $
.
$\omega $
. -
(3) For each
 $k \in \operatorname {\mathrm {dom}} ( p_{n + 1 } )$
with
$k \in \operatorname {\mathrm {dom}} ( p_{n + 1 } )$
with
 $p_{n+1} ( k ) = ( \dot {R}, \mathopen \langle m_0 , \dots , m_h \mathclose \rangle )$
we have
$p_{n+1} ( k ) = ( \dot {R}, \mathopen \langle m_0 , \dots , m_h \mathclose \rangle )$
we have  $$\begin{align*}p {\mathop{\upharpoonright}} n + 1 \Vdash _n "\dot{R} \text{ is total, acyclic and }\dot{a}_{ m_0 } \mathrel{\dot{R}} \dot{a}_{ m_1 } \mathrel{\dot{R}} \dots \mathrel{\dot{R}} \dot{a}_{ m_h }", \end{align*}$$
$$\begin{align*}p {\mathop{\upharpoonright}} n + 1 \Vdash _n "\dot{R} \text{ is total, acyclic and }\dot{a}_{ m_0 } \mathrel{\dot{R}} \dot{a}_{ m_1 } \mathrel{\dot{R}} \dots \mathrel{\dot{R}} \dot{a}_{ m_h }", \end{align*}$$
where, at stage
![]() $n = 0$
, we identify the conditions
$n = 0$
, we identify the conditions
![]() $p \in \mathbf { P} _0$
with their singleton sequence
$p \in \mathbf { P} _0$
with their singleton sequence
![]() $\mathopen \langle p \mathclose \rangle $
.
$\mathopen \langle p \mathclose \rangle $
.
For each
![]() $p \in \mathbf { P} _{n+1}$
and
$p \in \mathbf { P} _{n+1}$
and
![]() $k \in \operatorname {\mathrm {dom}} ( p_{ n + 1 } )$
with
$k \in \operatorname {\mathrm {dom}} ( p_{ n + 1 } )$
with
![]() $p_{ n + 1 } ( k ) = ( \dot {R} , s )$
, we denote
$p_{ n + 1 } ( k ) = ( \dot {R} , s )$
, we denote
![]() $\dot {R}$
and s by
$\dot {R}$
and s by
![]() $p_{n + 1}^R ( k )$
and
$p_{n + 1}^R ( k )$
and
![]() $p_{n + 1}^s ( k )$
, respectively. Given
$p_{n + 1}^s ( k )$
, respectively. Given
![]() $p , q \in \mathbf { P} _{ n + 1 }$
we let
$p , q \in \mathbf { P} _{ n + 1 }$
we let
![]() $p \leq _{ n + 1 } q$
if and only if:
$p \leq _{ n + 1 } q$
if and only if:
-
•
 $p {\mathop {\upharpoonright }} n + 1 \leq _n q {\mathop {\upharpoonright }} n + 1$
,
$p {\mathop {\upharpoonright }} n + 1 \leq _n q {\mathop {\upharpoonright }} n + 1$
, -
•
 $\operatorname {\mathrm {dom}} ( p_{n + 1} ) \supseteq \operatorname {\mathrm {dom}} ( q_{n + 1 } )$
,
$\operatorname {\mathrm {dom}} ( p_{n + 1} ) \supseteq \operatorname {\mathrm {dom}} ( q_{n + 1 } )$
, -
•
 $\forall { k \in \operatorname {\mathrm {dom}} ( q_{n + 1 } ) } \, ( p_{n + 1 }^R ( k ) = q_{ n + 1 }^R ( k )$
and
$\forall { k \in \operatorname {\mathrm {dom}} ( q_{n + 1 } ) } \, ( p_{n + 1 }^R ( k ) = q_{ n + 1 }^R ( k )$
and
 $p_{ n + 1 }^s ( k ) \supseteq q_{n + 1 }^s ( k ))$
.
$p_{ n + 1 }^s ( k ) \supseteq q_{n + 1 }^s ( k ))$
.
This defines the forcing
![]() $\mathbf { P} _{n + 1}$
. Now we are left to define the subgroup
$\mathbf { P} _{n + 1}$
. Now we are left to define the subgroup
![]() $\mathcal {G}_{ n + 1 }$
of
$\mathcal {G}_{ n + 1 }$
of
![]() $\operatorname {\mathrm {Aut}} ( \mathbf { P} _{n + 1 } )$
, and the filter
$\operatorname {\mathrm {Aut}} ( \mathbf { P} _{n + 1 } )$
, and the filter
![]() $\mathcal {F}_{ n + 1 }$
.
$\mathcal {F}_{ n + 1 }$
.
Consider a sequence
![]() $\vec {\pi } = \mathopen \langle \pi _0, \dots , \pi _{ n + 1 } \mathclose \rangle $
with each
$\vec {\pi } = \mathopen \langle \pi _0, \dots , \pi _{ n + 1 } \mathclose \rangle $
with each
![]() $\pi _i$
being a permutation of
$\pi _i$
being a permutation of
![]() $\omega $
. By induction hypothesisFootnote
1
$\omega $
. By induction hypothesisFootnote
1
induces an automorphism
![]() $\vec { \rho } \in \mathcal {G}_n$
. Note that, as in Section 3.1, we conflate the notation by using the same symbol to denote both sequences of permutations and the automorphisms they induce. Now, the sequence
$\vec { \rho } \in \mathcal {G}_n$
. Note that, as in Section 3.1, we conflate the notation by using the same symbol to denote both sequences of permutations and the automorphisms they induce. Now, the sequence
![]() $\vec {\pi }$
induces an automorphism on
$\vec {\pi }$
induces an automorphism on
![]() $\mathbf { P} _{ n + 1 }$
as follows: given
$\mathbf { P} _{ n + 1 }$
as follows: given
![]() $p \in \mathbf { P} _{ n + 1 }$
, we let
$p \in \mathbf { P} _{ n + 1 }$
, we let
![]() $\vec {\pi } p$
be the condition in
$\vec {\pi } p$
be the condition in
![]() $\mathbf { P} _{ n + 1 }$
such that
$\mathbf { P} _{ n + 1 }$
such that
![]() $( \vec {\pi } p ) {\mathop {\upharpoonright }} n + 1 = \vec {\rho } ( p {\mathop {\upharpoonright }} n + 1)$
and, for each
$( \vec {\pi } p ) {\mathop {\upharpoonright }} n + 1 = \vec {\rho } ( p {\mathop {\upharpoonright }} n + 1)$
and, for each
![]() $k \in \operatorname {\mathrm {dom}} ( p_{ n + 1 } )$
with
$k \in \operatorname {\mathrm {dom}} ( p_{ n + 1 } )$
with
![]() $p_{ n + 1 }^s ( k ) = \mathopen \langle m_0 , \dots , m_h \mathclose \rangle $
and
$p_{ n + 1 }^s ( k ) = \mathopen \langle m_0 , \dots , m_h \mathclose \rangle $
and
![]() $p_{ n + 1 }^R ( k ) = \dot {R}$
,
$p_{ n + 1 }^R ( k ) = \dot {R}$
,
 $$ \begin{align*} ( \vec{\pi} p )_{ n + 1 }^R ( \pi_{ n + 1 } ( k ) ) & = \vec{\rho} ( \dot{R} ) , \\ ( \vec{\pi} p )_{ n + 1 }^s ( \pi_{ n + 1 } ( k ) ) & = \mathopen \langle \pi_0 ( m_0 ) , \dots, \pi_0 ( m_h ) \mathclose \rangle. \end{align*} $$
$$ \begin{align*} ( \vec{\pi} p )_{ n + 1 }^R ( \pi_{ n + 1 } ( k ) ) & = \vec{\rho} ( \dot{R} ) , \\ ( \vec{\pi} p )_{ n + 1 }^s ( \pi_{ n + 1 } ( k ) ) & = \mathopen \langle \pi_0 ( m_0 ) , \dots, \pi_0 ( m_h ) \mathclose \rangle. \end{align*} $$
Let
![]() $\mathcal {G}_{n + 1}$
be the group of all such automorphisms on
$\mathcal {G}_{n + 1}$
be the group of all such automorphisms on
![]() $\mathbf { P} _{n + 1}$
, i.e., the ones induced by sequences (of length
$\mathbf { P} _{n + 1}$
, i.e., the ones induced by sequences (of length
![]() $n + 2$
) of permutations of
$n + 2$
) of permutations of
![]() $\omega $
. For each sequence
$\omega $
. For each sequence
![]() ${\vec {H} = \mathopen \langle H_0 , \dots , H_{ n + 1 } \mathclose \rangle }$
of subsets of
${\vec {H} = \mathopen \langle H_0 , \dots , H_{ n + 1 } \mathclose \rangle }$
of subsets of
![]() $\omega $
, we let
$\omega $
, we let
![]() $\operatorname {\mathrm {Fix}} ( \vec {H} )$
be the subgroup of all those
$\operatorname {\mathrm {Fix}} ( \vec {H} )$
be the subgroup of all those
![]() $\vec {\pi } \in \mathcal {G}_{n + 1}$
such that
$\vec {\pi } \in \mathcal {G}_{n + 1}$
such that
![]() $\pi _k$
pointwise fixes
$\pi _k$
pointwise fixes
![]() $H_k$
for all
$H_k$
for all
![]() $k \leq n + 1$
. We define
$k \leq n + 1$
. We define
![]() $\mathcal {F}_{n + 1}$
as the filter on
$\mathcal {F}_{n + 1}$
as the filter on
![]() $\mathcal {G}_{n + 1}$
generated by
$\mathcal {G}_{n + 1}$
generated by
![]() $\mathopen \{{ \operatorname {\mathrm {Fix}} ( \vec {H} ) }\boldsymbol \mid { H_k \text { is finite for all } k \leq n +1 } \mathclose \}$
. From now on, we use the symbol
$\mathopen \{{ \operatorname {\mathrm {Fix}} ( \vec {H} ) }\boldsymbol \mid { H_k \text { is finite for all } k \leq n +1 } \mathclose \}$
. From now on, we use the symbol
![]() $\vec {H}$
to denote finite sequences of finite subsets of
$\vec {H}$
to denote finite sequences of finite subsets of
![]() $\omega $
.
$\omega $
.
This ends the inductive definition of the sequence
![]() $\mathopen \langle \mathbf { P} _n , \mathcal {G}_n , \mathcal {F}_n \mathclose \rangle _{ n \in \omega }$
. Note that, for each
$\mathopen \langle \mathbf { P} _n , \mathcal {G}_n , \mathcal {F}_n \mathclose \rangle _{ n \in \omega }$
. Note that, for each
![]() $n < m$
, there is a natural complete embedding
$n < m$
, there is a natural complete embedding
![]() $i_{ n , m } \colon \mathbf { P} _n \to \mathbf { P} _m$
and a natural embedding
$i_{ n , m } \colon \mathbf { P} _n \to \mathbf { P} _m$
and a natural embedding
![]() $j_{ n , m } \colon \mathcal {G}_n \to \mathcal {G}_m$
. Thus we let
$j_{ n , m } \colon \mathcal {G}_n \to \mathcal {G}_m$
. Thus we let
![]() $\mathbf { P}$
and
$\mathbf { P}$
and
![]() $\mathcal {G}$
be the direct limits of the forcings
$\mathcal {G}$
be the direct limits of the forcings
![]() $\mathbf { P} _n$
and of the groups
$\mathbf { P} _n$
and of the groups
![]() $\mathcal {G}_n$
, respectively.
$\mathcal {G}_n$
, respectively.
We now define the normal filter
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\mathcal {G}$
in the expected way: we let
$\mathcal {G}$
in the expected way: we let
![]() $\mathcal {F}$
be the filter generated by
$\mathcal {F}$
be the filter generated by
where, given any
![]() $\vec {H}$
,
$\vec {H}$
,
![]() $\operatorname {\mathrm {Fix}} ( \vec {H} )$
is the subgroup of
$\operatorname {\mathrm {Fix}} ( \vec {H} )$
is the subgroup of
![]() $\mathcal {G}$
made of all those
$\mathcal {G}$
made of all those
![]() $\vec {\pi }$
such that
$\vec {\pi }$
such that
![]() $\pi _k$
pointwise fixes
$\pi _k$
pointwise fixes
![]() $H_k$
for all
$H_k$
for all
![]() $k < \operatorname {\mathrm {lh}} ( \vec {H} )$
.
$k < \operatorname {\mathrm {lh}} ( \vec {H} )$
.
A condition p of the direct limit
![]() $\mathbf { P}$
is a finite sequence
$\mathbf { P}$
is a finite sequence
![]() $\mathopen \langle p_0, \dots , p_n \mathclose \rangle $
, and it is identified with
$\mathopen \langle p_0, \dots , p_n \mathclose \rangle $
, and it is identified with
![]() $\mathopen \langle p_0, \dots , p_n , \emptyset , \dots , \emptyset \mathclose \rangle $
and with
$\mathopen \langle p_0, \dots , p_n , \emptyset , \dots , \emptyset \mathclose \rangle $
and with
![]() $\mathopen \langle p_0, \dots , p_n, \emptyset , \emptyset \dots \mathclose \rangle $
, that is a sequence obtained by concatenating p with a finite sequence of empty sets or with the infinite sequence of empty sets. We treat analogously the
$\mathopen \langle p_0, \dots , p_n, \emptyset , \emptyset \dots \mathclose \rangle $
, that is a sequence obtained by concatenating p with a finite sequence of empty sets or with the infinite sequence of empty sets. We treat analogously the
![]() $\vec {H}$
s.
$\vec {H}$
s.
Henceforth
![]() $\mathopen \langle \mathbf { P} , \mathcal {G}, \mathcal {F} \mathclose \rangle $
is our symmetric system, with
$\mathopen \langle \mathbf { P} , \mathcal {G}, \mathcal {F} \mathclose \rangle $
is our symmetric system, with
![]() $\mathsf {HS}$
being the class of all
$\mathsf {HS}$
being the class of all
![]() $\mathcal {F}$
-symmetric
$\mathcal {F}$
-symmetric
![]() $\mathbf { P}$
-names and
$\mathbf { P}$
-names and
![]() $\leq , \Vdash $
being the ordering and the forcing relation of
$\leq , \Vdash $
being the ordering and the forcing relation of
![]() $\mathbf { P}$
, respectively.
$\mathbf { P}$
, respectively.
Remark 4.2. Our iterative construction fits into the general framework developed by Asaf Karagila [Reference Karagila5] to deal with iterations of symmetric extensions.
Given an
![]() $\dot {x} \in \mathsf {HS}$
, we say that
$\dot {x} \in \mathsf {HS}$
, we say that
![]() $\vec {H}$
is a support of
$\vec {H}$
is a support of
![]() $\dot {x}$
if
$\dot {x}$
if
![]() $\vec {\pi } \dot {x} = \dot {x}$
for all
$\vec {\pi } \dot {x} = \dot {x}$
for all
![]() $\vec {\pi } \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. Also, given
$\vec {\pi } \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. Also, given
![]() $p = \mathopen \langle p_0, \dots , p_{n} \mathclose \rangle \in \mathbf { P}$
and
$p = \mathopen \langle p_0, \dots , p_{n} \mathclose \rangle \in \mathbf { P}$
and
![]() $\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
, we write
$\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
, we write
![]() $p {\mathop {\upharpoonright }} \vec {H}$
to denote the sequence
$p {\mathop {\upharpoonright }} \vec {H}$
to denote the sequence
![]() $\mathopen \langle p_0 {\mathop {\upharpoonright }} H_0 , \dots , p_{n} {\mathop {\upharpoonright }} H_{n} \mathclose \rangle $
. Note that the latter sequence needs not to belong to
$\mathopen \langle p_0 {\mathop {\upharpoonright }} H_0 , \dots , p_{n} {\mathop {\upharpoonright }} H_{n} \mathclose \rangle $
. Note that the latter sequence needs not to belong to
![]() $\mathbf { P}$
.
$\mathbf { P}$
.
Lemma 4.3 (Restriction Lemma).
Let ![]() be a formula in the forcing language, and let
be a formula in the forcing language, and let
![]() $\dot {x}_1,\dots , \dot {x}_n \in \mathsf {HS}$
. For any
$\dot {x}_1,\dots , \dot {x}_n \in \mathsf {HS}$
. For any
![]() $p \in \mathbf { P}$
and for any
$p \in \mathbf { P}$
and for any
![]() $\vec {H}$
, if
$\vec {H}$
, if
![]() $\vec {H}$
is a support for each of the
$\vec {H}$
is a support for each of the
![]() $\dot {x}_i$
’s and, for all
$\dot {x}_i$
’s and, for all
![]() $m> 0$
, for all
$m> 0$
, for all
![]() $k \in H_m \cap \operatorname {\mathrm {dom}} (p_m)$
,
$k \in H_m \cap \operatorname {\mathrm {dom}} (p_m)$
,
![]() $\vec {H} {\mathop {\upharpoonright }} m$
is a support for
$\vec {H} {\mathop {\upharpoonright }} m$
is a support for
![]() $ p^R_m ( k )$
and
$ p^R_m ( k )$
and
![]() $\operatorname {\mathrm {ran}} ( p^s_m ( k ) ) \subseteq H_0$
, then
$\operatorname {\mathrm {ran}} ( p^s_m ( k ) ) \subseteq H_0$
, then
![]() $p {\mathop {\upharpoonright }} \vec {H} \in \mathbf { P}$
and
$p {\mathop {\upharpoonright }} \vec {H} \in \mathbf { P}$
and
Proof We prove the lemma by induction on the length of
![]() $\vec {H}$
.
$\vec {H}$
.
Let’s first assume
![]() $\vec {H} = \mathopen \langle H_0 \mathclose \rangle $
for some finite
$\vec {H} = \mathopen \langle H_0 \mathclose \rangle $
for some finite
![]() $H_0\subset \omega $
, then
$H_0\subset \omega $
, then
![]() $p {\mathop {\upharpoonright }} \vec {H} \in \mathbf { P} _0$
. Assume for a contradiction that
$p {\mathop {\upharpoonright }} \vec {H} \in \mathbf { P} _0$
. Assume for a contradiction that ![]() , then there is a
, then there is a
![]() $q \leq p {\mathop {\upharpoonright }} \vec {H}$
such that
$q \leq p {\mathop {\upharpoonright }} \vec {H}$
such that ![]() . Let
. Let
![]() $\vec {\pi } \in \mathcal {G}$
such that
$\vec {\pi } \in \mathcal {G}$
such that
![]() $\pi _0$
pointwise fixes
$\pi _0$
pointwise fixes
![]() $H_0$
and such that
$H_0$
and such that
![]() $\pi _0[ \operatorname {\mathrm {dom}} (q_0)] \cap \operatorname {\mathrm {dom}} (p_0) = H_0 \cap \operatorname {\mathrm {dom}} (p_0)$
and
$\pi _0[ \operatorname {\mathrm {dom}} (q_0)] \cap \operatorname {\mathrm {dom}} (p_0) = H_0 \cap \operatorname {\mathrm {dom}} (p_0)$
and
![]() $\pi _m[ \operatorname {\mathrm {dom}} (q_m)] \cap \operatorname {\mathrm {dom}} (p_m) = \emptyset $
for all
$\pi _m[ \operatorname {\mathrm {dom}} (q_m)] \cap \operatorname {\mathrm {dom}} (p_m) = \emptyset $
for all
![]() $m> 0$
. In particular,
$m> 0$
. In particular,
![]() $\vec {\pi } \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. By hypothesis,
$\vec {\pi } \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. By hypothesis,
![]() $\vec {H}$
is a support for all the
$\vec {H}$
is a support for all the
![]() $\dot {x}_i$
’s. Thus, by the Symmetry Lemma,
$\dot {x}_i$
’s. Thus, by the Symmetry Lemma, ![]() . However, p and
. However, p and
![]() $\vec {\pi } q$
are compatible, contradiction.
$\vec {\pi } q$
are compatible, contradiction.
Now let’s assume that
![]() $\vec {H} = \mathopen \langle H_0, \dots , H_m \mathclose \rangle $
.
$\vec {H} = \mathopen \langle H_0, \dots , H_m \mathclose \rangle $
.
Claim 4.3.1.
![]() $p {\mathop {\upharpoonright }} \vec {H} \in \mathbf {P}_m$
.
$p {\mathop {\upharpoonright }} \vec {H} \in \mathbf {P}_m$
.
Proof By induction hypothesis,
![]() $p {\mathop {\upharpoonright }} ( \vec {H} {\mathop {\upharpoonright }} m ) \in \mathbf {P}_{ m - 1 }$
. Fix a
$p {\mathop {\upharpoonright }} ( \vec {H} {\mathop {\upharpoonright }} m ) \in \mathbf {P}_{ m - 1 }$
. Fix a
![]() $k \in H_m \cap \operatorname {\mathrm {dom}} (p_m)$
. Let
$k \in H_m \cap \operatorname {\mathrm {dom}} (p_m)$
. Let
![]() $\dot {R} = p_m^R ( k )$
and
$\dot {R} = p_m^R ( k )$
and
![]() $\mathopen \langle n_0 , \dots , n_h \mathclose \rangle = p_m^s ( k )$
. Then, by assumption,
$\mathopen \langle n_0 , \dots , n_h \mathclose \rangle = p_m^s ( k )$
. Then, by assumption,
![]() $\vec {H}{\mathop {\upharpoonright }} m$
is a support of
$\vec {H}{\mathop {\upharpoonright }} m$
is a support of
![]() $\dot {R}$
and
$\dot {R}$
and
![]() $n_i \in H_0$
for every
$n_i \in H_0$
for every
![]() $i \le h$
, or, equivalently,
$i \le h$
, or, equivalently,
![]() $H_0$
is a support for
$H_0$
is a support for
![]() $\dot {a}_{n_i}$
. By definition of
$\dot {a}_{n_i}$
. By definition of
![]() $\mathbf {P}_m$
,
$\mathbf {P}_m$
,
By induction hypothesis,
Therefore,
![]() $p {\mathop {\upharpoonright }} \vec {H} \in \mathbf {P}_m$
.
$p {\mathop {\upharpoonright }} \vec {H} \in \mathbf {P}_m$
.
Assume for a contradiction that ![]() , then there is a
, then there is a
![]() $q \leq p {\mathop {\upharpoonright }} \vec {H}$
such that
$q \leq p {\mathop {\upharpoonright }} \vec {H}$
such that ![]() . Let
. Let
![]() $\vec {\pi } \in \mathcal {G}$
such that
$\vec {\pi } \in \mathcal {G}$
such that
![]() $\pi _l$
pointwise fixes
$\pi _l$
pointwise fixes
![]() $H_l$
for each
$H_l$
for each
![]() $l \leq m$
and such that
$l \leq m$
and such that
![]() $\pi _l [ \operatorname {\mathrm {dom}} ( q_l ) ] \cap \operatorname {\mathrm {dom}} ( p_l ) = H_l \cap \operatorname {\mathrm {dom}} ( p_l )$
for all
$\pi _l [ \operatorname {\mathrm {dom}} ( q_l ) ] \cap \operatorname {\mathrm {dom}} ( p_l ) = H_l \cap \operatorname {\mathrm {dom}} ( p_l )$
for all
![]() $l \leq m$
and
$l \leq m$
and
![]() $\pi _l [ \operatorname {\mathrm {dom}} ( q_l ) ] \cap \operatorname {\mathrm {dom}} ( p_l ) = \emptyset $
for all
$\pi _l [ \operatorname {\mathrm {dom}} ( q_l ) ] \cap \operatorname {\mathrm {dom}} ( p_l ) = \emptyset $
for all
![]() $l> m$
. In particular,
$l> m$
. In particular,
![]() $\vec {\pi } \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. Thus, by the Symmetry Lemma,
$\vec {\pi } \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. Thus, by the Symmetry Lemma, ![]() .
.
Claim 4.3.2.
p and
![]() $\vec {\pi } q$
are compatible.
$\vec {\pi } q$
are compatible.
Proof It suffices to show that
![]() $p_l^R ( k ) = ( \vec {\pi } q )_l^R ( k )$
and that the sequence
$p_l^R ( k ) = ( \vec {\pi } q )_l^R ( k )$
and that the sequence
![]() $p_l^s ( k )$
is extended by
$p_l^s ( k )$
is extended by
![]() $( \vec {\pi } q)_l^s ( k )$
, for every
$( \vec {\pi } q)_l^s ( k )$
, for every
![]() $l \le m$
and for every
$l \le m$
and for every
![]() $k \in \operatorname {\mathrm {dom}} ( p_l ) \cap \operatorname {\mathrm {dom}} ( ( \vec { \pi } q )_l )$
. Note that
$k \in \operatorname {\mathrm {dom}} ( p_l ) \cap \operatorname {\mathrm {dom}} ( ( \vec { \pi } q )_l )$
. Note that
![]() $\operatorname {\mathrm {dom}} ( ( \vec {\pi } q )_l ) = \pi _l [ \operatorname {\mathrm {dom}} ( q_l ) ]$
. Fix an
$\operatorname {\mathrm {dom}} ( ( \vec {\pi } q )_l ) = \pi _l [ \operatorname {\mathrm {dom}} ( q_l ) ]$
. Fix an
![]() $l \le m$
and a
$l \le m$
and a
![]() $k \in \operatorname {\mathrm {dom}} ( p_l ) \cap \pi _l [ \operatorname {\mathrm {dom}} ( q_l )]$
. By the way we chose
$k \in \operatorname {\mathrm {dom}} ( p_l ) \cap \pi _l [ \operatorname {\mathrm {dom}} ( q_l )]$
. By the way we chose
![]() $\vec {\pi }$
, we must have
$\vec {\pi }$
, we must have
![]() $k \in H_l$
. Also, as we assumed
$k \in H_l$
. Also, as we assumed
![]() $q \le p$
, we have
$q \le p$
, we have
![]() $q_l^R ( k ) = p_l^R ( k )$
and
$q_l^R ( k ) = p_l^R ( k )$
and
![]() $q_l^s ( k ) \supseteq p_l^s ( k )$
. Moreover, we assumed
$q_l^s ( k ) \supseteq p_l^s ( k )$
. Moreover, we assumed
![]() $\vec {H} {\mathop {\upharpoonright }} l$
to be a support for
$\vec {H} {\mathop {\upharpoonright }} l$
to be a support for
![]() $p_l^R ( k )$
, and we have picked
$p_l^R ( k )$
, and we have picked
![]() $\vec {\pi }$
so that
$\vec {\pi }$
so that
![]() $\vec {\pi } \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. In particular,
$\vec {\pi } \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. In particular,
![]() $(\vec {\pi } {\mathop {\upharpoonright }} l) \, ( p_l^R ( k ) ) = p_l^R ( k )$
and
$(\vec {\pi } {\mathop {\upharpoonright }} l) \, ( p_l^R ( k ) ) = p_l^R ( k )$
and
![]() $\pi _l ( k ) = k$
. Therefore, by the definition of the induced automorphism
$\pi _l ( k ) = k$
. Therefore, by the definition of the induced automorphism
![]() $\vec {\pi } \in \mathcal {G}$
,
$\vec {\pi } \in \mathcal {G}$
,
Moreover, since we assumed
![]() $\operatorname {\mathrm {ran}} ( p_l^s ( k ) ) \subseteq H_0$
, and
$\operatorname {\mathrm {ran}} ( p_l^s ( k ) ) \subseteq H_0$
, and
![]() $\pi _0 \in \operatorname {\mathrm {Fix}} ( H_0 )$
, we have, for every
$\pi _0 \in \operatorname {\mathrm {Fix}} ( H_0 )$
, we have, for every
![]() $i< \operatorname {\mathrm {lh}} ( p_l^s ( k ) )$
,
$i< \operatorname {\mathrm {lh}} ( p_l^s ( k ) )$
,
and therefore
![]() $( \vec {\pi } q )_l^s ( k ) \supseteq p_l^s ( k )$
.
$( \vec {\pi } q )_l^s ( k ) \supseteq p_l^s ( k )$
.
As before, the fact that p and
![]() $\vec {\pi } q$
are compatible yields the desired contradiction and concludes the proof.
$\vec {\pi } q$
are compatible yields the desired contradiction and concludes the proof.
4.3 The model
For each
![]() $n , k \in \omega $
, we let
$n , k \in \omega $
, we let
 $$ \begin{align*} \dot{f}_{ n , k } &= \mathopen \{{ ( ( \check{l} , \dot{a}_m )^\bullet , p ) }\boldsymbol\mid{ l , m \in \omega \, \wedge \, p \in \mathbf{ P}_{ n + 1 } \, \wedge \, p^s_{ n + 1 } ( k ) ( l ) = m } \mathclose\} , \\ \dot{F}_n & = \mathopen \{{ \dot{f}_{ n , k } }\boldsymbol\mid{ k \in \omega } \mathclose\}^\bullet. \end{align*} $$
$$ \begin{align*} \dot{f}_{ n , k } &= \mathopen \{{ ( ( \check{l} , \dot{a}_m )^\bullet , p ) }\boldsymbol\mid{ l , m \in \omega \, \wedge \, p \in \mathbf{ P}_{ n + 1 } \, \wedge \, p^s_{ n + 1 } ( k ) ( l ) = m } \mathclose\} , \\ \dot{F}_n & = \mathopen \{{ \dot{f}_{ n , k } }\boldsymbol\mid{ k \in \omega } \mathclose\}^\bullet. \end{align*} $$
Note that these
![]() $\mathbf { P}$
-names are in
$\mathbf { P}$
-names are in
![]() $\mathsf {HS}$
. These, together with
$\mathsf {HS}$
. These, together with
![]() $\dot {A}$
and the
$\dot {A}$
and the
![]() $\dot {a}_n$
s, are the (hereditarily symmetric) names for all the generic sets we are interested in. Observe that
$\dot {a}_n$
s, are the (hereditarily symmetric) names for all the generic sets we are interested in. Observe that
![]() $\dot {f}_{ n , k }$
is a
$\dot {f}_{ n , k }$
is a
![]() $\mathbf { P}_{ n + 1 }$
-name for an R-chain belonging to
$\mathbf { P}_{ n + 1 }$
-name for an R-chain belonging to
![]() $\mathcal {N}_{ n + 1}$
, where R is the relation with
$\mathcal {N}_{ n + 1}$
, where R is the relation with
![]() $\mathbf { P}_{n+1}$
-name
$\mathbf { P}_{n+1}$
-name
![]() $\mathopen \{{ ( p^R_{ n + 1 } ( k ) , p ) }\boldsymbol \mid { p \in \mathbf { P}_{ n + 1 } } \mathclose \}$
.
$\mathopen \{{ ( p^R_{ n + 1 } ( k ) , p ) }\boldsymbol \mid { p \in \mathbf { P}_{ n + 1 } } \mathclose \}$
.
Fix a
![]() $\mathord {\mathrm {V}}$
-generic filter G for
$\mathord {\mathrm {V}}$
-generic filter G for
![]() $\mathbf { P}$
and, for all n, let
$\mathbf { P}$
and, for all n, let
![]() $\mathcal {N}_n$
be the symmetric extension obtained from
$\mathcal {N}_n$
be the symmetric extension obtained from
![]() $\mathopen \langle \mathbf { P} _n , \mathcal {G}_n , \mathcal {F}_n \mathclose \rangle $
, and
$\mathopen \langle \mathbf { P} _n , \mathcal {G}_n , \mathcal {F}_n \mathclose \rangle $
, and
![]() $\mathcal {N}$
be the symmetric extension, obtained from
$\mathcal {N}$
be the symmetric extension, obtained from
![]() $\mathopen \langle \mathbf { P} , \mathcal {G}, \mathcal {F} \mathclose \rangle $
. Clearly we have
$\mathopen \langle \mathbf { P} , \mathcal {G}, \mathcal {F} \mathclose \rangle $
. Clearly we have
For each
![]() $\mathbf { P}$
-name (e.g.,
$\mathbf { P}$
-name (e.g.,
![]() $\dot {A}$
), we let its symbol without the dot (i.e., A) be its evaluation according to G (i.e.,
$\dot {A}$
), we let its symbol without the dot (i.e., A) be its evaluation according to G (i.e.,
![]() $\dot {A}_G$
).
$\dot {A}_G$
).
Lemma 4.4. For every
![]() $n \in \omega $
, for every total and acyclic binary relation
$n \in \omega $
, for every total and acyclic binary relation
![]() $R \in \mathcal {N}_n$
on A, there is an an R-chain in
$R \in \mathcal {N}_n$
on A, there is an an R-chain in
![]() $\mathcal {N}_{n+1}$
.
$\mathcal {N}_{n+1}$
.
Proof Let
![]() $p \in G$
and
$p \in G$
and
![]() $\dot {R} \in \mathsf {HS} _n$
such that
$\dot {R} \in \mathsf {HS} _n$
such that
and without loss of generality we may assume that
![]() $p \in \mathbf { P} _n$
. We show that
$p \in \mathbf { P} _n$
. We show that
![]() $\dot {R}_G = \dot {S}_G$
for some
$\dot {R}_G = \dot {S}_G$
for some
![]() $\dot {S} \in \mathcal {R}_n$
as in (5). Let
$\dot {S} \in \mathcal {R}_n$
as in (5). Let
It readily follows that
![]() $\dot {S}$
is in
$\dot {S}$
is in
![]() $\mathcal {R}_n$
and
$\mathcal {R}_n$
and
![]() $p \Vdash \dot {R} = \dot {S}$
. Fix any
$p \Vdash \dot {R} = \dot {S}$
. Fix any
![]() $q \in \mathbf { P}_{n + 1}$
with
$q \in \mathbf { P}_{n + 1}$
with
![]() $q \le p$
. Pick an
$q \le p$
. Pick an
![]() $m \in \omega \setminus \operatorname {\mathrm {dom}} ( q_{ n + 1 } )$
and consider the finite sequence
$m \in \omega \setminus \operatorname {\mathrm {dom}} ( q_{ n + 1 } )$
and consider the finite sequence
![]() $q'$
such that
$q'$
such that
![]() $q^{\prime }_l = q_l$
for every
$q^{\prime }_l = q_l$
for every
![]() $l \neq n + 1$
and
$l \neq n + 1$
and
![]() $q^{\prime }_{ n + 1 } = q_{ n + 1 } \cup \mathopen \{ { ( m , ( \dot {S} , \emptyset ) ) } \mathclose \}$
. Then
$q^{\prime }_{ n + 1 } = q_{ n + 1 } \cup \mathopen \{ { ( m , ( \dot {S} , \emptyset ) ) } \mathclose \}$
. Then
![]() $q' \in \mathbf { P}_{ n + 1 }$
,
$q' \in \mathbf { P}_{ n + 1 }$
,
![]() $q' \le q$
and
$q' \le q$
and
By density,
Since
![]() $F_n \in \mathcal {N}_{ n + 1 }$
we are done.
$F_n \in \mathcal {N}_{ n + 1 }$
we are done.
Since A is not closed as a set of reals, there exists a total and acyclic binary relation over A in
![]() $\mathcal {N}_0$
(see Lemma 2.2). Therefore, by Lemma 4.4, the set A becomes Dedekind-infinite already in
$\mathcal {N}_0$
(see Lemma 2.2). Therefore, by Lemma 4.4, the set A becomes Dedekind-infinite already in
![]() $\mathcal {N}_1$
. However, the next proposition tells us that the range of any generic chain introduced by the iteration is far from being dense in A. This result is crucial in showing that A is not separable in
$\mathcal {N}_1$
. However, the next proposition tells us that the range of any generic chain introduced by the iteration is far from being dense in A. This result is crucial in showing that A is not separable in
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
In order to get to the key proposition, we need to recall the well-known notion of scattered space (e.g., see [Reference Semadeni11, Section 8.5]).
Definition 4.5. Given a topological space X, we let by ordinal induction
 $$ \begin{align*} X^{ ( 0 ) } &= X, \\ X^{ ( \alpha + 1 ) } &= \mathopen \{{ x \in X^{ ( \alpha ) } }\boldsymbol\mid{ x \text{ is a limit point of } X^{ ( \alpha ) } } \mathclose\}, \\ X^{ ( \lambda ) } &= \bigcap_{\alpha < \lambda} X^{ ( \alpha ) } \qquad \text{for }\lambda\text{ a limit ordinal}. \end{align*} $$
$$ \begin{align*} X^{ ( 0 ) } &= X, \\ X^{ ( \alpha + 1 ) } &= \mathopen \{{ x \in X^{ ( \alpha ) } }\boldsymbol\mid{ x \text{ is a limit point of } X^{ ( \alpha ) } } \mathclose\}, \\ X^{ ( \lambda ) } &= \bigcap_{\alpha < \lambda} X^{ ( \alpha ) } \qquad \text{for }\lambda\text{ a limit ordinal}. \end{align*} $$
For every space X there is necessarily an ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $X^{ ( \alpha ) } = X^{ ( \alpha + 1 ) }$
, and we call the least such ordinal the scattered height of the space. A topological space X is scattered if there is an
$X^{ ( \alpha ) } = X^{ ( \alpha + 1 ) }$
, and we call the least such ordinal the scattered height of the space. A topological space X is scattered if there is an
![]() $\alpha $
such that
$\alpha $
such that
![]() $X^{ ( \alpha ) } = \emptyset $
.
$X^{ ( \alpha ) } = \emptyset $
.
It is easy to check in
![]() $\mathsf {ZF}$
that every second countable scattered space is countable [Reference Semadeni11, Proposition 8.5.5]. If
$\mathsf {ZF}$
that every second countable scattered space is countable [Reference Semadeni11, Proposition 8.5.5]. If
![]() $\emptyset \neq X \subseteq \mathbb {R}$
is dense in itself, then
$\emptyset \neq X \subseteq \mathbb {R}$
is dense in itself, then
![]() $X^{( 1 )} = X$
and X is not scattered. In particular, A is not scattered.
$X^{( 1 )} = X$
and X is not scattered. In particular, A is not scattered.
For each
![]() $t \in {}^{<\omega } 2$
, we denote by
$t \in {}^{<\omega } 2$
, we denote by
![]() $\dot {{\boldsymbol N}\!}_t$
the canonical name for the basic open set
$\dot {{\boldsymbol N}\!}_t$
the canonical name for the basic open set
![]() ${\boldsymbol N}\!_{t}$
, i.e., the set of all infinite binary sequences extending t.
${\boldsymbol N}\!_{t}$
, i.e., the set of all infinite binary sequences extending t.
Proposition 4.6. For each
![]() $n , k \in \omega $
,
$n , k \in \omega $
,
![]() $\mathcal {N} \vDash \left ( \operatorname {\mathrm {Cl}}_A ( \operatorname {\mathrm {ran}} ( f_{ n , k } ) ) \right )^{ ( n + 2 ) } = \emptyset $
.
$\mathcal {N} \vDash \left ( \operatorname {\mathrm {Cl}}_A ( \operatorname {\mathrm {ran}} ( f_{ n , k } ) ) \right )^{ ( n + 2 ) } = \emptyset $
.
Proof In other words, we want to show that in
![]() $\mathcal {N}$
(or, equivalentlyFootnote
2
, in
$\mathcal {N}$
(or, equivalentlyFootnote
2
, in
![]() $\mathord {\mathrm {V}} [ G ]$
), for every
$\mathord {\mathrm {V}} [ G ]$
), for every
![]() $n , k$
, the closure with respect to A of the range of
$n , k$
, the closure with respect to A of the range of
![]() $f_{ n , k }$
is scattered of height at most
$f_{ n , k }$
is scattered of height at most
![]() $n + 2$
. For any
$n + 2$
. For any
![]() $H \subseteq \omega $
, let us introduce the
$H \subseteq \omega $
, let us introduce the
![]() $\mathbf { P}$
-name
$\mathbf { P}$
-name
Let
![]() $( \dagger )$
be the statement
$( \dagger )$
be the statement
![]() $\forall { n \in \omega } \, ( \dagger )_n$
, where
$\forall { n \in \omega } \, ( \dagger )_n$
, where
![]() $( \dagger )_n$
is the following statement: Let
$( \dagger )_n$
is the following statement: Let
![]() $k \in \omega $
,
$k \in \omega $
,
![]() $p = \mathopen \langle p_0, \dots p_n \mathclose \rangle \in \mathbf { P} _n$
,
$p = \mathopen \langle p_0, \dots p_n \mathclose \rangle \in \mathbf { P} _n$
,
![]() $\dot {R} \in \mathcal {R}_n$
with support
$\dot {R} \in \mathcal {R}_n$
with support
![]() $\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
such that
$\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
such that
![]() ${p \Vdash \dot {R}}$
is total and acyclic”. Assume also that, for each
${p \Vdash \dot {R}}$
is total and acyclic”. Assume also that, for each
![]() $i \leq n$
,
$i \leq n$
,
![]() $\operatorname {\mathrm {dom}} ( p_i ) = H_i$
, and, for all
$\operatorname {\mathrm {dom}} ( p_i ) = H_i$
, and, for all
![]() $0 < i \leq n$
, for all
$0 < i \leq n$
, for all
![]() $j \in H_i$
,
$j \in H_i$
,
![]() $\vec {H} {\mathop {\upharpoonright }} i$
is a support for
$\vec {H} {\mathop {\upharpoonright }} i$
is a support for
![]() $p_{i}^R ( j )$
. Then
$p_{i}^R ( j )$
. Then
 $$ \begin{align*} p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot{R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) ) \big )^{ ( 1 ) } \subseteq \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ). \end{align*} $$
$$ \begin{align*} p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot{R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) ) \big )^{ ( 1 ) } \subseteq \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ). \end{align*} $$
Remarks.
-
(a) The condition
 $p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R} , \emptyset ) ) } \mathclose \} \mathclose \rangle $
in the statement of
$p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R} , \emptyset ) ) } \mathclose \} \mathclose \rangle $
in the statement of
 $( \dagger )_n$
belongs to
$( \dagger )_n$
belongs to
 $\mathbf { P}_{ n + 1 }$
and it is obtained by extending p with the function with domain
$\mathbf { P}_{ n + 1 }$
and it is obtained by extending p with the function with domain
 $\mathopen \{ {k} \mathclose \} \subseteq \omega $
such that
$\mathopen \{ {k} \mathclose \} \subseteq \omega $
such that
 $k \mapsto ( \dot {R}, \emptyset ) \in \mathcal {R}_n \times {}^{ < \omega } \omega $
. It forces the limit points of
$k \mapsto ( \dot {R}, \emptyset ) \in \mathcal {R}_n \times {}^{ < \omega } \omega $
. It forces the limit points of
 $\operatorname {\mathrm {Cl}}_A ( \operatorname {\mathrm {ran}} ( f_{ n , k }) )$
to belong to the finite union
$\operatorname {\mathrm {Cl}}_A ( \operatorname {\mathrm {ran}} ( f_{ n , k }) )$
to belong to the finite union
 $A_{H_0} \cup \bigcup \mathopen \{{ \operatorname {\mathrm {ran}} ( f_{ i , j } ) }\boldsymbol \mid { i < n \text { and } j \in H_{ i + 1 }} \mathclose \}$
.
$A_{H_0} \cup \bigcup \mathopen \{{ \operatorname {\mathrm {ran}} ( f_{ i , j } ) }\boldsymbol \mid { i < n \text { and } j \in H_{ i + 1 }} \mathclose \}$
. -
(b) Note that
 $p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R} , \emptyset ) ) } \mathclose \} \mathclose \rangle $
is the
$p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R} , \emptyset ) ) } \mathclose \} \mathclose \rangle $
is the
 $\le $
-maximum among the conditions
$\le $
-maximum among the conditions
 $q \le p$
such that
$q \le p$
such that
 $q_{ n + 1 }^R ( k ) = \dot {R}$
. Therefore, for any fixed
$q_{ n + 1 }^R ( k ) = \dot {R}$
. Therefore, for any fixed
 $n , k$
, the set of conditions
$n , k$
, the set of conditions
 $p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle $
we are considering in
$p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle $
we are considering in
 $( \dagger )_n$
is pre-dense in
$( \dagger )_n$
is pre-dense in
 $\mathbf { P}_{ n + 1 }$
(and also in
$\mathbf { P}_{ n + 1 }$
(and also in
 $\mathbf { P}$
).
$\mathbf { P}$
).
Claim 4.6.1. Assume
![]() $( \dagger )$
. For each
$( \dagger )$
. For each
![]() $n , k \in \omega $
,
$n , k \in \omega $
,
![]() $\Vdash \big ( \operatorname {\mathrm {Cl}}_{\dot {A}} ( \operatorname {\mathrm {ran}} ( \dot {f}_{ n , k } ) ) \big )^{( n + 2 ) } = \emptyset $
.
$\Vdash \big ( \operatorname {\mathrm {Cl}}_{\dot {A}} ( \operatorname {\mathrm {ran}} ( \dot {f}_{ n , k } ) ) \big )^{( n + 2 ) } = \emptyset $
.
Proof We prove the claim by induction on n. Let
![]() $n = 0$
and fix
$n = 0$
and fix
![]() $k \in \omega $
,
$k \in \omega $
,
![]() $p \in \mathbf { P}_0$
,
$p \in \mathbf { P}_0$
,
![]() $\dot {R} \in \mathcal {R}_0$
,
$\dot {R} \in \mathcal {R}_0$
,
![]() $\vec {H} = \mathopen \langle H_0 \mathclose \rangle $
satisfying the hypotheses of
$\vec {H} = \mathopen \langle H_0 \mathclose \rangle $
satisfying the hypotheses of
![]() $( \dagger )_0$
. By
$( \dagger )_0$
. By
![]() $( \dagger )_0$
,
$( \dagger )_0$
,
Since
![]() $H_0$
is finite, we have that
$H_0$
is finite, we have that
![]() $\Vdash "\dot {A}_{H_0}$
is finite”, so our condition forces that
$\Vdash "\dot {A}_{H_0}$
is finite”, so our condition forces that
![]() $\operatorname {\mathrm {Cl}}_A ( \operatorname {\mathrm {ran}} f_{ n , k } )$
has scattered height
$\operatorname {\mathrm {Cl}}_A ( \operatorname {\mathrm {ran}} f_{ n , k } )$
has scattered height
![]() $\leq 2$
, that is,
$\leq 2$
, that is,
By density, the base case follows.
Now the induction step. Let
![]() $n> 0$
and fix
$n> 0$
and fix
![]() $k \in \omega $
,
$k \in \omega $
,
![]() $p \in \mathbf { P}_n$
,
$p \in \mathbf { P}_n$
,
![]() $\dot {R} \in \mathcal {R}_n$
,
$\dot {R} \in \mathcal {R}_n$
,
![]() $\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
satisfying the hypotheses of
$\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
satisfying the hypotheses of
![]() $( \dagger )_n$
. By
$( \dagger )_n$
. By
![]() $( \dagger )_n$
,
$( \dagger )_n$
,
 $$\begin{align*}p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot{R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) ) \big )^{ ( 1) } \subseteq \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } }} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ). \end{align*}$$
$$\begin{align*}p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot{R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) ) \big )^{ ( 1) } \subseteq \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } }} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ). \end{align*}$$
As the
![]() $H_i$
s are all finite,
$H_i$
s are all finite,
 $$\begin{align*}p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot{R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) ) \big )^{ ( n + 2 ) } \subseteq \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 }}}} \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) ) \big )^{ ( n + 1 ) }. \end{align*}$$
$$\begin{align*}p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot{R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) ) \big )^{ ( n + 2 ) } \subseteq \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 }}}} \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) ) \big )^{ ( n + 1 ) }. \end{align*}$$
By induction hypothesis, for all
![]() $i < n$
and all
$i < n$
and all
![]() $j \in H_{ i + 1 }$
$j \in H_{ i + 1 }$
and hence,
By density, the induction step follows.
The statement
![]() $( \dagger )$
is proved by induction on
$( \dagger )$
is proved by induction on
![]() $n \in \omega $
.
$n \in \omega $
.
Let
![]() $n = 0$
and fix
$n = 0$
and fix
![]() $k \in \omega $
,
$k \in \omega $
,
![]() $p \in \mathbf { P}_0$
,
$p \in \mathbf { P}_0$
,
![]() $\dot {R} \in \mathcal {R}_0$
,
$\dot {R} \in \mathcal {R}_0$
,
![]() $\vec {H} = \mathopen \langle H_0 \mathclose \rangle $
satisfying the hypotheses of
$\vec {H} = \mathopen \langle H_0 \mathclose \rangle $
satisfying the hypotheses of
![]() $( \dagger )_0$
.
$( \dagger )_0$
.
Claim 4.6.2.
![]() $p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \operatorname {\mathrm {ran}} ( \dot {f}_{ 0 , k } ) \setminus \dot {A}_{ H_0 } \text { is discrete.}$
$p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \operatorname {\mathrm {ran}} ( \dot {f}_{ 0 , k } ) \setminus \dot {A}_{ H_0 } \text { is discrete.}$
Proof Assume for a contradiction that there are
![]() $q \leq p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle $
and
$q \leq p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle $
and
![]() $l \in \omega $
such that
$l \in \omega $
such that
Without loss of generality suppose that
![]() $\operatorname {\mathrm {lh}} ( q_1^s ( k ) )> l + 1$
and let
$\operatorname {\mathrm {lh}} ( q_1^s ( k ) )> l + 1$
and let
![]() $m = q_1^s ( k ) ( l )$
,
$m = q_1^s ( k ) ( l )$
,
![]() $t = q_0 ( m )$
—in particular,
$t = q_0 ( m )$
—in particular,
![]() $m \notin H_0$
and
$m \notin H_0$
and
![]() $q \Vdash \dot {f}_{ 0 , k } ( l ) = \dot {a}_m \in \dot {{\boldsymbol N}\!}_t$
. From our assumption and from the fact that
$q \Vdash \dot {f}_{ 0 , k } ( l ) = \dot {a}_m \in \dot {{\boldsymbol N}\!}_t$
. From our assumption and from the fact that
![]() $H_0$
is a finite set, it follows that there must be a
$H_0$
is a finite set, it follows that there must be a
![]() $z \leq q$
and an
$z \leq q$
and an
![]() $h> l$
such that
$h> l$
such that
Assume without loss of generality
![]() $\operatorname {\mathrm {lh}} ( z_1^s ( k ) )> h$
and let
$\operatorname {\mathrm {lh}} ( z_1^s ( k ) )> h$
and let
![]() $m' = z_1^s ( k ) ( h )$
,
$m' = z_1^s ( k ) ( h )$
,
![]() $t' = z_0 ( m ' )$
—in particular,
$t' = z_0 ( m ' )$
—in particular,
![]() $m' \notin H_0$
,
$m' \notin H_0$
,
![]() $t' \supseteq t$
and
$t' \supseteq t$
and
![]() $z_0 \Vdash \dot {a}_m \mathrel {\dot {R}^+} \dot {a}_{m'}$
. Note that
$z_0 \Vdash \dot {a}_m \mathrel {\dot {R}^+} \dot {a}_{m'}$
. Note that
![]() $m' \neq m$
, as otherwise
$m' \neq m$
, as otherwise
![]() $z_0$
would force
$z_0$
would force
![]() $\dot {R}$
to have a cycle, which is a contradiction, as
$\dot {R}$
to have a cycle, which is a contradiction, as
![]() $z_0$
extends p and by hypothesis p forces
$z_0$
extends p and by hypothesis p forces
![]() $\dot {R}$
to be acyclic.
$\dot {R}$
to be acyclic.
Subclaim 4.6.2.1.
![]() $p' = z_0 {\mathop {\upharpoonright }} ( \omega \setminus \mathopen \{ { m } \mathclose \} ) \cup \mathopen \{ { ( m , t' ) } \mathclose \} \Vdash \dot {a}_{m} \mathrel {\dot {R}^+} \dot {a}_{m'}.$
$p' = z_0 {\mathop {\upharpoonright }} ( \omega \setminus \mathopen \{ { m } \mathclose \} ) \cup \mathopen \{ { ( m , t' ) } \mathclose \} \Vdash \dot {a}_{m} \mathrel {\dot {R}^+} \dot {a}_{m'}.$
A quick observation: since
![]() $z_0 \le q_0$
,
$z_0 \le q_0$
,
![]() $z_0 ( m )$
surely extends
$z_0 ( m )$
surely extends
![]() $t = q_0 ( m )$
, but a priori
$t = q_0 ( m )$
, but a priori
![]() $z_0 ( m )$
could be incompatible with
$z_0 ( m )$
could be incompatible with
![]() $t' = z_0 ( m' ) = p' ( m )$
, making
$t' = z_0 ( m' ) = p' ( m )$
, making
![]() $p'$
incompatible with
$p'$
incompatible with
![]() $ z_0$
. Thus, our subclaim needs some care.
$ z_0$
. Thus, our subclaim needs some care.
Proof of the Subclaim
Let
![]() $m_0 , m_1 , \dots , m_{ h - l } \in \omega $
be such that
$m_0 , m_1 , \dots , m_{ h - l } \in \omega $
be such that
![]() $m_i = z_1^s ( k ) ( l + i )$
for all
$m_i = z_1^s ( k ) ( l + i )$
for all
![]() $i \le h - l$
. Note that
$i \le h - l$
. Note that
![]() $m_0 = m = q_1^s ( k ) ( l )$
and
$m_0 = m = q_1^s ( k ) ( l )$
and
![]() $m_1 = q_1^s ( k ) ( l + 1 )$
, since
$m_1 = q_1^s ( k ) ( l + 1 )$
, since
![]() $z \le q$
. Moreover,
$z \le q$
. Moreover,
![]() $m_{ h - l } = m'$
, by definition of
$m_{ h - l } = m'$
, by definition of
![]() $m'$
. We can assume that the
$m'$
. We can assume that the
![]() $m_i$
s are all distinct, as otherwise
$m_i$
s are all distinct, as otherwise
![]() $z_0$
would force
$z_0$
would force
![]() $\dot {R}$
to have a cycle.
$\dot {R}$
to have a cycle.
Clearly
![]() $q_0 \Vdash \dot {a}_{m_0} \mathrel {\dot {R}} \dot {a}_{m_1}$
. By the Restriction Lemma,
$q_0 \Vdash \dot {a}_{m_0} \mathrel {\dot {R}} \dot {a}_{m_1}$
. By the Restriction Lemma,
![]() $q_0 {\mathop {\upharpoonright }} H_0 \cup \mathopen \{ { m_0 , m_1 } \mathclose \}$
forces the same.
$q_0 {\mathop {\upharpoonright }} H_0 \cup \mathopen \{ { m_0 , m_1 } \mathclose \}$
forces the same.
On the other hand,
![]() $z_0 \Vdash \dot {a}_{m_1} \mathrel {\dot {R}} \dot {a}_{m_{2}} \mathrel {\dot {R}} \dots \mathrel {\dot {R}} \dot {a}_{m_{ h - l }}$
. Again by the Restriction Lemma,
$z_0 \Vdash \dot {a}_{m_1} \mathrel {\dot {R}} \dot {a}_{m_{2}} \mathrel {\dot {R}} \dots \mathrel {\dot {R}} \dot {a}_{m_{ h - l }}$
. Again by the Restriction Lemma,
![]() $z_0 {\mathop {\upharpoonright }} H_0 \cup \mathopen \{ { m_1 , m_2 , \dots , m_{ h - l } } \mathclose \}$
forces the same.
$z_0 {\mathop {\upharpoonright }} H_0 \cup \mathopen \{ { m_1 , m_2 , \dots , m_{ h - l } } \mathclose \}$
forces the same.
The condition
![]() $p' = z_0 {\mathop {\upharpoonright }} ( \omega \setminus \mathopen \{ { m_0 } \mathclose \} ) \cup \mathopen \{ { ( m_0 , t' ) } \mathclose \}$
extends both
$p' = z_0 {\mathop {\upharpoonright }} ( \omega \setminus \mathopen \{ { m_0 } \mathclose \} ) \cup \mathopen \{ { ( m_0 , t' ) } \mathclose \}$
extends both
![]() $q_0 {\mathop {\upharpoonright }} H_0 \cup \mathopen \{ { m_0 , m_1 } \mathclose \}$
and
$q_0 {\mathop {\upharpoonright }} H_0 \cup \mathopen \{ { m_0 , m_1 } \mathclose \}$
and
![]() $z_0 {\mathop {\upharpoonright }} H_0 \cup \mathopen \{ { m_1 , m_2 , \dots , m_{ h - l } } \mathclose \}$
—here use the fact that
$z_0 {\mathop {\upharpoonright }} H_0 \cup \mathopen \{ { m_1 , m_2 , \dots , m_{ h - l } } \mathclose \}$
—here use the fact that
![]() $m_0 \notin H_0$
and that all the
$m_0 \notin H_0$
and that all the
![]() $m_i$
s are distinct. Hence
$m_i$
s are distinct. Hence
![]() $p'$
forces
$p'$
forces
![]() $\dot {a}_{m_0} \mathrel {\dot {R}} \dot {a}_{m_{1}} \mathrel {\dot {R}} \dot {a}_{m_{2}} \mathrel {\dot {R}} \dots \mathrel {\dot {R}} \dot {a}_{m_{h-l}}$
.
$\dot {a}_{m_0} \mathrel {\dot {R}} \dot {a}_{m_{1}} \mathrel {\dot {R}} \dot {a}_{m_{2}} \mathrel {\dot {R}} \dots \mathrel {\dot {R}} \dot {a}_{m_{h-l}}$
.
Let
![]() $\pi _0 \colon \omega \to \omega $
be the permutation that swaps m and
$\pi _0 \colon \omega \to \omega $
be the permutation that swaps m and
![]() $m'$
fixing everything else—in particular,
$m'$
fixing everything else—in particular,
![]() $\pi _0 \in \operatorname {\mathrm {Fix}} (H_0)$
and
$\pi _0 \in \operatorname {\mathrm {Fix}} (H_0)$
and
![]() $\pi _0 \dot {R} = \dot {R}$
. Then, by the Symmetry Lemma,
$\pi _0 \dot {R} = \dot {R}$
. Then, by the Symmetry Lemma,
but then
![]() $p'$
both extends p and forces
$p'$
both extends p and forces
![]() $\dot {a}_{m} \mathrel {\dot {R}^+} \dot {a}_m$
, which is a contradiction, since we assumed that p forces
$\dot {a}_{m} \mathrel {\dot {R}^+} \dot {a}_m$
, which is a contradiction, since we assumed that p forces
![]() $\dot {R}$
to be acyclic.
$\dot {R}$
to be acyclic.
By Claim 4.6.2, condition
![]() $p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle $
forces that the limit points of
$p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle $
forces that the limit points of
![]() $\operatorname {\mathrm {ran}} ( f_{ 0 , k } )$
belong to the finite set
$\operatorname {\mathrm {ran}} ( f_{ 0 , k } )$
belong to the finite set
![]() $A_{H_0 }$
. The next claim shows that the same is true for the larger set
$A_{H_0 }$
. The next claim shows that the same is true for the larger set
![]() $\operatorname {\mathrm {Cl}}_{A} ( \operatorname {\mathrm {ran}} ( f_{ 0 , k } ) )$
.
$\operatorname {\mathrm {Cl}}_{A} ( \operatorname {\mathrm {ran}} ( f_{ 0 , k } ) )$
.
Claim 4.6.3.
![]() $p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \big ( \operatorname {\mathrm {Cl}}_{\dot {A}} ( \operatorname {\mathrm {ran}} ( \dot {f}_{ 0 , k } ) ) \big )^{ ( 1 ) } \subseteq \dot {A}_{ H_0 }$
.
$p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \big ( \operatorname {\mathrm {Cl}}_{\dot {A}} ( \operatorname {\mathrm {ran}} ( \dot {f}_{ 0 , k } ) ) \big )^{ ( 1 ) } \subseteq \dot {A}_{ H_0 }$
.
Proof Suppose for a contradiction that the claim is false. Then there is a
![]() $q \leq p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle $
and an
$q \leq p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle $
and an
![]() $m \notin H_0$
such that
$m \notin H_0$
such that
Note that, since
![]() $H_0$
is finite, q actually forces
$H_0$
is finite, q actually forces
![]() $\dot {a}_m$
to be a limit point of
$\dot {a}_m$
to be a limit point of
![]() $\operatorname {\mathrm {ran}} ( \dot {f}_{ 0 , k } ) \setminus \dot {A}_{ H_0 }$
. Hence, it follows from Claim 4.6.2 that q forces
$\operatorname {\mathrm {ran}} ( \dot {f}_{ 0 , k } ) \setminus \dot {A}_{ H_0 }$
. Hence, it follows from Claim 4.6.2 that q forces
![]() $\dot {a}_m$
not to be in the range of
$\dot {a}_m$
not to be in the range of
![]() $\dot {f}_{ 0 , k }$
. In particular,
$\dot {f}_{ 0 , k }$
. In particular,
![]() $m \notin \operatorname {\mathrm {ran}} ( q_1^s ( k ) )$
.
$m \notin \operatorname {\mathrm {ran}} ( q_1^s ( k ) )$
.
The condition
![]() $q' = \mathopen \langle q_0, q_1 {\mathop {\upharpoonright }} \mathopen \{ { k } \mathclose \} \mathclose \rangle $
extends p and, by the Restriction Lemma, still forces (7). Let t be
$q' = \mathopen \langle q_0, q_1 {\mathop {\upharpoonright }} \mathopen \{ { k } \mathclose \} \mathclose \rangle $
extends p and, by the Restriction Lemma, still forces (7). Let t be
![]() $q_0 ( m )$
—in particular,
$q_0 ( m )$
—in particular,
![]() $q' \Vdash \dot {a}_m \in \dot {{\boldsymbol N}\!}_t$
.
$q' \Vdash \dot {a}_m \in \dot {{\boldsymbol N}\!}_t$
.
We now show
![]() $q' \Vdash \dot {{\boldsymbol N}\!}_t \subseteq \operatorname {\mathrm {Cl}} ( \operatorname {\mathrm {ran}} ( \dot {f}_{ 0 , k } ) \setminus \dot {A}_{H_0} )$
, which clearly contradicts Claim 4.6.2, as every discrete set of reals is nowhere dense. Pick any
$q' \Vdash \dot {{\boldsymbol N}\!}_t \subseteq \operatorname {\mathrm {Cl}} ( \operatorname {\mathrm {ran}} ( \dot {f}_{ 0 , k } ) \setminus \dot {A}_{H_0} )$
, which clearly contradicts Claim 4.6.2, as every discrete set of reals is nowhere dense. Pick any
![]() $z \leq q'$
and a
$z \leq q'$
and a
![]() $t'\supseteq t$
. Fix an
$t'\supseteq t$
. Fix an
![]() $m' \notin H_0 \cup \operatorname {\mathrm {dom}} ( z_0 ) \cup \operatorname {\mathrm {ran}} ( q_1^s ( k ) )$
. Define
$m' \notin H_0 \cup \operatorname {\mathrm {dom}} ( z_0 ) \cup \operatorname {\mathrm {ran}} ( q_1^s ( k ) )$
. Define
![]() $z'$
to be the condition such that
$z'$
to be the condition such that
![]() $z_0' = z_0 \cup \mathopen \{ { ( m' , t' ) } \mathclose \}$
and
$z_0' = z_0 \cup \mathopen \{ { ( m' , t' ) } \mathclose \}$
and
![]() $z_i' = z_i$
for every
$z_i' = z_i$
for every
![]() $i> 0$
.
$i> 0$
.
Now,
![]() $z'$
clearly extends z. Moreover, if we let
$z'$
clearly extends z. Moreover, if we let
![]() $\pi _0$
be the permutation of
$\pi _0$
be the permutation of
![]() $\omega $
that swaps m and
$\omega $
that swaps m and
![]() $m'$
,
$m'$
,
![]() $z'$
also extends
$z'$
also extends
![]() $\mathopen \langle \pi _0 \mathclose \rangle q'$
. Indeed, since
$\mathopen \langle \pi _0 \mathclose \rangle q'$
. Indeed, since
![]() $t' \supseteq t$
, it’s clear that
$t' \supseteq t$
, it’s clear that
![]() $z^{\prime }_0$
extends
$z^{\prime }_0$
extends
![]() $\pi _0 q_0$
. But since both m and
$\pi _0 q_0$
. But since both m and
![]() $m'$
do not belong to
$m'$
do not belong to
![]() $H_0 \cup \operatorname {\mathrm {ran}} ( q_1^s ( k ) )$
, we also have
$H_0 \cup \operatorname {\mathrm {ran}} ( q_1^s ( k ) )$
, we also have
![]() $( \mathopen \langle \pi _0 \mathclose \rangle q')_1 = q^{\prime }_1$
, and therefore
$( \mathopen \langle \pi _0 \mathclose \rangle q')_1 = q^{\prime }_1$
, and therefore
![]() $\mathopen \langle z^{\prime }_0, z^{\prime }_1 \mathclose \rangle = \mathopen \langle z^{\prime }_0, z_1 \mathclose \rangle $
extends
$\mathopen \langle z^{\prime }_0, z^{\prime }_1 \mathclose \rangle = \mathopen \langle z^{\prime }_0, z_1 \mathclose \rangle $
extends
![]() $\mathopen \langle \pi _0 \mathclose \rangle q' = \mathopen \langle \pi _0 q_0 , q^{\prime }_1 \mathclose \rangle $
. Overall,
$\mathopen \langle \pi _0 \mathclose \rangle q' = \mathopen \langle \pi _0 q_0 , q^{\prime }_1 \mathclose \rangle $
. Overall,
![]() $z'$
extends
$z'$
extends
![]() $\mathopen \langle \pi _0 \mathclose \rangle q'$
.
$\mathopen \langle \pi _0 \mathclose \rangle q'$
.
By (7) and the Symmetry Lemma,
Since
![]() $z'$
extends
$z'$
extends
![]() $\mathopen \langle \pi _0 \mathclose \rangle q'$
and
$\mathopen \langle \pi _0 \mathclose \rangle q'$
and
![]() $z' \Vdash \dot {a}_{m'} \in \dot {{\boldsymbol N}\!}_{t'}$
, we have
$z' \Vdash \dot {a}_{m'} \in \dot {{\boldsymbol N}\!}_{t'}$
, we have
By density,
This proves
![]() $( \dagger )_0$
.
$( \dagger )_0$
.
Here comes the induction step: fix an
![]() $n> 0$
and suppose
$n> 0$
and suppose
![]() $( \dagger )_i$
holds for every
$( \dagger )_i$
holds for every
![]() $i < n$
, towards proving
$i < n$
, towards proving
![]() $( \dagger )_n$
. Fix
$( \dagger )_n$
. Fix
![]() $k \in \omega $
,
$k \in \omega $
,
![]() $p \in \mathbf { P}_n$
,
$p \in \mathbf { P}_n$
,
![]() $\dot {R} \in \mathcal {R}_n$
,
$\dot {R} \in \mathcal {R}_n$
,
![]() $\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
satisfying the hypotheses of
$\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
satisfying the hypotheses of
![]() $( \dagger )_n$
. The next claim is the analogue of Claim 4.6.2.
$( \dagger )_n$
. The next claim is the analogue of Claim 4.6.2.
Claim 4.6.4.
 $$\begin{align*}p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot{R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k }) \setminus \Big ( \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 }}}} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j }) \Big ) \text{ is discrete}. \end{align*}$$
$$\begin{align*}p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot{R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k }) \setminus \Big ( \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 }}}} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j }) \Big ) \text{ is discrete}. \end{align*}$$
Proof Suppose for a contradiction that there are
![]() $q \leq \mathopen \langle p, \mathopen \{ { ( k , ( \dot {R} , \emptyset ) ) } \mathclose \} \mathclose \rangle $
and
$q \leq \mathopen \langle p, \mathopen \{ { ( k , ( \dot {R} , \emptyset ) ) } \mathclose \} \mathclose \rangle $
and
![]() $l \in \omega $
such that
$l \in \omega $
such that
 $$ \begin{align*} q \Vdash \dot{f}_{ n , k } ( l ) \notin \dot{A}_{H_0} \cup \smash[b]{\bigcup_{\substack{i < n \\ j \in H_{ i + 1 } } }} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j }) &\text{ and }\dot{f}_{ n , k } ( l ) \text{ is a limit point of } \\ &\quad\operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \Big ( \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } }}} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \Big ). \end{align*} $$
$$ \begin{align*} q \Vdash \dot{f}_{ n , k } ( l ) \notin \dot{A}_{H_0} \cup \smash[b]{\bigcup_{\substack{i < n \\ j \in H_{ i + 1 } } }} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j }) &\text{ and }\dot{f}_{ n , k } ( l ) \text{ is a limit point of } \\ &\quad\operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \Big ( \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } }}} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \Big ). \end{align*} $$
Suppose without loss of generality that
![]() $\operatorname {\mathrm {lh}} ( q_{ n + 1 } ^s ( k ) )> l + 1$
and let
$\operatorname {\mathrm {lh}} ( q_{ n + 1 } ^s ( k ) )> l + 1$
and let
![]() $m = q_{ n + 1 }^s ( k ) ( l )$
, and
$m = q_{ n + 1 }^s ( k ) ( l )$
, and
![]() $t = q_0 ( m )$
—in particular,
$t = q_0 ( m )$
—in particular,
![]() $q \Vdash \dot {f}_{ n , k } ( l ) = \dot {a}_m \in \dot {{\boldsymbol N}\!}_t$
. By assumption there must be a
$q \Vdash \dot {f}_{ n , k } ( l ) = \dot {a}_m \in \dot {{\boldsymbol N}\!}_t$
. By assumption there must be a
![]() $z \leq q$
and an
$z \leq q$
and an
![]() $h> l$
such that
$h> l$
such that
 $$\begin{align*}z \Vdash \dot{f}_{ n , k } ( h ) \in \dot{{\boldsymbol N}\!}_t \setminus \bigg ( \dot{A}_{ H_0 } \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{i + 1}}}} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \bigg). \end{align*}$$
$$\begin{align*}z \Vdash \dot{f}_{ n , k } ( h ) \in \dot{{\boldsymbol N}\!}_t \setminus \bigg ( \dot{A}_{ H_0 } \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{i + 1}}}} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \bigg). \end{align*}$$
Assume without loss of generality
![]() $\operatorname {\mathrm {lh}} ( z_{n + 1 }^s ( k ) )> h$
and let
$\operatorname {\mathrm {lh}} ( z_{n + 1 }^s ( k ) )> h$
and let
![]() $m' = z_{ n + 1 }^s ( k ) ( h )$
, and
$m' = z_{ n + 1 }^s ( k ) ( h )$
, and
![]() $t' = z_0 ( m ' )$
—in particular
$t' = z_0 ( m ' )$
—in particular
![]() $t' \supseteq t$
and
$t' \supseteq t$
and
![]() $z {\mathop {\upharpoonright }} n + 1 \Vdash \dot {a}_m \mathrel {\dot {R}^+ } \dot {a}_{m'}$
. Since
$z {\mathop {\upharpoonright }} n + 1 \Vdash \dot {a}_m \mathrel {\dot {R}^+ } \dot {a}_{m'}$
. Since
 $$\begin{align*}z \Vdash \dot{a}_m, \dot{a}_m' \notin \bigg ( \dot{A}_{H_0} \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{i + 1}}}} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \bigg), \end{align*}$$
$$\begin{align*}z \Vdash \dot{a}_m, \dot{a}_m' \notin \bigg ( \dot{A}_{H_0} \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{i + 1}}}} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \bigg), \end{align*}$$
then, in particular,
 $$ \begin{align} m,m' \notin H_0 \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{i + 1}}} } \operatorname{\mathrm{ran}} \big(z^s_{i+1}(j)\big). \end{align} $$
$$ \begin{align} m,m' \notin H_0 \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{i + 1}}} } \operatorname{\mathrm{ran}} \big(z^s_{i+1}(j)\big). \end{align} $$
Now let
By an argument analogous to the one used in the proof of Subclaim 4.6.2.1, we can show that
If we let
![]() $\pi _0 \colon \omega \to \omega $
be the permutation that swaps m and
$\pi _0 \colon \omega \to \omega $
be the permutation that swaps m and
![]() $m'$
, then
$m'$
, then
![]() $\mathopen \langle \pi _0 \mathclose \rangle p' = p'$
. Indeed, it directly follows from the definition of
$\mathopen \langle \pi _0 \mathclose \rangle p' = p'$
. Indeed, it directly follows from the definition of
![]() $p'$
that
$p'$
that
![]() $\pi _0 p^{\prime }_0 = p^{\prime }_0$
. Moreover, by (8), both m and
$\pi _0 p^{\prime }_0 = p^{\prime }_0$
. Moreover, by (8), both m and
![]() $m'$
do not belong to
$m'$
do not belong to
![]() $H_0$
, hence
$H_0$
, hence
![]() $\mathopen \langle \pi _0 \mathclose \rangle \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. As such,
$\mathopen \langle \pi _0 \mathclose \rangle \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. As such,
![]() $( \mathopen \langle \pi _0 \mathclose \rangle p' )_i^R = ( p' )_i^R$
for every
$( \mathopen \langle \pi _0 \mathclose \rangle p' )_i^R = ( p' )_i^R$
for every
![]() $1 \le i \le n$
. Again by (8), m and
$1 \le i \le n$
. Again by (8), m and
![]() $m'$
do not belong to the range of
$m'$
do not belong to the range of
![]() $( p' )_i ^s ( j )$
for any
$( p' )_i ^s ( j )$
for any
![]() $1 \le i \le n$
and
$1 \le i \le n$
and
![]() $j \in \operatorname {\mathrm {dom}} ( p^{\prime }_i ) = H_i$
, and therefore
$j \in \operatorname {\mathrm {dom}} ( p^{\prime }_i ) = H_i$
, and therefore
![]() $( \mathopen \langle \pi _0 \mathclose \rangle p' )_i ^s = ( p' )_i ^s$
for every
$( \mathopen \langle \pi _0 \mathclose \rangle p' )_i ^s = ( p' )_i ^s$
for every
![]() $1 \le i \le n$
. Overall,
$1 \le i \le n$
. Overall,
![]() $\mathopen \langle \pi _0 \mathclose \rangle p' = p'$
.
$\mathopen \langle \pi _0 \mathclose \rangle p' = p'$
.
Next note that
![]() $\mathopen \langle \pi _0 \mathclose \rangle \dot {R} = \dot {R}$
, as
$\mathopen \langle \pi _0 \mathclose \rangle \dot {R} = \dot {R}$
, as
![]() $\mathopen \langle \pi _0 \mathclose \rangle \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. By the Symmetry Lemma,
$\mathopen \langle \pi _0 \mathclose \rangle \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
. By the Symmetry Lemma,
but then
![]() $p'$
both extends p and forces
$p'$
both extends p and forces
![]() $\dot {a}_m \mathrel { \dot {R}^+ } \dot {a}_m$
, which is a contradiction, since we assumed that p forces
$\dot {a}_m \mathrel { \dot {R}^+ } \dot {a}_m$
, which is a contradiction, since we assumed that p forces
![]() $\dot {R}$
to be acyclic.
$\dot {R}$
to be acyclic.
Claim 4.6.5.
 $$\begin{align*}p\Vdash \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{i+1}}}} \operatorname{\mathrm{ran}} ( \dot{f}_{i,j}) \text{ is closed with respect to } \dot{A}. \end{align*}$$
$$\begin{align*}p\Vdash \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{i+1}}}} \operatorname{\mathrm{ran}} ( \dot{f}_{i,j}) \text{ is closed with respect to } \dot{A}. \end{align*}$$
Proof Fix
![]() $q \le p$
and m such that
$q \le p$
and m such that
 $$\begin{align*}q \Vdash \dot{a}_m \in \operatorname{\mathrm{Cl}}_{\dot{A}}\Big ( \dot{A}_{H_0} \cup \bigcup_{ \smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \Big ). \end{align*}$$
$$\begin{align*}q \Vdash \dot{a}_m \in \operatorname{\mathrm{Cl}}_{\dot{A}}\Big ( \dot{A}_{H_0} \cup \bigcup_{ \smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \Big ). \end{align*}$$
We would like to prove that there is a condition
![]() $z \le q$
such that
$z \le q$
such that
 $$\begin{align*}z \Vdash \dot{a}_m \in \dot{A}_{H_0} \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{ i + 1 }}} } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) , \end{align*}$$
$$\begin{align*}z \Vdash \dot{a}_m \in \dot{A}_{H_0} \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{ i + 1 }}} } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) , \end{align*}$$
so, to avoid trivialities, we assume
 $$\begin{align*}q \Vdash \dot{a}_m \in \Big ( \operatorname{\mathrm{Cl}}_{\dot{A}} \big ( \dot{A}_{H_0} \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \big ) \Big )^{ ( 1 ) }. \end{align*}$$
$$\begin{align*}q \Vdash \dot{a}_m \in \Big ( \operatorname{\mathrm{Cl}}_{\dot{A}} \big ( \dot{A}_{H_0} \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \big ) \Big )^{ ( 1 ) }. \end{align*}$$
As the
![]() $H_i$
s are finite, there exists a
$H_i$
s are finite, there exists a
![]() $z \le q$
, an
$z \le q$
, an
![]() $i < n$
and some
$i < n$
and some
![]() $j \in H_{ i + 1 }$
such that
$j \in H_{ i + 1 }$
such that
![]() $z \Vdash \dot {a}_m \in ( \operatorname {\mathrm {Cl}}_{\dot {A}} ( \operatorname {\mathrm {ran}} ( \dot {f}_{ i , j } ) ) )^{ ( 1 ) }$
. But then, by
$z \Vdash \dot {a}_m \in ( \operatorname {\mathrm {Cl}}_{\dot {A}} ( \operatorname {\mathrm {ran}} ( \dot {f}_{ i , j } ) ) )^{ ( 1 ) }$
. But then, by
![]() $( \dagger )_i$
(here we use our induction hypothesis),
$( \dagger )_i$
(here we use our induction hypothesis),
 $$\begin{align*}z \Vdash \dot{a}_m \in \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) ) \big )^{ ( 1 ) } \subseteq \dot{A}_{ H_0 } \cup \bigcup_{\smash[b]{\substack{l < i \\ h \in H_{ l + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ l , h } ). \end{align*}$$
$$\begin{align*}z \Vdash \dot{a}_m \in \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) ) \big )^{ ( 1 ) } \subseteq \dot{A}_{ H_0 } \cup \bigcup_{\smash[b]{\substack{l < i \\ h \in H_{ l + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ l , h } ). \end{align*}$$
By density, the claim follows.
The next claim is the analogue of Claim 4.6.3.
Claim 4.6.6.
 $$\begin{align*}p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot{R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) ) \big )^{ ( 1 ) } \subseteq \dot{A}_{H_0} \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ). \end{align*}$$
$$\begin{align*}p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot{R}, \emptyset ) ) } \mathclose \} \mathclose \rangle \Vdash \big ( \operatorname{\mathrm{Cl}}_{\dot{A}} ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) ) \big )^{ ( 1 ) } \subseteq \dot{A}_{H_0} \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ). \end{align*}$$
Proof Suppose for a contradiction that this is not the case, then there is a
![]() $q \leq p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle $
and an m such that
$q \leq p {}^\smallfrown \mathopen \langle \mathopen \{ { ( k , ( \dot {R}, \emptyset ) ) } \mathclose \} \mathclose \rangle $
and an m such that
 $$\begin{align*}q \Vdash \dot{a}_m \text{ is a limit point of } \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \text{ and } \dot{a}_m \notin \dot{A}_{ H_0 } \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{ i + 1 }}}} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ). \end{align*}$$
$$\begin{align*}q \Vdash \dot{a}_m \text{ is a limit point of } \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \text{ and } \dot{a}_m \notin \dot{A}_{ H_0 } \cup \bigcup_{\smash[b]{ \substack{i < n \\ j \in H_{ i + 1 }}}} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ). \end{align*}$$
From Claim 4.6.5 it follows that
 $$ \begin{align} q \Vdash \dot{a}_m \text{ is a limit point of } \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \Big ( \dot{A}_{ H_0 } \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \Big ). \end{align} $$
$$ \begin{align} q \Vdash \dot{a}_m \text{ is a limit point of } \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \Big ( \dot{A}_{ H_0 } \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \Big ). \end{align} $$
But then, by Claim 4.6.4, q also forces
![]() $\dot {a}_m$
not to be in the range of
$\dot {a}_m$
not to be in the range of
![]() $\dot {f}_{ n , k }$
. In particular,
$\dot {f}_{ n , k }$
. In particular,
 $$ \begin{align} m \notin H_0 \cup \operatorname{\mathrm{ran}} ( q_{ n + 1 }^s ( k ) ) \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( q_{ i + 1 }^s ( j ) ). \end{align} $$
$$ \begin{align} m \notin H_0 \cup \operatorname{\mathrm{ran}} ( q_{ n + 1 }^s ( k ) ) \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( q_{ i + 1 }^s ( j ) ). \end{align} $$
Let
Then
![]() $q'$
extends p and, by the Restriction Lemma, still forces (9). Let t be
$q'$
extends p and, by the Restriction Lemma, still forces (9). Let t be
![]() $q_0 ( m )$
—in particular
$q_0 ( m )$
—in particular
![]() $q' \Vdash \dot {a}_m \in \dot {{\boldsymbol N}\!}_t$
.
$q' \Vdash \dot {a}_m \in \dot {{\boldsymbol N}\!}_t$
.
We now show that
 $$\begin{align*}q' \Vdash \dot{{\boldsymbol N}\!}_t \subseteq \operatorname{\mathrm{Cl}} \Big ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \big ( \dot{A}_{H_0} \cup \bigcup_{\substack{i < n \\ j \in H_{ i + 1 } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \big ) \Big ) , \end{align*}$$
$$\begin{align*}q' \Vdash \dot{{\boldsymbol N}\!}_t \subseteq \operatorname{\mathrm{Cl}} \Big ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \big ( \dot{A}_{H_0} \cup \bigcup_{\substack{i < n \\ j \in H_{ i + 1 } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \big ) \Big ) , \end{align*}$$
which contradicts Claim 4.6.4. Pick any
![]() $z \leq q'$
and
$z \leq q'$
and
![]() $t'\supseteq t$
. Fix an
$t'\supseteq t$
. Fix an
![]() $m' \in \omega $
such that
$m' \in \omega $
such that
 $$ \begin{align} m' \notin H_0 \cup \operatorname{\mathrm{dom}} ( z_0 ) \cup \operatorname{\mathrm{ran}} ( q_{ n + 1 }^s ( k ) ) \cup \bigcup_{\substack{i < n \\ j \in H_{i + 1 } } } \operatorname{\mathrm{ran}} ( q_{ i + 1 }^s ( j ) ). \end{align} $$
$$ \begin{align} m' \notin H_0 \cup \operatorname{\mathrm{dom}} ( z_0 ) \cup \operatorname{\mathrm{ran}} ( q_{ n + 1 }^s ( k ) ) \cup \bigcup_{\substack{i < n \\ j \in H_{i + 1 } } } \operatorname{\mathrm{ran}} ( q_{ i + 1 }^s ( j ) ). \end{align} $$
Define
![]() $z'$
to be the condition such that
$z'$
to be the condition such that
![]() $z^{\prime }_0 = z_0 \cup \mathopen \{ { ( m' , t' ) } \mathclose \}$
and
$z^{\prime }_0 = z_0 \cup \mathopen \{ { ( m' , t' ) } \mathclose \}$
and
![]() $z_i' = z_i$
for all
$z_i' = z_i$
for all
![]() $i> 0$
. Now,
$i> 0$
. Now,
![]() $z'$
clearly extends z. Moreover, if we let
$z'$
clearly extends z. Moreover, if we let
![]() $\pi _0$
be the permutation of
$\pi _0$
be the permutation of
![]() $\omega $
that swaps m and
$\omega $
that swaps m and
![]() $m'$
,
$m'$
,
![]() $z'$
also extends
$z'$
also extends
![]() $\mathopen \langle \pi _0 \mathclose \rangle q'$
. Indeed, since
$\mathopen \langle \pi _0 \mathclose \rangle q'$
. Indeed, since
![]() $t' \supseteq t$
, it’s clear that
$t' \supseteq t$
, it’s clear that
![]() $z^{\prime }_0$
extends
$z^{\prime }_0$
extends
![]() $\pi _0 q_0$
. But from (10) and (11), it follows that
$\pi _0 q_0$
. But from (10) and (11), it follows that
![]() $( \mathopen \langle \pi _0 \mathclose \rangle q' )_i = q^{\prime }_i$
for every
$( \mathopen \langle \pi _0 \mathclose \rangle q' )_i = q^{\prime }_i$
for every
![]() $1 \le i \le n+1$
, and therefore
$1 \le i \le n+1$
, and therefore
![]() $z'$
extends
$z'$
extends
![]() $\mathopen \langle \pi _0 \mathclose \rangle q'$
.
$\mathopen \langle \pi _0 \mathclose \rangle q'$
.
By (9) and the Symmetry Lemma,
 $$\begin{align*}\mathopen \langle \pi_0 \mathclose \rangle q' \Vdash \dot{a}_{m'} \in \operatorname{\mathrm{Cl}} \Big ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \big ( \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \big ) \Big ). \end{align*}$$
$$\begin{align*}\mathopen \langle \pi_0 \mathclose \rangle q' \Vdash \dot{a}_{m'} \in \operatorname{\mathrm{Cl}} \Big ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \big ( \dot{A}_{H_0} \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \big ) \Big ). \end{align*}$$
Since
![]() $z'$
extends
$z'$
extends
![]() $\mathopen \langle \pi _0 \mathclose \rangle q'$
and
$\mathopen \langle \pi _0 \mathclose \rangle q'$
and
![]() $z' \Vdash \dot {a}_{m'} \in \dot {{\boldsymbol N}\!}_{t'}$
, we have
$z' \Vdash \dot {a}_{m'} \in \dot {{\boldsymbol N}\!}_{t'}$
, we have
 $$\begin{align*}z' \Vdash \dot{{\boldsymbol N}\!}_{t'} \cap \operatorname{\mathrm{Cl}} \Big ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \big ( \dot{A}_{ H_0 } \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \big ) \Big ) \neq \emptyset. \end{align*}$$
$$\begin{align*}z' \Vdash \dot{{\boldsymbol N}\!}_{t'} \cap \operatorname{\mathrm{Cl}} \Big ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \big ( \dot{A}_{ H_0 } \cup \bigcup_{\smash[b]{\substack{i < n \\ j \in H_{ i + 1 } } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \big ) \Big ) \neq \emptyset. \end{align*}$$
By density,
 $$\begin{align*}q' \Vdash \dot{{\boldsymbol N}\!}_t \subseteq \operatorname{\mathrm{Cl}} \Big ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \big ( \dot{A}_{ H_0 } \cup \bigcup_{\substack{i < n \\ j \in H_{ i + 1 } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \big ) \Big ).\\[-50pt] \end{align*}$$
$$\begin{align*}q' \Vdash \dot{{\boldsymbol N}\!}_t \subseteq \operatorname{\mathrm{Cl}} \Big ( \operatorname{\mathrm{ran}} ( \dot{f}_{ n , k } ) \setminus \big ( \dot{A}_{ H_0 } \cup \bigcup_{\substack{i < n \\ j \in H_{ i + 1 } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) \big ) \Big ).\\[-50pt] \end{align*}$$
This completes the proof of
![]() $( \dagger )_n$
, so by induction
$( \dagger )_n$
, so by induction
![]() $( \dagger )$
holds. By Claim 4.6.1, we are done.
$( \dagger )$
holds. By Claim 4.6.1, we are done.
In light of Proposition 4.6, we can prove that in
![]() $\mathcal {N}$
every separable subset of A is scattered with finite scattered height.
$\mathcal {N}$
every separable subset of A is scattered with finite scattered height.
Theorem 4.7. In the model
![]() $\mathcal {N}$
the following holds
$\mathcal {N}$
the following holds
![]() $:$
for every separable
$:$
for every separable
![]() $S \subseteq A$
there is an
$S \subseteq A$
there is an
![]() $n \in \omega $
such that
$n \in \omega $
such that
![]() $S^{ ( n ) } = \emptyset $
.
$S^{ ( n ) } = \emptyset $
.
Proof Let
![]() $S \in \mathcal {N}$
be a separable subset of A and fix in
$S \in \mathcal {N}$
be a separable subset of A and fix in
![]() $\mathcal {N}$
a function
$\mathcal {N}$
a function
![]() $f \colon \omega \to A$
such that
$f \colon \omega \to A$
such that
![]() $S \subseteq \operatorname {\mathrm {Cl}} ( \operatorname {\mathrm {ran}} ( f ) )$
. Then there must be a
$S \subseteq \operatorname {\mathrm {Cl}} ( \operatorname {\mathrm {ran}} ( f ) )$
. Then there must be a
![]() $p \in G$
such that
$p \in G$
such that
where
![]() $\dot {f} \in \mathsf {HS}$
is a symmetric name for f, with support
$\dot {f} \in \mathsf {HS}$
is a symmetric name for f, with support
![]() $\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
. We can assume without loss of generality that
$\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
. We can assume without loss of generality that
![]() $\operatorname {\mathrm {dom}} (p_i) = H_i$
for each i, and that for all
$\operatorname {\mathrm {dom}} (p_i) = H_i$
for each i, and that for all
![]() $i> 0$
, for all
$i> 0$
, for all
![]() $j \in H_i$
,
$j \in H_i$
,
![]() $\vec {H}{\mathop {\upharpoonright }} i$
is a support for
$\vec {H}{\mathop {\upharpoonright }} i$
is a support for
![]() $p_{i}^R ( j )$
. We claim that
$p_{i}^R ( j )$
. We claim that
 $$\begin{align*}p \Vdash \operatorname{\mathrm{ran}} ( \dot{f} ) \subseteq \dot{A}_{H_0} \cup \bigcup_{\substack{i < n \\ j \in H_{ i + 1 } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) , \end{align*}$$
$$\begin{align*}p \Vdash \operatorname{\mathrm{ran}} ( \dot{f} ) \subseteq \dot{A}_{H_0} \cup \bigcup_{\substack{i < n \\ j \in H_{ i + 1 } } } \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ) , \end{align*}$$
where
![]() $\dot {A}_{H_0}$
is the
$\dot {A}_{H_0}$
is the
![]() $\mathbf { P}$
-name as in (6). If we manage to do so, then Proposition 4.6 ensures that
$\mathbf { P}$
-name as in (6). If we manage to do so, then Proposition 4.6 ensures that
![]() $\operatorname {\mathrm {Cl}}_A ( \operatorname {\mathrm {ran}} ( f ) )$
is scattered of height
$\operatorname {\mathrm {Cl}}_A ( \operatorname {\mathrm {ran}} ( f ) )$
is scattered of height
![]() $\leq n + 2$
, and, a fortiori, that
$\leq n + 2$
, and, a fortiori, that
![]() $S^{( n + 2 )} = \emptyset $
, as required.
$S^{( n + 2 )} = \emptyset $
, as required.
Suppose that the claim is false, then there exist
![]() $q \leq p$
and
$q \leq p$
and
![]() $l , m \in \omega $
such that
$l , m \in \omega $
such that
 $$ \begin{align} q \Vdash \dot{f} ( l ) = \dot{a}_m \notin \dot{A}_{H_0} \cup\bigcup_{\smash[b]{\substack{i < n \\ j \in H_{i + 1 } } }} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ). \end{align} $$
$$ \begin{align} q \Vdash \dot{f} ( l ) = \dot{a}_m \notin \dot{A}_{H_0} \cup\bigcup_{\smash[b]{\substack{i < n \\ j \in H_{i + 1 } } }} \operatorname{\mathrm{ran}} ( \dot{f}_{ i , j } ). \end{align} $$
In particular,
 $$ \begin{align} m \notin H_0 \cup \bigcup_{\substack{i < n \\ j \in H_{i + 1 } } } \operatorname{\mathrm{ran}} ( q_{ i + 1 } ^s ( j ) ). \end{align} $$
$$ \begin{align} m \notin H_0 \cup \bigcup_{\substack{i < n \\ j \in H_{i + 1 } } } \operatorname{\mathrm{ran}} ( q_{ i + 1 } ^s ( j ) ). \end{align} $$
Let
![]() $q' = \mathopen \langle q_0, q_1 {\mathop {\upharpoonright }} H_1, \dots , q_n {\mathop {\upharpoonright }} H_n \mathclose \rangle $
. Then, by the Restriction Lemma,
$q' = \mathopen \langle q_0, q_1 {\mathop {\upharpoonright }} H_1, \dots , q_n {\mathop {\upharpoonright }} H_n \mathclose \rangle $
. Then, by the Restriction Lemma,
![]() $q'$
still forces (12).
$q'$
still forces (12).
Fix an
![]() $m' \in \omega $
such that
$m' \in \omega $
such that
 $$ \begin{align} m' \notin H_0 \cup \operatorname{\mathrm{dom}} ( q_0 ) \cup \bigcup_{\substack{i < n \\ j \in H_{i + 1 } } } \operatorname{\mathrm{ran}} (q_{ i + 1 } ^s ( j ) ). \end{align} $$
$$ \begin{align} m' \notin H_0 \cup \operatorname{\mathrm{dom}} ( q_0 ) \cup \bigcup_{\substack{i < n \\ j \in H_{i + 1 } } } \operatorname{\mathrm{ran}} (q_{ i + 1 } ^s ( j ) ). \end{align} $$
Let
![]() $\pi _0$
be the permutation of
$\pi _0$
be the permutation of
![]() $\omega $
that swaps m and
$\omega $
that swaps m and
![]() $m'$
, then
$m'$
, then
![]() $\mathopen \langle \pi _0 \mathclose \rangle q'$
and
$\mathopen \langle \pi _0 \mathclose \rangle q'$
and
![]() $q'$
are compatible. Indeed, since
$q'$
are compatible. Indeed, since
![]() $m' \notin \operatorname {\mathrm {dom}} (q_0')$
, then
$m' \notin \operatorname {\mathrm {dom}} (q_0')$
, then
![]() $q^{\prime }_0$
and
$q^{\prime }_0$
and
![]() $\pi _0 q^{\prime }_0$
are clearly compatible. Moreover, it follows from (13) and (14) that
$\pi _0 q^{\prime }_0$
are clearly compatible. Moreover, it follows from (13) and (14) that
![]() $( \mathopen \langle \pi _0 \mathclose \rangle q')_i = q^{\prime }_i$
for every
$( \mathopen \langle \pi _0 \mathclose \rangle q')_i = q^{\prime }_i$
for every
![]() $1 \le i \le n$
, and therefore
$1 \le i \le n$
, and therefore
![]() $\mathopen \langle \pi _0 \mathclose \rangle q'$
and
$\mathopen \langle \pi _0 \mathclose \rangle q'$
and
![]() $q'$
are compatible. By the Symmetry Lemma,
$q'$
are compatible. By the Symmetry Lemma,
So
![]() $q'$
and
$q'$
and
![]() $\mathopen \langle \pi _0 \mathclose \rangle q'$
, while being compatible, force
$\mathopen \langle \pi _0 \mathclose \rangle q'$
, while being compatible, force
![]() $\dot {f}$
to take different values at l, but they both extend p, which forces
$\dot {f}$
to take different values at l, but they both extend p, which forces
![]() $\dot {f}$
to be a function. Contradiction.
$\dot {f}$
to be a function. Contradiction.
Corollary 4.8.
![]() $\mathcal {N} \vDash \neg {\mathsf {AC}}_\omega ( A )$
.
$\mathcal {N} \vDash \neg {\mathsf {AC}}_\omega ( A )$
.
Proof Assume for a contradiction that
![]() ${\mathsf {AC}}_\omega ( A )$
holds, then A is certainly separable. By Theorem 4.7, A would be scattered. But A has no isolated points. Contradiction.
${\mathsf {AC}}_\omega ( A )$
holds, then A is certainly separable. By Theorem 4.7, A would be scattered. But A has no isolated points. Contradiction.
Now we are left to prove that
![]() $\mathsf {DC} ( A )$
holds in
$\mathsf {DC} ( A )$
holds in
![]() $\mathcal {N}$
. Let
$\mathcal {N}$
. Let
![]() $\dot {\mathcal {N}}_n$
be the canonical name for the intermediate model
$\dot {\mathcal {N}}_n$
be the canonical name for the intermediate model
![]() $\mathcal {N}_n$
.
$\mathcal {N}_n$
.
Lemma 4.9. Let
![]() $n \in \omega $
and
$n \in \omega $
and
![]() $\dot {x} \in \mathsf {HS}$
with support
$\dot {x} \in \mathsf {HS}$
with support
![]() $\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
, then
$\vec {H} = \mathopen \langle H_0, \dots , H_n \mathclose \rangle $
, then
Proof Fix
![]() $( \dot {y} , p ) \in \dot {x}$
. As the set of q such that either
$( \dot {y} , p ) \in \dot {x}$
. As the set of q such that either
![]() $q \Vdash \dot {y} \in \dot { \mathcal {N}}_n$
or else
$q \Vdash \dot {y} \in \dot { \mathcal {N}}_n$
or else
![]() $q \Vdash \dot {y} \notin \dot { \mathcal {N}}_n$
is dense below p, there is a maximal antichain
$q \Vdash \dot {y} \notin \dot { \mathcal {N}}_n$
is dense below p, there is a maximal antichain
![]() $D_{ ( \dot {y} , p ) }$
below
$D_{ ( \dot {y} , p ) }$
below
![]() $ p$
and a map
$ p$
and a map
![]() $h_{ ( \dot {y} , p ) } \colon D_{ ( \dot {y} , p ) } \to \mathsf {HS} _n$
such that, for each
$h_{ ( \dot {y} , p ) } \colon D_{ ( \dot {y} , p ) } \to \mathsf {HS} _n$
such that, for each
![]() $q \in D_{ ( \dot {y} , p ) }$
, either
$q \in D_{ ( \dot {y} , p ) }$
, either
![]() $q \Vdash \dot {y} = h_{ ( \dot {y} , p ) } ( q )$
or
$q \Vdash \dot {y} = h_{ ( \dot {y} , p ) } ( q )$
or
![]() $q \Vdash \dot {y} \notin \dot {\mathcal {N}}_n$
. Let
$q \Vdash \dot {y} \notin \dot {\mathcal {N}}_n$
. Let
![]() $D^{\prime }_{ ( \dot {y} , p ) } = \mathopen \{{ q \in D_{ ( \dot {y} , p ) } }\boldsymbol \mid { q \Vdash \dot {y} \in \dot {\mathcal {N}}_n } \mathclose \}$
and let
$D^{\prime }_{ ( \dot {y} , p ) } = \mathopen \{{ q \in D_{ ( \dot {y} , p ) } }\boldsymbol \mid { q \Vdash \dot {y} \in \dot {\mathcal {N}}_n } \mathclose \}$
and let
Consider the following
![]() $\mathbf { P} _n$
-name:
$\mathbf { P} _n$
-name:
Claim 4.9.1.
![]() $\dot {w} \in \mathsf {HS} _n$
with support
$\dot {w} \in \mathsf {HS} _n$
with support
![]() $\vec {H}$
.
$\vec {H}$
.
Proof Let
![]() $\vec {\pi } \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
and
$\vec {\pi } \in \operatorname {\mathrm {Fix}} ( \vec {H} )$
and
![]() $( \dot {y} , q ) \in \dot {w}$
. By definition,
$( \dot {y} , q ) \in \dot {w}$
. By definition,
![]() $q \Vdash \dot {y} \in \dot {x}$
, hence
$q \Vdash \dot {y} \in \dot {x}$
, hence
![]() $\vec {\pi } q \Vdash \vec {\pi } \dot {y} \in \dot {x}$
. Since
$\vec {\pi } q \Vdash \vec {\pi } \dot {y} \in \dot {x}$
. Since
![]() $\vec {\pi } \dot {y} \in C$
, this means that
$\vec {\pi } \dot {y} \in C$
, this means that
![]() $( \vec {\pi } \dot {y}, \vec {\pi } q ) \in \dot {w}$
. Hence
$( \vec {\pi } \dot {y}, \vec {\pi } q ) \in \dot {w}$
. Hence
![]() $\vec {\pi } \dot {w} = \dot {w}$
.
$\vec {\pi } \dot {w} = \dot {w}$
.
Fix
![]() $p \in \mathbf { P}$
such that
$p \in \mathbf { P}$
such that
![]() $p \Vdash \dot {x} \subseteq \dot {\mathcal {N}}_n$
.
$p \Vdash \dot {x} \subseteq \dot {\mathcal {N}}_n$
.
Claim 4.9.2.
![]() $p \Vdash \dot {w} = \dot {x}$
.
$p \Vdash \dot {w} = \dot {x}$
.
Proof Let
![]() $q \leq p$
and
$q \leq p$
and
![]() $\dot {z} \in \mathsf {HS}$
such that
$\dot {z} \in \mathsf {HS}$
such that
![]() $q \Vdash \dot {z} \in \dot {x}$
. By definition of C and our hypothesis on p, there is an
$q \Vdash \dot {z} \in \dot {x}$
. By definition of C and our hypothesis on p, there is an
![]() $r \leq q$
and a
$r \leq q$
and a
![]() $\dot {y} \in C$
such that
$\dot {y} \in C$
such that
![]() $r \Vdash \dot {z} = \dot {y} \in \dot {x}$
. By the Restriction Lemma,
$r \Vdash \dot {z} = \dot {y} \in \dot {x}$
. By the Restriction Lemma,
![]() $r {\mathop {\upharpoonright }} n + 1 \Vdash \dot {y} \in \dot {x}$
, hence
$r {\mathop {\upharpoonright }} n + 1 \Vdash \dot {y} \in \dot {x}$
, hence
![]() $( \dot {y} , r {\mathop {\upharpoonright }} n + 1 ) \in \dot {w}$
and, in particular,
$( \dot {y} , r {\mathop {\upharpoonright }} n + 1 ) \in \dot {w}$
and, in particular,
![]() $r \Vdash \dot {z} = \dot {y} \in \dot {w}$
. By density,
$r \Vdash \dot {z} = \dot {y} \in \dot {w}$
. By density,
![]() $p \Vdash \dot {x} \subseteq \dot {w}$
.
$p \Vdash \dot {x} \subseteq \dot {w}$
.
The other inclusion is immediate from the definition of
![]() $\dot {w}$
.
$\dot {w}$
.
Therefore
![]() $p \Vdash \dot {x} \in \dot {\mathcal {N}}_n$
. By density,
$p \Vdash \dot {x} \in \dot {\mathcal {N}}_n$
. By density,
![]() $\Vdash \dot {x} \subseteq \dot {\mathcal {N}}_n \Rightarrow \dot {x} \in \dot { \mathcal {N} }_n$
.
$\Vdash \dot {x} \subseteq \dot {\mathcal {N}}_n \Rightarrow \dot {x} \in \dot { \mathcal {N} }_n$
.
Theorem 4.10.
![]() $\mathcal {N} \vDash \mathsf {DC} ( A )$
.
$\mathcal {N} \vDash \mathsf {DC} ( A )$
.
Proof Since every binary relation
![]() $R \in \mathcal {N}$
on A is a subset of
$R \in \mathcal {N}$
on A is a subset of
![]() $A\times A \in \mathcal {N}_0$
, it follows from Lemma 4.9 that
$A\times A \in \mathcal {N}_0$
, it follows from Lemma 4.9 that
![]() $R \in \mathcal {N}_n$
for some n. Now, either R is cyclic, but then it surely has a chain, or it is acyclic, but then Lemma 4.4 says that in
$R \in \mathcal {N}_n$
for some n. Now, either R is cyclic, but then it surely has a chain, or it is acyclic, but then Lemma 4.4 says that in
![]() $\mathcal {N}_{n+1} \subseteq \mathcal {N}$
there is a chain for this relation.
$\mathcal {N}_{n+1} \subseteq \mathcal {N}$
there is a chain for this relation.
This finishes the proof of Theorem 4.1.
5 Some complementary results
We collect some facts related to our main results, and conclude with some open questions.
5.1 Dependent choice propagates under finite unions
By Proposition 2.1, the axiom
![]() $\mathsf {DC} (X)$
is closed under surjective images and, hence, under subsets. The next result shows that it is also closed under finite unions.
$\mathsf {DC} (X)$
is closed under surjective images and, hence, under subsets. The next result shows that it is also closed under finite unions.
Theorem 5.1.
![]() $\mathsf {DC} ( X ) \wedge \mathsf {DC} ( Y ) \Rightarrow \mathsf {DC} ( X \cup Y )$
.
$\mathsf {DC} ( X ) \wedge \mathsf {DC} ( Y ) \Rightarrow \mathsf {DC} ( X \cup Y )$
.
Corollary 5.2.
![]() $\mathsf {DC} ( X ) \Rightarrow \mathsf {DC} ( X \times n )$
, for all sets X and all
$\mathsf {DC} ( X ) \Rightarrow \mathsf {DC} ( X \times n )$
, for all sets X and all
![]() $n \in \omega $
.
$n \in \omega $
.
The natural progression from Corollary 5.2 would be to prove that
![]() $\mathsf {DC} ( X ) \Rightarrow \mathsf {DC} ( X \times \omega )$
, but this cannot be established in
$\mathsf {DC} ( X ) \Rightarrow \mathsf {DC} ( X \times \omega )$
, but this cannot be established in
![]() $\mathsf {ZF}$
, since
$\mathsf {ZF}$
, since
![]() $\mathsf {DC} ( X \times \omega )$
implies
$\mathsf {DC} ( X \times \omega )$
implies
![]() ${\mathsf {AC}}_\omega ( X )$
(part (d) of Proposition 2.1) and we know from Theorem 4.1 that
${\mathsf {AC}}_\omega ( X )$
(part (d) of Proposition 2.1) and we know from Theorem 4.1 that
![]() $\mathsf {DC} ( X )$
does not necessarily imply
$\mathsf {DC} ( X )$
does not necessarily imply
![]() ${\mathsf {AC}}_\omega ( X )$
.
${\mathsf {AC}}_\omega ( X )$
.
If a binary relation R is such that
![]() $\operatorname {\mathrm {ran}} ( R ) \subseteq \operatorname {\mathrm {dom}} ( R )$
, then it is total on its domain. The largest
$\operatorname {\mathrm {ran}} ( R ) \subseteq \operatorname {\mathrm {dom}} ( R )$
, then it is total on its domain. The largest
![]() $R' \subseteq R$
such that
$R' \subseteq R$
such that
![]() $\operatorname {\mathrm {ran}} ( R' ) \subseteq \operatorname {\mathrm {dom}} ( R' )$
is
$\operatorname {\mathrm {ran}} ( R' ) \subseteq \operatorname {\mathrm {dom}} ( R' )$
is
By part (a) of Proposition 2.1 it is easy to see that
Proof of Theorem 5.1
Suppose
![]() $\mathsf {DC} ( X )$
and
$\mathsf {DC} ( X )$
and
![]() $\mathsf {DC} ( Y )$
, and let
$\mathsf {DC} ( Y )$
, and let
![]() $R \subseteq ( X \cup Y )^2$
be total, towards proving that there is an R-chain. Without loss of generality, we may assume that X and Y are nonempty and disjoint. If
$R \subseteq ( X \cup Y )^2$
be total, towards proving that there is an R-chain. Without loss of generality, we may assume that X and Y are nonempty and disjoint. If
![]() $\mathcal {D} ( R {\mathop {\upharpoonright }} X ) \neq \emptyset $
, then by
$\mathcal {D} ( R {\mathop {\upharpoonright }} X ) \neq \emptyset $
, then by
![]() $\mathsf {DC} ( X )$
and (15) there is a
$\mathsf {DC} ( X )$
and (15) there is a
![]() $\mathcal {D} ( R {\mathop {\upharpoonright }} X )$
-chain, which is, in particular an R-chain. Similarly, if
$\mathcal {D} ( R {\mathop {\upharpoonright }} X )$
-chain, which is, in particular an R-chain. Similarly, if
![]() $\mathcal {D} ( R {\mathop {\upharpoonright }} Y ) \neq \emptyset $
, then there is an R-chain. Therefore, without loss of generality, we may assume that R is acyclic, and that
$\mathcal {D} ( R {\mathop {\upharpoonright }} Y ) \neq \emptyset $
, then there is an R-chain. Therefore, without loss of generality, we may assume that R is acyclic, and that
Recall that
![]() $R^+$
is the smallest transitive relation containing R. If
$R^+$
is the smallest transitive relation containing R. If
![]() $x \in X \cup Y$
and
$x \in X \cup Y$
and
![]() $R^+ ( x ) \subseteq X$
, then
$R^+ ( x ) \subseteq X$
, then
![]() $R {\mathop {\upharpoonright }} R^+ ( x )$
would witness that
$R {\mathop {\upharpoonright }} R^+ ( x )$
would witness that
![]() $\mathcal {D} ( R {\mathop {\upharpoonright }} X ) \neq \emptyset $
, against (16). Similarly
$\mathcal {D} ( R {\mathop {\upharpoonright }} X ) \neq \emptyset $
, against (16). Similarly
![]() $R^+ ( x )$
cannot be included in Y. Therefore
$R^+ ( x )$
cannot be included in Y. Therefore
Here is the idea of the proof. By (16), any R-chain
![]() $( z_n )_{ n \in \omega }$
must visit both X and Y infinitely often, so
$( z_n )_{ n \in \omega }$
must visit both X and Y infinitely often, so
![]() $( z_n )_{ n \in \omega }$
can be seen as the careful merging of two sequences
$( z_n )_{ n \in \omega }$
can be seen as the careful merging of two sequences
![]() $( x_n )_{ n \in \omega }$
in X and
$( x_n )_{ n \in \omega }$
in X and
![]() $( y_n )_{ n \in \omega }$
in Y. The sequence
$( y_n )_{ n \in \omega }$
in Y. The sequence
![]() $( x_n )_{ n \in \omega }$
is obtained by applying
$( x_n )_{ n \in \omega }$
is obtained by applying
![]() $\mathsf {DC} ( X )$
to a total relation
$\mathsf {DC} ( X )$
to a total relation
![]() $R_X$
on X such that
$R_X$
on X such that
![]() $R {\mathop {\upharpoonright }} X \subseteq R_X \subseteq R^+$
. Using
$R {\mathop {\upharpoonright }} X \subseteq R_X \subseteq R^+$
. Using
![]() $( x_n )_{ n \in \omega }$
, a suitable total relation
$( x_n )_{ n \in \omega }$
, a suitable total relation
![]() $R_Y$
on some
$R_Y$
on some
![]() $Y' \subseteq Y$
is defined, and by
$Y' \subseteq Y$
is defined, and by
![]() $\mathsf {DC} ( Y )$
the required sequence
$\mathsf {DC} ( Y )$
the required sequence
![]() $( y_n )_{ n \in \omega }$
is obtained. Here come the details.
$( y_n )_{ n \in \omega }$
is obtained. Here come the details.
Let
![]() $R_X$
be the relation on X given by
$R_X$
be the relation on X given by
![]() $R {\mathop {\upharpoonright }} X$
, together with all pairs
$R {\mathop {\upharpoonright }} X$
, together with all pairs
![]() $( x , x' )$
such that
$( x , x' )$
such that
![]() $x \mathrel {R} y_0 \mathrel {R} y_1 \mathrel {R} \dots \mathrel {R} y_n \mathrel {R} x'$
for some finite sequence of elements of Y:
$x \mathrel {R} y_0 \mathrel {R} y_1 \mathrel {R} \dots \mathrel {R} y_n \mathrel {R} x'$
for some finite sequence of elements of Y:
 $$ \begin{align*} R_X = ( R {\mathop{\upharpoonright}} X ) \cup &\{ ( x , x' ) \in X^2 \boldsymbol\mid \exists {m \geq 1 } \, \exists {s \in {}^{m } Y} \, \\ &( x \mathrel{R} s ( 0 ) \wedge s ( m - 1 ) \mathrel{R} x' \wedge \forall {i < m - 1 } \, ( s ( i ) \mathrel{R} s ( i + 1 ) ) ) \}. \end{align*} $$
$$ \begin{align*} R_X = ( R {\mathop{\upharpoonright}} X ) \cup &\{ ( x , x' ) \in X^2 \boldsymbol\mid \exists {m \geq 1 } \, \exists {s \in {}^{m } Y} \, \\ &( x \mathrel{R} s ( 0 ) \wedge s ( m - 1 ) \mathrel{R} x' \wedge \forall {i < m - 1 } \, ( s ( i ) \mathrel{R} s ( i + 1 ) ) ) \}. \end{align*} $$
It is immediate that
![]() $R_X \subseteq R^+$
.
$R_X \subseteq R^+$
.
Claim 5.2.1.
![]() $R_X$
is total on X.
$R_X$
is total on X.
Proof We must show that
![]() $\operatorname {\mathrm {dom}} ( R_X ) = X$
. Let
$\operatorname {\mathrm {dom}} ( R_X ) = X$
. Let
![]() $x \in X$
. If
$x \in X$
. If
![]() $R ( x ) \cap X \neq \emptyset $
, then
$R ( x ) \cap X \neq \emptyset $
, then
![]() $x \in \operatorname {\mathrm {dom}} ( R {\mathop {\upharpoonright }} X) \subseteq \operatorname {\mathrm {dom}} (R_X)$
.
$x \in \operatorname {\mathrm {dom}} ( R {\mathop {\upharpoonright }} X) \subseteq \operatorname {\mathrm {dom}} (R_X)$
.
Now suppose otherwise. By (3)
![]() $R^+ ( x ) \nsubseteq Y$
, so there are
$R^+ ( x ) \nsubseteq Y$
, so there are
![]() $y_0 , \dots , y_n \in Y$
and
$y_0 , \dots , y_n \in Y$
and
![]() $x' \in X$
such that
$x' \in X$
such that
![]() $x \mathrel {R} y_0 \mathrel {R} \dots \mathrel {R} y_n \mathrel {R} x'$
. Thus
$x \mathrel {R} y_0 \mathrel {R} \dots \mathrel {R} y_n \mathrel {R} x'$
. Thus
![]() $( x , x' ) \in R_X$
, so
$( x , x' ) \in R_X$
, so
![]() $x \in \operatorname {\mathrm {dom}} ( R_X )$
.
$x \in \operatorname {\mathrm {dom}} ( R_X )$
.
By
![]() $\mathsf {DC} ( X )$
there is an
$\mathsf {DC} ( X )$
there is an
![]() $R_X$
-chain
$R_X$
-chain
![]() $( x_n )_{ n \in \omega }$
.
$( x_n )_{ n \in \omega }$
.
Claim 5.2.2.
![]() $\forall {n} \, \exists { m> n } \, \neg ( x_{m} \mathrel {R} x_{m+1} )$
.
$\forall {n} \, \exists { m> n } \, \neg ( x_{m} \mathrel {R} x_{m+1} )$
.
Proof Towards a contradiction, suppose that there is
![]() $\bar {n}\in \omega $
such that
$\bar {n}\in \omega $
such that
![]() $x_{m} \mathrel {R} x_{ m + 1 }$
for every
$x_{m} \mathrel {R} x_{ m + 1 }$
for every
![]() $m \geq \bar {n}$
. Then
$m \geq \bar {n}$
. Then
![]() $R {\mathop {\upharpoonright }} \mathopen \{{ x_m}\boldsymbol \mid { m \geq \bar {n}} \mathclose \}$
is total on
$R {\mathop {\upharpoonright }} \mathopen \{{ x_m}\boldsymbol \mid { m \geq \bar {n}} \mathclose \}$
is total on
![]() $\mathopen \{{ x_m}\boldsymbol \mid { m \geq \bar {n}} \mathclose \}$
and contained in
$\mathopen \{{ x_m}\boldsymbol \mid { m \geq \bar {n}} \mathclose \}$
and contained in
![]() $R {\mathop {\upharpoonright }} X$
, against (16).
$R {\mathop {\upharpoonright }} X$
, against (16).
Let
![]() $( n_k )_{ k \in \omega }$
be the sequence enumerating the set of ms such that
$( n_k )_{ k \in \omega }$
be the sequence enumerating the set of ms such that
![]() $\neg ( x_{m} \mathrel {R} x_{ m + 1 } )$
. By the definition of
$\neg ( x_{m} \mathrel {R} x_{ m + 1 } )$
. By the definition of
![]() $R_X$
, each
$R_X$
, each
![]() $x_{n_k}$
is linked to
$x_{n_k}$
is linked to
![]() $x_{ n_k + 1}$
via R through some finite path in Y, and let
$x_{ n_k + 1}$
via R through some finite path in Y, and let
![]() $Y_k$
be the collection of all places visited by these paths:
$Y_k$
be the collection of all places visited by these paths:
 $$ \begin{align*} Y_k \mathrel{{:}{=}} \bigcup \big \{ \operatorname{\mathrm{ran}} ( s ) \boldsymbol\mid \exists {m } \, \big ( s \in {}^{m+ 1} Y \wedge x_{n_k} \mathrel{R} s ( 0 ) \wedge &s ( m ) \mathrel{R} x_{ n_k + 1 } \wedge{} \\ &\forall {i < m } \, ( s ( i ) \mathrel{R} s ( i + 1 ) ) \big ) \big \}. \end{align*} $$
$$ \begin{align*} Y_k \mathrel{{:}{=}} \bigcup \big \{ \operatorname{\mathrm{ran}} ( s ) \boldsymbol\mid \exists {m } \, \big ( s \in {}^{m+ 1} Y \wedge x_{n_k} \mathrel{R} s ( 0 ) \wedge &s ( m ) \mathrel{R} x_{ n_k + 1 } \wedge{} \\ &\forall {i < m } \, ( s ( i ) \mathrel{R} s ( i + 1 ) ) \big ) \big \}. \end{align*} $$
Claim 5.2.3. The
![]() $Y_k$
s are nonempty, pairwise disjoint subsets of Y.
$Y_k$
s are nonempty, pairwise disjoint subsets of Y.
Proof For each k we have
![]() $( x_{ n_k } , x_{ n_k + 1 } ) \in R_X \setminus R$
. This means that there is some
$( x_{ n_k } , x_{ n_k + 1 } ) \in R_X \setminus R$
. This means that there is some
![]() $\mathopen \langle y_0 , \dots , y_m \mathclose \rangle \in {}^{<\omega } Y$
such that
$\mathopen \langle y_0 , \dots , y_m \mathclose \rangle \in {}^{<\omega } Y$
such that
![]() $x_{n_k} \mathrel {R} y_0 \mathrel {R} \dots \mathrel {R} y_m \mathrel {R} x_{n_k + 1 }$
. In particular,
$x_{n_k} \mathrel {R} y_0 \mathrel {R} \dots \mathrel {R} y_m \mathrel {R} x_{n_k + 1 }$
. In particular,
![]() $Y_k \neq \emptyset $
.
$Y_k \neq \emptyset $
.
Towards a contradiction, suppose there are indices
![]() $k < j$
such that
$k < j$
such that
![]() $Y_k \cap Y_j \neq \emptyset $
. Pick
$Y_k \cap Y_j \neq \emptyset $
. Pick
![]() $y \in Y_k \cap Y_j$
. Then
$y \in Y_k \cap Y_j$
. Then
![]() $y \mathrel {R^+} x_{ n_k + 1 } \mathrel {R^+} x_{n_j} \mathrel {R^+} y$
, if
$y \mathrel {R^+} x_{ n_k + 1 } \mathrel {R^+} x_{n_j} \mathrel {R^+} y$
, if
![]() $x_{ n_k + 1 } \neq x_{n_j}$
, or
$x_{ n_k + 1 } \neq x_{n_j}$
, or
![]() $y \mathrel {R^+} x_{ n_k + 1 } = x_{n_j} \mathrel {R^+} y$
otherwise. Either way, this contradicts our assumption that R is acyclic.
$y \mathrel {R^+} x_{ n_k + 1 } = x_{n_j} \mathrel {R^+} y$
otherwise. Either way, this contradicts our assumption that R is acyclic.
Now we let
![]() $R_Y$
be the relation on
$R_Y$
be the relation on
![]() $\bigcup _{k \in \omega } Y_k$
$\bigcup _{k \in \omega } Y_k$
It readily follows from the definition that
![]() $R_Y \subseteq R^+$
.
$R_Y \subseteq R^+$
.
Claim 5.2.4.
![]() $R_Y$
is total on
$R_Y$
is total on
![]() $\bigcup _{k \in \omega } Y_k$
.
$\bigcup _{k \in \omega } Y_k$
.
Proof Pick
![]() $k \in \omega $
and
$k \in \omega $
and
![]() $y \in Y_k$
, towards proving that
$y \in Y_k$
, towards proving that
![]() $y \in \operatorname {\mathrm {dom}} ( R_Y )$
. Then there is a finite sequence
$y \in \operatorname {\mathrm {dom}} ( R_Y )$
. Then there is a finite sequence
![]() $\mathopen \langle y_0 , \dots , y_m \mathclose \rangle $
of elements of
$\mathopen \langle y_0 , \dots , y_m \mathclose \rangle $
of elements of
![]() $Y_k$
such that
$Y_k$
such that
![]() $x_{n_k} \mathrel {R} y_0 \mathrel {R} \dots \mathrel {R} y_m \mathrel {R} x_{n_k + 1}$
, and
$x_{n_k} \mathrel {R} y_0 \mathrel {R} \dots \mathrel {R} y_m \mathrel {R} x_{n_k + 1}$
, and
![]() $y = y_i$
for some
$y = y_i$
for some
![]() $0 \leq i \leq m$
. If
$0 \leq i \leq m$
. If
![]() $i < m$
, then
$i < m$
, then
![]() $y \mathrel {R} y_{i + 1}$
. If
$y \mathrel {R} y_{i + 1}$
. If
![]() $i = m$
then
$i = m$
then
![]() $y \mathrel {R_Y} y'$
for any
$y \mathrel {R_Y} y'$
for any
![]() $y' \in Y_{ k + 1}$
such that
$y' \in Y_{ k + 1}$
such that
![]() $x_{n_{k+1}} \mathrel {R} y'$
. In either case
$x_{n_{k+1}} \mathrel {R} y'$
. In either case
![]() $y \in \operatorname {\mathrm {dom}} ( R_Y )$
.
$y \in \operatorname {\mathrm {dom}} ( R_Y )$
.
By
![]() $\mathsf {DC} ( Y )$
, there is an
$\mathsf {DC} ( Y )$
, there is an
![]() $R_Y$
-chain
$R_Y$
-chain
![]() $( y_n )_{ n \in \omega }$
. By part (b) of Proposition 2.1 we can suppose that
$( y_n )_{ n \in \omega }$
. By part (b) of Proposition 2.1 we can suppose that
![]() $y_0 \in Y_0$
and that
$y_0 \in Y_0$
and that
![]() $x_{n_0} \mathrel {R} y_0$
. As the
$x_{n_0} \mathrel {R} y_0$
. As the
![]() $Y_k$
s are disjoint, for every n there is a unique k such that
$Y_k$
s are disjoint, for every n there is a unique k such that
![]() $y_n \in Y_k$
, and let
$y_n \in Y_k$
, and let
![]() $i ( n )$
be this k.
$i ( n )$
be this k.
Claim 5.2.5. The set
![]() $I_k = \mathopen \{{ n \in \omega }\boldsymbol \mid { i ( n ) = k } \mathclose \}$
is a finite interval of natural numbers.
$I_k = \mathopen \{{ n \in \omega }\boldsymbol \mid { i ( n ) = k } \mathclose \}$
is a finite interval of natural numbers.
Proof By definition of
![]() $R_Y$
it follows that either
$R_Y$
it follows that either
![]() $i ( n + 1 ) = i ( n )$
or else
$i ( n + 1 ) = i ( n )$
or else
![]() $i ( n + 1 ) = i ( n ) + 1$
, so it is enough to show that
$i ( n + 1 ) = i ( n ) + 1$
, so it is enough to show that
![]() $I_k$
is finite. Towards a contradiction, suppose
$I_k$
is finite. Towards a contradiction, suppose
![]() $I_{\bar {k}}$
is infinite, for some
$I_{\bar {k}}$
is infinite, for some
![]() $\bar {k} \in \omega $
. This means that there is
$\bar {k} \in \omega $
. This means that there is
![]() $\bar {n}$
such that
$\bar {n}$
such that
![]() $i ( n ) = i ( \bar {n} )$
for all
$i ( n ) = i ( \bar {n} )$
for all
![]() $n \geq \bar {n}$
, that is
$n \geq \bar {n}$
, that is
![]() $\mathopen \{{ y_n }\boldsymbol \mid { n \geq \bar {n} } \mathclose \} \subseteq Y_{\bar {k}}$
. But then
$\mathopen \{{ y_n }\boldsymbol \mid { n \geq \bar {n} } \mathclose \} \subseteq Y_{\bar {k}}$
. But then
![]() $R {\mathop {\upharpoonright }} \mathopen \{{ y_n }\boldsymbol \mid { n \geq \bar {n} } \mathclose \}$
would be a total on
$R {\mathop {\upharpoonright }} \mathopen \{{ y_n }\boldsymbol \mid { n \geq \bar {n} } \mathclose \}$
would be a total on
![]() $\mathopen \{{ y_n }\boldsymbol \mid { n \geq \bar {n} } \mathclose \}$
and contained in
$\mathopen \{{ y_n }\boldsymbol \mid { n \geq \bar {n} } \mathclose \}$
and contained in
![]() $R {\mathop {\upharpoonright }} Y$
, against (16).
$R {\mathop {\upharpoonright }} Y$
, against (16).
Let
![]() $m_k = \max ( I_k )$
so that
$m_k = \max ( I_k )$
so that
![]() $I_0 = [ 0; m_0 ]$
and
$I_0 = [ 0; m_0 ]$
and
![]() $I_{k + 1} = [ m_k + 1; m_{ k+1} ]$
. Then
$I_{k + 1} = [ m_k + 1; m_{ k+1} ]$
. Then
 $$ \begin{align*} \mathopen \langle x_0 , \dots , x_{ n_0 } \mathclose \rangle &{}^\smallfrown \mathopen \langle y_0 , \dots , y_{ m_0 } \mathclose \rangle {}^\smallfrown \mathopen \langle x_{ n_0 + 1 } , \dots , x_{ n_1 } \mathclose \rangle{}^\smallfrown \mathopen \langle y_{ m_0 + 1 } , \dots , y_{ m_1 } \mathclose \rangle {}^\smallfrown \dots \\ &\dots {}^\smallfrown \mathopen \langle x_{ n_k + 1 } , \dots , x_{ n_{ k + 1 } } \mathclose \rangle{}^\smallfrown \mathopen \langle y_{ m_k + 1 } , \dots , y_{ m_{ k + 1 } } \mathclose \rangle {}^\smallfrown \dots \end{align*} $$
$$ \begin{align*} \mathopen \langle x_0 , \dots , x_{ n_0 } \mathclose \rangle &{}^\smallfrown \mathopen \langle y_0 , \dots , y_{ m_0 } \mathclose \rangle {}^\smallfrown \mathopen \langle x_{ n_0 + 1 } , \dots , x_{ n_1 } \mathclose \rangle{}^\smallfrown \mathopen \langle y_{ m_0 + 1 } , \dots , y_{ m_1 } \mathclose \rangle {}^\smallfrown \dots \\ &\dots {}^\smallfrown \mathopen \langle x_{ n_k + 1 } , \dots , x_{ n_{ k + 1 } } \mathclose \rangle{}^\smallfrown \mathopen \langle y_{ m_k + 1 } , \dots , y_{ m_{ k + 1 } } \mathclose \rangle {}^\smallfrown \dots \end{align*} $$
is the required R-chain.
5.2 The Feferman–Levy model
Feferman and Levy showed that the following is consistent relative to
![]() $\mathsf {ZF}$
:
$\mathsf {ZF}$
:
(See [Reference Jech2, p. 142] for an exposition of the Feferman–Levy model.)
The next result shows that in the Feferman–Levy model, the statement of Theorem 4.1 fails, that is, there is no set
![]() $A \subseteq \mathbb {R}$
such that
$A \subseteq \mathbb {R}$
such that
![]() $\mathsf {DC} ( A )$
and
$\mathsf {DC} ( A )$
and
![]() $\neg {\mathsf {AC}}_\omega ( A )$
.
$\neg {\mathsf {AC}}_\omega ( A )$
.
Proposition 5.3.
![]() $\mathsf {FL}$
implies that if
$\mathsf {FL}$
implies that if
![]() $\mathsf {DC} ( A )$
holds with
$\mathsf {DC} ( A )$
holds with
![]() $A \subseteq \mathbb {R}$
, then A is countable.
$A \subseteq \mathbb {R}$
, then A is countable.
We need a preliminary result.
Lemma 5.4. Assume
![]() $\mathsf {FL}$
. Then there is a sequence of nonempty, countable, pairwise disjoint sets
$\mathsf {FL}$
. Then there is a sequence of nonempty, countable, pairwise disjoint sets
![]() $( X_n )_{ n \in \omega }$
such that
$( X_n )_{ n \in \omega }$
such that
![]() $\mathbb {R} = \bigcup _{n} X_n$
, and no infinite subsequence of
$\mathbb {R} = \bigcup _{n} X_n$
, and no infinite subsequence of
![]() $( X_n)_{ n \in \omega }$
has a choice function.
$( X_n)_{ n \in \omega }$
has a choice function.
Proof Fix a bijection
![]() $\pi \colon \mathbb {R} \to \mathbb {R}^\omega $
, and for each
$\pi \colon \mathbb {R} \to \mathbb {R}^\omega $
, and for each
![]() $m \in \omega $
let
$m \in \omega $
let
![]() $\pi _m \colon \mathbb {R} \to \mathbb {R}$
be defined as
$\pi _m \colon \mathbb {R} \to \mathbb {R}$
be defined as
![]() $\pi _m ( x ) = \pi ( x )_m$
. If
$\pi _m ( x ) = \pi ( x )_m$
. If
![]() $Y \subseteq \mathbb {R}$
and
$Y \subseteq \mathbb {R}$
and
![]() $f \colon \omega \to Y$
is surjective, then
$f \colon \omega \to Y$
is surjective, then
![]() $\tilde {Y}$
, the closure of Y under the
$\tilde {Y}$
, the closure of Y under the
![]() $\pi _m$
s, is also countable, as
$\pi _m$
s, is also countable, as
is surjective. By
![]() $\mathsf {FL}$
let
$\mathsf {FL}$
let
![]() $( Y_n )_{ n \in \omega }$
be a sequence of countable sets such that
$( Y_n )_{ n \in \omega }$
be a sequence of countable sets such that
![]() $\mathbb {R} = \bigcup _n Y_n$
, and without loss of generality we may assume that each
$\mathbb {R} = \bigcup _n Y_n$
, and without loss of generality we may assume that each
![]() $Y_n$
is closed under every
$Y_n$
is closed under every
![]() $\pi _m$
. Then let
$\pi _m$
. Then let
![]() $X_n = Y_n \setminus \bigcup _{m < n} Y_m$
for each
$X_n = Y_n \setminus \bigcup _{m < n} Y_m$
for each
![]() $n \in \omega $
. If necessary, we can pass to a subsequence to get them to be nonempty.
$n \in \omega $
. If necessary, we can pass to a subsequence to get them to be nonempty.
We claim that no infinite subsequence of
![]() $( X_n )_{ n \in \omega }$
has a choice function. Otherwise there would be an infinite sequence
$( X_n )_{ n \in \omega }$
has a choice function. Otherwise there would be an infinite sequence
![]() $( x_n )_{ n \in \omega } \in \mathbb {R}^\omega $
whose range intersects infinitely many
$( x_n )_{ n \in \omega } \in \mathbb {R}^\omega $
whose range intersects infinitely many
![]() $X_n$
s. Let
$X_n$
s. Let
![]() $x \in \mathbb {R}$
be such that
$x \in \mathbb {R}$
be such that
![]() $\pi ( x) = ( x_n )_{n \in \omega }$
. Then
$\pi ( x) = ( x_n )_{n \in \omega }$
. Then
![]() $x \in X_k \subseteq Y_k$
for some
$x \in X_k \subseteq Y_k$
for some
![]() $k \in \omega $
, and hence
$k \in \omega $
, and hence
as
![]() $Y_k$
is closed under the
$Y_k$
is closed under the
![]() $\pi _n$
s. But this contradicts the assumption that
$\pi _n$
s. But this contradicts the assumption that
![]() $\mathopen \{{ x_n }\boldsymbol \mid { n \in \omega } \mathclose \}$
intersects infinitely many
$\mathopen \{{ x_n }\boldsymbol \mid { n \in \omega } \mathclose \}$
intersects infinitely many
![]() $X_n$
s.
$X_n$
s.
Proof of Proposition 5.3
Fix
![]() $( X_n )_{ n \in \omega }$
as in Lemma 5.4. Let
$( X_n )_{ n \in \omega }$
as in Lemma 5.4. Let
![]() $A \subseteq \mathbb {R}$
such that
$A \subseteq \mathbb {R}$
such that
![]() $\mathsf {DC} ( A )$
holds, and let
$\mathsf {DC} ( A )$
holds, and let
![]() $I = \mathopen \{{ n \in \omega }\boldsymbol \mid { A \cap X_n \neq \emptyset } \mathclose \}$
. If I is infinite then, by part (c) of Proposition 2.1,
$I = \mathopen \{{ n \in \omega }\boldsymbol \mid { A \cap X_n \neq \emptyset } \mathclose \}$
. If I is infinite then, by part (c) of Proposition 2.1,
![]() $\mathsf {DC} ( A )$
would imply the existence of a choice function for the family
$\mathsf {DC} ( A )$
would imply the existence of a choice function for the family
![]() $ \mathopen \{{ A \cap X_n}\boldsymbol \mid { n \in I } \mathclose \}$
, which is, in particular, a choice function for
$ \mathopen \{{ A \cap X_n}\boldsymbol \mid { n \in I } \mathclose \}$
, which is, in particular, a choice function for
![]() $\mathopen \{{ X_n }\boldsymbol \mid { n \in I } \mathclose \}$
, against Lemma 5.4. So I must be finite, that is
$\mathopen \{{ X_n }\boldsymbol \mid { n \in I } \mathclose \}$
, against Lemma 5.4. So I must be finite, that is
![]() $A \subseteq X_0 \cup \dots \cup X_k$
for some k. But the finite union of countable sets is countable, so A is countable.
$A \subseteq X_0 \cup \dots \cup X_k$
for some k. But the finite union of countable sets is countable, so A is countable.
5.3 Definability of the counterexample
Theorem 4.1 shows that the statement (3) is consistent with
![]() $\mathsf {ZF}$
, that is to say, it is consistent that there is a set
$\mathsf {ZF}$
, that is to say, it is consistent that there is a set
![]() $A \subseteq \mathbb {R}$
such that
$A \subseteq \mathbb {R}$
such that
![]() $\mathsf {DC} ( A )$
and
$\mathsf {DC} ( A )$
and
![]() $\neg {\mathsf {AC}}_\omega ( A )$
. The set A constructed in the proof of Theorem 4.1 is a set of Cohen reals, so it is not ordinal definable. But what is the possible descriptive complexity of a set A as above?
$\neg {\mathsf {AC}}_\omega ( A )$
. The set A constructed in the proof of Theorem 4.1 is a set of Cohen reals, so it is not ordinal definable. But what is the possible descriptive complexity of a set A as above?
By part (c) of Proposition 2.5, the set A cannot contain a perfect set. Recall that a set has the perfect set property if it is either countable or else it contains a perfect subset. Assuming
![]() ${\mathsf {AC}}_\omega ( \mathbb {R} )$
, every Borel set has the perfect-set property. In a choice-less context the situation becomes murky. Assuming
${\mathsf {AC}}_\omega ( \mathbb {R} )$
, every Borel set has the perfect-set property. In a choice-less context the situation becomes murky. Assuming
![]() $\mathsf {FL}$
, every set of reals is
$\mathsf {FL}$
, every set of reals is
![]() $\mathbf {F}_{\sigma \sigma }$
(i.e., countable union of
$\mathbf {F}_{\sigma \sigma }$
(i.e., countable union of
![]() $\mathbf {F}_\sigma $
sets), and by taking complements it is also
$\mathbf {F}_\sigma $
sets), and by taking complements it is also
![]() $\mathbf {G}_{\delta \delta }$
(i.e., countable intersection of
$\mathbf {G}_{\delta \delta }$
(i.e., countable intersection of
![]() $\mathbf {G}_\delta $
sets), so every set is
$\mathbf {G}_\delta $
sets), so every set is
![]() $\boldsymbol {\Delta }^{0}_{4}$
, as
$\boldsymbol {\Delta }^{0}_{4}$
, as
![]() $\mathbf {F}_\sigma = \boldsymbol {\Sigma }^{0}_{2} \subset \boldsymbol {\Pi }^{0}_{3}$
, and hence
$\mathbf {F}_\sigma = \boldsymbol {\Sigma }^{0}_{2} \subset \boldsymbol {\Pi }^{0}_{3}$
, and hence
![]() $\mathbf {F}_{\sigma \sigma } \subseteq \boldsymbol {\Sigma }^{0}_{4}$
. Therefore
$\mathbf {F}_{\sigma \sigma } \subseteq \boldsymbol {\Sigma }^{0}_{4}$
. Therefore
![]() $\mathsf {FL}$
collapses the Borel hierarchy at level
$\mathsf {FL}$
collapses the Borel hierarchy at level
![]() $4$
. Moreover
$4$
. Moreover
![]() $\mathsf {FL}$
implies that there is an uncountable set in
$\mathsf {FL}$
implies that there is an uncountable set in
![]() $\boldsymbol {\Pi }^{0}_{3}$
without a perfect subset [Reference Miller8, Theorem 1.3].
$\boldsymbol {\Pi }^{0}_{3}$
without a perfect subset [Reference Miller8, Theorem 1.3].
On the other hand A. Miller has shown in
![]() $\mathsf {ZF}$
that
$\mathsf {ZF}$
that
![]() $\boldsymbol {\Sigma }^{0}_{3} \neq \boldsymbol {\Pi }^{0}_{3}$
[Reference Miller7, Theorem 2.1], and that every set in
$\boldsymbol {\Sigma }^{0}_{3} \neq \boldsymbol {\Pi }^{0}_{3}$
[Reference Miller7, Theorem 2.1], and that every set in
![]() $ \boldsymbol {\Sigma }^{0}_{3}$
has the perfect-set property [Reference Miller8, Theorem 1.2].
$ \boldsymbol {\Sigma }^{0}_{3}$
has the perfect-set property [Reference Miller8, Theorem 1.2].
Recall that a subset of
![]() $\mathbb {R}$
is
$\mathbb {R}$
is
![]() $\boldsymbol {\Pi }^{1}_{n}$
if it is the complement of a
$\boldsymbol {\Pi }^{1}_{n}$
if it is the complement of a
![]() $\boldsymbol {\Sigma }^{1}_{n}$
, and it is
$\boldsymbol {\Sigma }^{1}_{n}$
, and it is
![]() $\boldsymbol {\Sigma }^{1}_{n}$
if it is the projection of a
$\boldsymbol {\Sigma }^{1}_{n}$
if it is the projection of a
![]() $\boldsymbol {\Pi }^{1}_{n - 1}$
set
$\boldsymbol {\Pi }^{1}_{n - 1}$
set
![]() $C \subseteq \mathbb {R} \times \mathbb {R}$
, where
$C \subseteq \mathbb {R} \times \mathbb {R}$
, where
![]() $\boldsymbol {\Pi }^{1}_{0}$
is the collection of closed sets. The lightface hierarchy
$\boldsymbol {\Pi }^{1}_{0}$
is the collection of closed sets. The lightface hierarchy
![]() $\varSigma ^1_n , \varPi ^1_n$
is obtained by replacing
$\varSigma ^1_n , \varPi ^1_n$
is obtained by replacing
![]() $\boldsymbol {\Pi }^{1}_{0}$
with
$\boldsymbol {\Pi }^{1}_{0}$
with
![]() $\varPi ^1_0$
, the collection of recursively-closed sets (see [Reference Kanamori4, Chapter 3, Section 12]). Working in
$\varPi ^1_0$
, the collection of recursively-closed sets (see [Reference Kanamori4, Chapter 3, Section 12]). Working in
![]() $\mathsf {ZF}$
, every
$\mathsf {ZF}$
, every
![]() $\boldsymbol {\Sigma }^{1}_{1}$
set has the perfect set property, and by a theorem of Mansfield and Solovay (see [Reference Kanamori4, Chapter 3 and Corollary 14.9]) every
$\boldsymbol {\Sigma }^{1}_{1}$
set has the perfect set property, and by a theorem of Mansfield and Solovay (see [Reference Kanamori4, Chapter 3 and Corollary 14.9]) every
![]() $ \boldsymbol {\Sigma }^{1}_{2}$
set is either well-orderable, being included in
$ \boldsymbol {\Sigma }^{1}_{2}$
set is either well-orderable, being included in
![]() $\mathord {\mathrm {L}} [ a ]$
for some real a, or else it contains a perfect set.
$\mathord {\mathrm {L}} [ a ]$
for some real a, or else it contains a perfect set.
By part (c) of Lemma 2.5 we obtain the following:
Corollary 5.5. If
![]() $A \subseteq \mathbb {R}$
is
$A \subseteq \mathbb {R}$
is
![]() $\boldsymbol {\Sigma }^{0}_{3}$
or
$\boldsymbol {\Sigma }^{0}_{3}$
or
![]() $\boldsymbol {\Sigma }^{1}_{2}$
and
$\boldsymbol {\Sigma }^{1}_{2}$
and
![]() $\mathsf {DC} ( A )$
holds, then
$\mathsf {DC} ( A )$
holds, then
![]() ${\mathsf {AC}}_\omega ( A )$
.
${\mathsf {AC}}_\omega ( A )$
.
We conclude with a question.
Question 5.6. Is it consistent with
![]() $\mathsf {ZF}$
that there is a
$\mathsf {ZF}$
that there is a
![]() $\varPi ^{1}_{2}$
set
$\varPi ^{1}_{2}$
set
![]() $A \subseteq \mathbb {R}$
such that
$A \subseteq \mathbb {R}$
such that
![]() $\mathsf {DC} ( A )$
and
$\mathsf {DC} ( A )$
and
![]() $\neg {\mathsf {AC}}_\omega ( A )$
?
$\neg {\mathsf {AC}}_\omega ( A )$
?
Acknowledgement
The authors are grateful to the anonymous referee for the useful comments and suggestions.
Funding
This research was supported by the project PRIN 2017 “Mathematical Logic: models, sets, computability”, prot. 2017NWTM8R. The second author would also like to acknowledge INdAM for the financial support.