Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-09T03:56:14.444Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalizing special Aronszajn trees

Published online by Cambridge University Press:  12 March 2014

James H. Schmerl
James H. Schmerl*
Affiliation:
University of Connecticut, Storrs, Connecticut 06268
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we define by means of a partition property a decreasing sequence N = ‹Nα: α is an ordinal› of classes of ordinals. This property is a generalization of the nonexistence of special Aronszajn trees: the successor cardinal κ+ is in N0 iff there does not exist a special Aronszajn κ+-tree.

The interest in the classes Nα stems from their applicability in model theory, in particular to that aspect of model theory dealing with ordered and two-cardinal models. A model 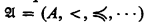is κ-like iff < is a linear ordering of A of cardinality κ but such that every proper initial segment has cardinality < κ. 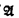is α-ordered iff ≼ is a reflexive, linear ordering of some subset of A with order type α. The sequence N can be characterized by a first-order sentence σ in the following manner: The sentence σ has a κ-like α-ordered model iff κ ∉ Nα. This characterization will allow us to translate various independence statements regarding the sequence N to statements about the independence of transfer properties. We say that the transfer property κ → λ holds iff every first-order sentence which has a κ-like model also has a λ-like model. κ ⇸ λ is the negation of κ → λ.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 39 , Issue 4 , December 1974 , pp. 732 - 740
Copyright
Copyright © Association for Symbolic Logic 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Barwise, Jon, Infinitary logic and admissible sets, this Journal, vol. 34 (1969), pp. 226–252.Google Scholar
[2] Boos, William, Boolean extensions which efface the Mahlo property (mimeographed).Google Scholar
[3] Chang, C. C., A note on the two cardinal problem, Proceedings of the American Mathematical Society, vol. 16 (1965), pp. 1148–1155.Google Scholar
[4] Erdös, P., Hajnal, A. and Rado, R., Partition relations for cardinal numbers, Acta Mathematica, vol. 16 (1965), pp. 93–196.Google Scholar
[5] Erdös, P. and Rado, R., A partition calculus in set theory, Bulletin of the American Mathematical Society, vol. 62 (1956), pp. 427–489.Google Scholar
[6] Jensen, R. B., The fine structure of the constructible hierarchy, Annals of Mathematical Logic, vol. 4 (1972), pp. 229–308.Google Scholar
[7] Lévy, A., A hierarchy of formulas in set theory, Memoirs of the American Mathematical Society, No. 57 (1965).Google Scholar
[8] Mitchell, William, Aronszajn trees and the independence of the transfer property, Annals of Mathematical Logic, vol. 5 (1972), pp. 21–46.CrossRefGoogle Scholar
[9] Morley, M. and Vaught, R., Homogeneous universal models, Mathematica Scandinavica, vol. 11 (1962), pp. 37–57.CrossRefGoogle Scholar
[10] Schmerl, J. H., On κ-like models for inaccessible κ, Doctoral Dissertation, University of California, Berkeley, 1971.Google Scholar
[11] Schmerl, J. H., An elementary sentence which has ordered models, this Journal, vol. 37 (1972), pp. 521–530.Google Scholar
[12] Schmerl, J. H., A partition property characterizing cardinals hyperinaccessible of finite type, Transactions of the American Mathematical Society, vol. 188 (1974), pp. 281–291.Google Scholar
[13] Schmerl, J. H. and Shelah, S., On power-like models for hyperinaccessible cardinals, this Journal, vol. 37 (1972), pp. 531–537.Google Scholar