Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T10:39:26.075Z Has data issue: false hasContentIssue false
  • English
  • Français

A MODEL-THEORETIC CHARACTERIZATION OF MONADIC SECOND ORDER LOGIC ON INFINITE WORDS

Published online by Cambridge University Press:  21 March 2017

SILVIO GHILARDI  and
SAMUEL J. VAN GOOL
SILVIO GHILARDI
Affiliation:
DIPARTIMENTO DI MATEMATICA UNIVERSITÀ DEGLI STUDI DI MILANO MILAN, ITALYE-mail: silvio.ghilardi@unimi.it
SAMUEL J. VAN GOOL
Affiliation:
DEPARTMENT OF MATHEMATICS CITY COLLEGE OF NEW YORK NEW YORK, USAE-mail: samvangool@me.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Monadic second order logic and linear temporal logic are two logical formalisms that can be used to describe classes of infinite words, i.e., first-order models based on the natural numbers with order, successor, and finitely many unary predicate symbols.

Monadic second order logic over infinite words (S1S) can alternatively be described as a first-order logic interpreted in 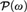${\cal P}\left( \omega \right)$, the power set Boolean algebra of the natural numbers, equipped with modal operators for ‘initial’, ‘next’, and ‘future’ states. We prove that the first-order theory of this structure is the model companion of a class of algebras corresponding to a version of linear temporal logic (LTL) without until.

The proof makes crucial use of two classical, nontrivial results from the literature, namely the completeness of LTL with respect to the natural numbers, and the correspondence between S1S-formulas and Büchi automata.

Keywords

Primary 03B70Secondary 03B4403C6068Q45linear temporal logicmonadic second order logicBüchiautomatamodel completeness
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 1 , March 2017 , pp. 62 - 76
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Blackburn, P., de Rijke, M., and Venema, Y., Modal Logic, Cambridge Tracts in Theoretical Computer Science, vol. 53, Cambridge University Press, Cambridge, 2001.Google Scholar
Büchi, J. R., On a decision method in restricted second-order arithmetic , Proceedings 1960 International Congress for Logic, Methodology and Philosophy of Science (Nagel, E., Suppes, P., and Tarski, A., editors), Stanford University Press, Stanford, 1962, pp. 1–11.Google Scholar
Esakia, L., Topological Kripke models . Soviet Mathematics Doklady, vol. 15 (1974), pp. 147–151.Google Scholar
Fine, K., Some connections between elementary and modal logic , Proceedings of the Third Scandinavian Logic Symposium (Kanger, S., editor), North-Holland, Amsterdam, 1975, pp. 15–31.CrossRefGoogle Scholar
Gehrke, M., Canonical extensions, Esakia spaces, and universal models , Leo Esakia on Duality in Modal and Intuitionistic Logics (Bezhanishvili, G., editor), Springer, Dordrecht, 2014, pp. 9–42.Google Scholar
Gehrke, M., Grigorieff, S., and Pin, J.-É., Duality and equational theory of regular languages , 35th International Colloquium on Automata, Languages and Programming (ICALP 2008) (Aceto, L., Damgård, I., Ann Goldberg, L., Halldórsson, M. M., Ingólfsdóttir, A., and Walukiewicz, I., editors), Lecture Notes in Computer Science, vol. 5126, Springer, Berlin, Heidelberg, 2008, pp. 246–257.Google Scholar
Gehrke, M., Krebs, A., and Pin, J.-É., From ultrafilters on words to the expressive power of a fragment of logic , Descriptional Complexity of Formal Systems (DCFS 2014) (Jürgensen, H., Karhumäki, J., and Okhotin, A., editors), Lecture Notes in Computer Science, vol. 8614, Springer, Switzerland, 2014, pp. 138–149.Google Scholar
Gheerbrant, A. and Ten Cate, B., Complete axiomatizations of fragments of monadic second-order logic on finite trees . Logical Methods in Computer Science, vol. 8 (2012), no. 4, p. 12.Google Scholar
Goldblatt, R., Varieties of complex algebras . Annals of Pure and Applied Logic, vol. 44 (1989), pp. 173–242.Google Scholar
Goldblatt, R., Logics of Time and Computation, second ed., CSLI Lecture Notes, vol. 7, Stanford University, Stanford, 1992.Google Scholar
Grädel, E., Thomas, W., and Wilke, T. (eds.), Automata Logics, and Infinite Games: A Guide to Current Research, Lecture Notes in Computer Science, vol. 2500, Springer, Berlin, Heidelberg, 2002.Google Scholar
Pnueli, A., The temporal logic of programs , Proceedings of the 18th Annual Symposium on Foundations of Computer Science (FOCS) (Greibach, S., Kosaraju, S., Lynch, N., Rivest, R., Rounds, W., Winograd, S., and Young, P., editors), IEEE Computer Society, Long Beach, CA, 1977, pp. 46–57.Google Scholar
Riba, C., A model theoretic proof of completeness of an axiomatization of monadic second-order logic on infinite words , Theoretical Computer Science 2012, Lecture Notes in Computer Science, vol. 7604, Springer, Berlin, Heidelberg, 2012, pp. 310–324.CrossRefGoogle Scholar
Robinson, A., Introduction to Model Theory and to the Metamathematics of Algebra, Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam, 1963.Google Scholar
Thomas, W., Languages, automata, and logic, Technical Report 9607, Institut für Informatik und Praktische Mathematik, Christian-Albrechts-Universität, Kiel, 1997.CrossRefGoogle Scholar
Wheeler, W. H., Model-companions and definability in existentially complete structures . Israel Journal of Mathematics, vol. 25 (1976), pp. 305–330.CrossRefGoogle Scholar