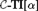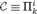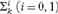Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sato, Kentaro
2020.
Elementary inductive dichotomy: Separation of open and clopen determinacies with infinite alternatives.
Annals of Pure and Applied Logic,
Vol. 171,
Issue. 3,
p.
102754.
Arai, Toshiyasu
2020.
Ordinal Analysis with an Introduction to Proof Theory.
p.
175.
Sato, Kentaro
2020.
Ordinal analyses for monotone and cofinal transfinite inductions.
Archive for Mathematical Logic,
Vol. 59,
Issue. 3-4,
p.
277.
Sato, Kentaro
2022.
Bounded inductive dichotomy: separation of open and clopen determinacies with finite alternatives in constructive contexts.
Archive for Mathematical Logic,
Vol. 61,
Issue. 3-4,
p.
399.
NEMOTO, TAKAKO
and
KENTARO, SATO
2022.
A MARRIAGE OF BROUWER’S INTUITIONISM AND HILBERT’S FINITISM I: ARITHMETIC.
The Journal of Symbolic Logic,
Vol. 87,
Issue. 2,
p.
437.
KENTARO, SATO
and
WALKER, JAN
2023.
FINITIST AXIOMATIC TRUTH.
The Journal of Symbolic Logic,
Vol. 88,
Issue. 1,
p.
22.
Sato, Kentaro
2023.
A new model construction by making a detour via intuitionistic theories III: Ultrafinitistic proofs of conservations of Σ11 collection.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 3,
p.
103207.