Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Morillon, Marianne
2012.
Helly Spaces and Radon Measures on Complete Lines.
Order,
Vol. 29,
Issue. 3,
p.
419.
Keremedis, Kyriakos
2012.
Compact and Loeb Hausdorff spaces in \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$\mathsf {ZF}$\end{document} and the axiom of choice for families of finite sets.
Mathematical Logic Quarterly,
Vol. 58,
Issue. 3,
p.
130.
Keremedis, Kyriakos
and
Wajch, Eliza
2020.
On Loeb and sequential spaces in ZF.
Topology and its Applications,
Vol. 280,
Issue. ,
p.
107279.

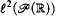 is not provable in
is not provable in 