Article contents
On deciding the truth of certain statements involving the notion of consistency
Published online by Cambridge University Press: 12 March 2014
Extract
Friedman has posed (see [F, p. 117]) the following problem: “35. Define the set E of expressions by (i) Con is an expression; (ii) if A, B are expressions so are (~ A), (A&B), and Con(A). Each expression ϕ in E determines a sentence ϕ in PA [classical first-order arithmetic] by taking Con* to be “PA is consistent,” ( ~ A) * to be ~ (A*), (A&B)* to be A*&B*, and Con(A)* to be “PA + ‘A*’ is consistent.” The set of expressions ϕ ∈ E such that ϕ* is true is recursive.
The formalized second incompleteness theorem reads
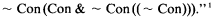
In order to simplify notation, we will reformulate Friedman's problem slightly. Let Con be the usual sentence of PA expressing the consistency of PA, ~ A the negation of A, (A&B) the conjunction of A and B, etc., and Bew(A) the result of substituting the numeral for the Gödel number of A for the free variable in the usual provability predicate for PA. Let Con(A) = ~ Bew(~ A). (Con(A) is equivalent in PA to the usual sentence expressing the consistency of PA + A.) And let the class of F-sentences be the smallest class which contains Con and which also contains ~ A, (A&B) and Con(A) whenever it contains A and B. Since ⊦PA Bew(A) ↔ Bew(B) if ⊦PAA ↔ B, Friedman's problem is then the question whether the class of true F-sentences is recursive.
The answer is that it is recursive. To see why, we need a definition and a theorem.
Definition. An atom is a sentence Conn for some n ≥ 1, where Cont = Con and Conn + 1 = Con(Conn).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1976
References
REFERENCES
- 9
- Cited by

