Logical falsehoods are usually barred in confirmation theory from serving as evidence statements. I wish to study here some three major ways in which this restriction can be lifted.

1. Consider the following axioms for the two-argument confirmation function C:

A1. 0 ≤ C(h, e) ≤ 1;

A2. If ⊦h ≡ h′ and ⊦e ≡ e′, then C(h, e) = C(h′, e′);

A3. If ⊦e ⊃ h, then C(h, e) = 1;

A4. If ⊦e ⊃ ˜(h.h′), then C(h⋁h′, e) = C(h, e)+C(h′, e);

A5. C(h.h′, e) = C(h,e)×C(h′, h.e);

where h, h′, e, and e′ are any four statements from a consistent language L and where ‘⊦’ is short for ‘is logically true in L.’ A1—A5 are consistent, as shown by the following construction:

C1. Let all four of h, h′, e, and e′ be some logical truth lt of L, and let C(h, e) equal 1 for any two h and e;

under which they become true. But they yield as consequences:

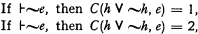
and hence

No statement e of L is logically false.

Since all the languages for which confirmation theories have been proposed contain logical falsehoods, (1) is undesirable. Restrictions must accordingly be placed upon some of A1—A5.