Hostname: page-component-7479d7b7d-c9gpj Total loading time: 0 Render date: 2024-07-10T13:27:47.687Z Has data issue: false hasContentIssue false
  • English
  • Français

Rings which admit elimination of quantifiers

Published online by Cambridge University Press:  12 March 2014

Bruce I. Rose
Bruce I. Rose*
Affiliation:
University of Notre Dame, Notre Dame, Indiana 46556
Get access Rights & Permissions [Opens in a new window]

Abstract

We say that a ring admits elimination of quantifiers, if in the language of rings, {0, 1, +, ·}, the complete theory of R admits elimination of quantifiers.

Theorem 1. Let D be a division ring. Then D admits elimination of quantifiers if and only if D is an algebraically closed or finite field.

A ring is prime if it satisfies the sentence: ∀x∀y∃z (x =0 ∨ y = 0∨ xzy ≠ 0).

Theorem 2. If R is a prime ring with an infinite center and R admits elimination of quantifiers, then R is an algebraically closed field.

Let 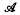be the class of finite fields. Let 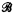be the class of 2 × 2 matrix rings over a field with a prime number of elements. Let 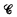be the class of rings of the form GF(pn)⊕GF(pk) such that either n = k or g.c.d. (n, k) = 1. Let 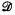be the set of ordered pairs (f, Q) where Q is a finite set of primes and 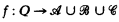such that the characteristic of the ring f(q) is q. Finally, let 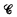be the class of rings of the form ⊕q ∈ Qf(q), for some (f, Q) in .

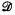Theorem 3. Let R be a finite ring without nonzero trivial ideals. Then R admits elimination of quantifiers if and only if R belongs to.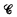

Theorem 4. Let R be a ring with the descending chain condition of left ideals and without nonzero trivial ideals. Then R admits elimination of quantifiers if and only if R is an algebraically closed field or R belongs to.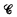

In contrast to Theorems 2 and 4, we have

Theorem 5. If R is an atomless p-ring, then R is finite, commutative, has no nonzero trivial ideals and admits elimination of quantifiers, but is not prime and does not have the descending chain condition.

We also generalize Theorems 1, 2 and 4 to alternative rings.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 1 , March 1978 , pp. 92 - 112
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baldwin, J. T. and Lachlan, A. H., On strongly minimal sets, this Journal, vol. 36 (1971), pp. 79–96.Google Scholar
[2]Baldwin, J. T. and Rose, B. I., ℵ0-categoricity and stability of rings, Journal of Algebra, vol. 45 (1977), pp. 1–16.CrossRefGoogle Scholar
[3]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1972.Google Scholar
[4]Cherlin, G. L. and Reineke, J., Categoricity and stability of commutative rings, Annals of Mathematical Logic, vol. 9 (1976), pp. 367–400.CrossRefGoogle Scholar
[5]Felgner, U., Ringe, deren Theorien ℵ1-categorich sind, Fundamenta Mathematicae, vol. 72 (1975), pp. 331–346.CrossRefGoogle Scholar
[6]Foster, A. L., p-rings and their Boolean-vector representation, Acta Mathematica, vol. 84 (1951), pp. 231–261.CrossRefGoogle Scholar
[7]Halmos, P. R., Lectures on Boolean algebras, Van Nostrand, Princeton, 1963.Google Scholar
[8]Herstein, I. N., Noncommutative rings, Mathematical Association of America Carus Monograph Series, vol. 15, The American Mathematical Society, Providence, R.I., 1968.Google Scholar
[9]Jacobson, N., Structure of rings, 2nd edition, American Mathematical Society Colloquium Publications, vol. 37, The American Mathematical Society, Providence, R.I., 1970.Google Scholar
[10]Kaplansky, I., Fields and rings, University of Chicago Press, Chicago, Illinois, 1969.Google Scholar
[11]Macintyre, A., On ω1-categorical theories of fields, Fundamenta Mathematicae, vol. 71 (1971), pp. 1–25.CrossRefGoogle Scholar
[12]Rose, B. I., Model theory of alternative rings, Ph.D. Thesis, University of Chicago, 1976.Google Scholar
[13]Sabbagh, G., Embedding problems for modules and rings with application to model-companions, Journal of Algebra, vol. 18 (1971), pp. 390–403.CrossRefGoogle Scholar
[14]Sacks, G. E., Saturated model theory, Benjamin, Reading, Massachusetts, 1972.Google Scholar
[15]Schafer, R. D., An introduction to nonassociative algebras, Academic Press, New York, 1966.Google Scholar
[16]Slater, M., Strongly prime alternative rings (to appear).Google Scholar
[17]Tarski, A., Contributions to the theory of models, Proceedings of the Royal Academy of Sciences, Amsterdam, series A, vol. 57 (1954), pp. 572–581, pp. 582–588 and vol. 58 (1955), pp. 56–64.Google Scholar