In this paper we shall use a logic with truth values ranging over all the real numbers x such that 0 ≦ x ≦ 1.1 will be “complete truth” and 0 will be “complete falsity.” The primitive sentential connectives are ‘⊃’ and ‘∼’; other connectives are ‘∨’ and ‘·’. Assume that ‘p’ and ‘q’ are sentential variables, whose truth values are respectively x and y. Then

1.1. ‘p ⊃ q’ has the value min(1 − x + y, 1),

1.2. ‘∼p’ has the value 1 − x,

1.3. ‘p∨q’ has the value max(x, y), and

1.4. ‘p·q’ has the value min (x, y).

‘∨’ and ‘·’ can be defined as follows:

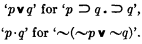
It is the purpose of this paper to prove a theorem which will be stated in the next section. The following symbolism and convention will be used throughout the paper:

S is a logical formula.

ν (S) is the value of S.

‘p’, ‘pi1, ’p2, …, ‘q’, are sentential variables.

ν(p) = x and ν(x1) = x1, etc.

ν(S) = σ and ν(S1) = σ1, etc.

If S contains the sentential variables ‘p1’, ‘p2’, …, then we write for S, S(p1, P2, …). Also ν{S(p1, p2, …)) = σ(x1, x2, …).

A logical formula is defined in the usual manner. 1. A sentential variable is a logical formula; 2. if S is a logical formula then ·S is a logical formula; and 3. if S and S′ are logical formulae then (S ⊃ S′) is a logical formula.

It is well known that certain sentences corresponding to similar algebras are invariant under direct union; that is, are true of the direct union when true of each factor algebra. An axiomatizable class of similar algebras, such as the class of groups, is closed under direct union when each of its axioms is invariant. In this paper we shall determine a wide class of invariant sentences. We shall also be concerned with determining sentences which are true of a direct union provided they are true of some factor algebra. In the case where all the factor algebras are the same, a further result is obtained. In §2 it will be shown that these criteria are the only ones of their kind. Lemma 7 below may be of some independent interest.

We adopt the terminology and notation of McKinsey with the exception that the sign · will be used for conjunction. Expressions of the form ∼∊, where ∊ is an equation, will be called inequalities. In accordance with the analogy between conjunction and disjunction with product and sum respectively, we shall call α1, …, αn the terms of the disjunction

and the factors of the conjunction

Every closed sentence is equivalent to a sentence in prenez normal form,

where x1, …, xm distinct individual variables, Q1, …, Qm are quantifiers, and the matrix S is an open sentence in which each of the variables x1, …, xm actually occurs. The sentence S may be written in either disjunctive normal form:

where αi,j is either an equation or an inequality, or in conjunctive normal form:

.

In part I of the present paper axiom schemes and rules of inference were defined for m-valued functional calculi of first order with s(m > s > 1) designated truth-values. A proof of plausibility was given, and it was shown that it is not difficult to extend to m-valued functional calculi of first order certain concepts that are closely analogous to the ordinary 2-valued notions of “consistency with respect to an operator” and “absolute consistency.” The purpose of the present paper is to show that the concept of “deductive completeness” may be extended to m-valued functional calculi of first order. For this purpose we define “analytic formula” for the m-valued case and show that if a formula is analytic, then it is provable in our formalization of m-valued functional calculi of first order.

In proving deductive completeness for the m-valued case, it is possible to use a method which is analogous to that used by Gödel in establishing the completeness of 2-valued functional calculi of first order. However, in the present paper we will indicate only very briefly how the Gödel procedure may be extended to the m-valued case. Our chief concern will be the problem of extending to our formalization of m-valued functional calculi the more elegant proof of deductive completeness for the 2-valued case which has recently been developed by Leon Henkin.

The purpose of this paper is to construct a non-finitary system of logic S, based on the theory of types, in which classical quantification theory holds without restriction and the axiom of reducibility holds with such slight restriction as is perhaps unlikely to interfere with the construction of classical mathematics. The system will be shown to be consistent.

For purposes of orientation, a rough description of the ontology of the system will first be given. The ‘individuals’ are expressions built up in the following way: ‘0’ is an individual, and if ϕ and ψ are individuals, so is ˹*ϕψ˺. The usual apparatus of truth functional connectives and quantifiers is employed, and one primitive four place predicate ‘S’. ˹Sϕψχω˺ says that ϕ is the result of writing ψ for all occurrences of χ in ω, where ϕ, ψ, χ and ω may be formulae, individuals, or members of a wider category called ‘expressions’ which includes individuals, formulae, and other things as well. (At first sight this looks like a confusion of use and mention, but the formation rules and rules of inference are so phrased that no ambiguity arises.)

The individuals are divided into types concentrically, so that type 0 has them all as members and type n includes type m for m > n. There is no highest type, but we shall find it convenient from the point of view of exposition to construct an infinity of ‘auxiliary’ systems Q(k), restricted to types ≦ k, before presenting the system S.

A general system of axioms has been given by Henkin for a fragment of the propositional calculus having as primitive symbols, in addition to the usual parentheses, variables, and implication sign ⊃, an arbitrarily given truth function symbol ϕ. This system of axioms, which we shall denote by S(⊃, ϕ), contains the following three axiom schemata

plus the 2m further axiom schemata involving the symbol ϕ

where ϕ is an m-placed function symbol. We refer to Henkin's paper, p. 43, for the detailed description of the axiom schemata (4).

The remark was made in the above mentioned paper that each of the 2m axiom schemata of (4) is trivially independent of the rest of the axioms of S(⊃, ϕ), and it was conjectured that the axiom schemata (1), (2) and (3) are also independent. In this note, we prove the general independence of the axiom schemata (1) and (2). As for (3), we show on the one hand its independence in the systems S(⊃) and S(⊃, f), and, on the other hand, its dependence in the system S(⊃, ∼). The net result is, therefore, that in any of these systems of axioms S(⊃, ϕ) all the axiom schemata are independent, except possibly the axiom schema (3).