Hostname: page-component-7857688df4-8r446 Total loading time: 0 Render date: 2025-11-19T22:25:59.873Z Has data issue: false hasContentIssue false
  • English
  • Français

A MINIMAL CONGRUENCE LATTICE REPRESENTATION FOR 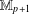$\mathbb{M}_{p+1}$

Part of: Lattices Algebraic logic Algebraic structures

Published online by Cambridge University Press:  24 March 2020

ROGER BUNN ,
DAVID GROW ,
MATT INSALL Open the ORCID record for MATT INSALL [Opens in a new window]  and
PHILIP THIEM
ROGER BUNN
Affiliation:
Missouri State University, 901 South National Avenue, Springfield, MO65897, USA email RogerBunn@missouristate.edu
DAVID GROW
Affiliation:
Missouri University of Science and Technology, 202 Rolla Building, Rolla, MO65409-0020, USA email grow@mst.edu
MATT INSALL*
Affiliation:
Missouri University of Science and Technology, Mathematics & Statistics, 400 W 12th Street, Room 315 Rolla Building, Rolla, MO65409, USA email insall@mst.edu
PHILIP THIEM
Affiliation:
Missouri University of Science and Technology, 202 Rolla Building, Rolla, MO65409-0020, USA email ptt@mst.edu
*
✉insall@mst.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 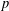$p$ be an odd prime. The unary algebra consisting of the dihedral group of order 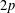$2p$, acting on itself by left translation, is a minimal congruence lattice representation of 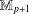$\mathbb{M}_{p+1}$.

Keywords

06B15universal algebracongruence lattice representation

MSC classification

Primary: 03G10: Lattices and related structures 06B15: Representation theory 08A60: Unary algebras 08A62: Finitary algebras

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 3 , June 2020 , pp. 332 - 340
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

References

Alm, J. and Snow, J., ‘Lattices of equivalence relations closed under the operations of relation algebras’, Algebra Univers. 71 (2014), 187–190.10.1007/s00012-014-0270-7CrossRefGoogle Scholar
Aschbacher, M., ‘Overgroups of primitive groups, II’, J. Algebra 322 (2009), 1586–1626.10.1016/j.jalgebra.2009.04.044CrossRefGoogle Scholar
Baddely, R., ‘A new approach to the finite lattice representation problem’, Period. Math. Hungar. 36 (1998), 17–59.10.1023/A:1004607902533CrossRefGoogle Scholar
DeMeo, W., ‘Expansions of finite algebras and their congruence lattices’, Algebra Universalis 69 (2013), 257–278.10.1007/s00012-013-0226-3CrossRefGoogle Scholar
Dixon, J. D. and Mortimer, B., Permutation Groups (Springer, New York, 1996).10.1007/978-1-4612-0731-3CrossRefGoogle Scholar
Grätzer, G., Universal Algebra, 2nd edn (Springer, New York, 1979).Google Scholar
Grätzer, G., General Lattice Theory, 2nd edn (Birkhäuser, Basel, 1998).Google Scholar
Hall, M., The Theory of Groups (Macmillan, New York, 1959).Google Scholar
Harary, F., Graph Theory (Addison-Wesley, Reading, MA, 1969).10.21236/AD0705364CrossRefGoogle Scholar
Lucchini, A., ‘Representation of certain lattices as intervals in subgroup lattices’, J. Algebra 164 (1994), 85–90.10.1006/jabr.1994.1054CrossRefGoogle Scholar
McKenzie, R. N., McNulty, G. F. and Taylor, W. F., Algebras, Lattices, Varieties, Wadsworth & Brooks/Cole Mathematics Series, vol. I (Wadsworth & Brooks/Cole, Monterey, CA, 1987).Google Scholar
McNulty, G. F., ‘A juggler’s dozen of easy problems’, Algebra Universalis 74 (2015), 17–34.CrossRefGoogle Scholar
Pálfy, P. P., ‘Intervals in subgroup lattices of finite groups’, in: Groups ’93 Galway/St. Andrews, Vol. 2, London Mathematical Society Lecture Note Series, 212 (Cambridge University Press, Cambridge, 1995), 482–494.10.1017/CBO9780511629297.014CrossRefGoogle Scholar
Pálfy, P. P., ‘Groups and lattices’, in: Groups ’01 St. Andrews/Oxford, Vol. 2, London Mathematical Society Lecture Note Series, 305 (Cambridge University Press, Cambridge, 2003), 428–454.Google Scholar
Pálfy, P. P. and Pudlák, P., ‘Congruence lattices of finite algebras and intervals in subgroup lattices of finite groups’, Algebra Universalis 11 (1980), 22–27.10.1007/BF02483080CrossRefGoogle Scholar
Snow, J., ‘A constructive approach to the finite congruence lattice representation problem’, Algebra Universalis 43 (2000), 279–293.10.1007/s000120050159CrossRefGoogle Scholar
Stone, M. G. and Weedmark, R. H., ‘On representing 𝕄n’s by congruence lattices of finite algebras’, Discrete Math. 44 (1983), 299–308.10.1016/0012-365X(83)90195-4CrossRefGoogle Scholar