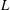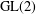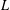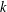Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Liu, Sheng-Chi
Masri, Riad
and
Young, Matthew P.
2015.
Rankin–Selberg L-functions and the reduction of CM elliptic curves.
Research in the Mathematical Sciences,
Vol. 2,
Issue. 1,
Balkanova, Olga
and
Frolenkov, Dmitry
2018.
Non-vanishing of automorphic L-functions of prime power level.
Monatshefte für Mathematik,
Vol. 185,
Issue. 1,
p.
17.
Knightly, Andrew
and
Reno, Caroline
2019.
Weighted Distribution of Low-lying Zeros of GL(2) -functions.
Canadian Journal of Mathematics,
Vol. 71,
Issue. 1,
p.
153.