Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kopperman, R.D.
1993.
Which topologies are quasimetrizable?.
Topology and its Applications,
Vol. 52,
Issue. 2,
p.
99.
Ivanov, A. A.
1996.
Bibliography on bitopological spaces. 2.
Journal of Mathematical Sciences,
Vol. 81,
Issue. 2,
p.
2497.
Künzi, Hans-Peter A.
2001.
Handbook of the History of General Topology.
Vol. 3,
Issue. ,
p.
853.
Andrikopoulos, Athanasios
2007.
The Quasimetrization Problem in the (Bi)topological Spaces.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2007,
Issue. ,
p.
1.
Marín, Josefa
2009.
Weak bases and quasi-pseudo-metrization of bispaces.
Topology and its Applications,
Vol. 156,
Issue. 18,
p.
3070.
Minguzzi, E.
2012.
Quasi-pseudo-metrization of topological preordered spaces.
Topology and its Applications,
Vol. 159,
Issue. 12,
p.
2888.
Minguzzi, E.
2013.
Convexity and quasi-uniformizability of closed preordered spaces.
Topology and its Applications,
Vol. 160,
Issue. 8,
p.
965.

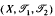 is quasi-metrizable if and only if for each point
is quasi-metrizable if and only if for each point 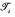 nbd bases {
nbd bases { 