No CrossRef data available.
Article contents
Commutative subsemigroups of the composition semigroup of formal power series over an integral domain
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let R be a commutative ring with identity. R[[x]] denotes the ring of formal power series, in which we consider the composition ○, defined by f(x)○g(x)=f(g(x)). This operation is well defined in the subring R+[[x]] of formal power series of positive order. The algebra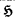
= 〈R+[[x]], ○〉 is learly a semigroup, which is not commutative for ∣R∣>1. In this paper we consider all those commutative subsemigroups of 
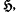, which consist of power series of all positive orders, which are called ‘permutable chains’.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1979
References
Baker, J. N. (1961–1962), ‘Permutable power series and regular iteration’, J. Australian Math. Soc. 2, 265–294.CrossRefGoogle Scholar
Gradstkeyn, J. S. and Ryzhik, J. M. (1965), Table of integrals, series and products (Academic Press, New York).Google Scholar
Kautschitsch, H. (1970), ‘Kommutative Teilhalbgruppen der Kompositionshalbgruppe von Polynomen und formalen Potenzreihen’, Monatsh. f. Math. 74, 421–436.CrossRefGoogle Scholar
Lausch, H. and Nöbauer, W. (1973), Algebra of polynomials (North-Holland Mathematical Library, Vol. 5, Amsterdam and London).Google Scholar
You have
Access