Although there is no need for a ‘distinguished’ submodule to be given a formal definition in the present paper, we like to indicate the meaning attached to this concept here. Perhaps the shortest way of doing so is to say that a distinguished submodule is a (covariant idempotent) functor from the category of (left) R-modules into itself mapping each R-module into its R-submodule specified by a family of left ideals of R. If 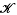is a family left ideals of R, then all elements of an R-module M of orders belonging to 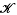, do not, of course, in general form a submodule of M; but, there are certain families 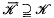such that all the elements of orders from 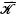form a submodule in any R-module (distinguished submodules defined by 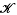). Consequently, no particular structural properties of the R-module are involved in the definition of such submodules. In this way we can define radicals (in the sense of Kuroš [4]) of a module. In particular, we feel that an application of this method is an appropriate way in defining the (maximal) torsion submodule of a module.