Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Maiyer, F. F.
Tastanov, M. G.
Utemissova, A. A.
and
Baimankulov, A. Т.
2024.
CLASSES OF CLOSE-TO-STARLIKE FUNCTIONS BASED ON THE REFERENCE FUNCTION OF A GENERAL FORM.
Herald of the Kazakh-British technical university,
Vol. 21,
Issue. 4,
p.
168.

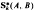 and the radius of convexity for
and the radius of convexity for 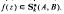 .
.