Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-04T19:00:05.026Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral bases of dihedral numberfields. I

Published online by Cambridge University Press:  09 April 2009

Walter Ledermann  and
Carol Van Der Ploeg
Walter Ledermann
Affiliation:
Mathematics Division University of SussexFalmer, Brighton, United Kingdom
Carol Van Der Ploeg
Affiliation:
London School of EconomicsLondon, England, United Kingdom
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A dihedral number field is a non-normal quartic field K which possesses a quadratic subfield k. That is, 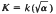for some integer α of k. Integral bases of these fields were known by Sommer (1907), but the form in which they were known was of little use for computational purposes. In this paper we construct integral bases of those dihedral fields with quadratic subfield of the form 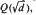, d ≢ 1 (mod 8), for which only rational quantities need be determined. Although the general theory may easily be generalized to the case d ≡ 1 (mod 8), the actual determination of integral bases in this case is left to a later paper.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 38 , Issue 3 , June 1985 , pp. 351 - 371
Copyright
Copyright © Australian Mathematical Society 1985

References

Berwick, W. E. H. (1927), Integral bases, Cambridge.Google Scholar
Hilbert, D. (1897), ‘Die Theorie der algebraischen Zahikörper’, Jber. Deutsch. Math.- Verein. 4, 175–546.Google Scholar
Mann, H. (1955), Introduction to algebraic number theory, Ohio State University Press.Google Scholar
Sommer, J. (1907), Introduction a la théorie des nombres algébriques, ParisGoogle Scholar