An interchange ring, 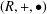$(R,+,\bullet )$ , is an abelian group with a second binary operation defined so that the interchange law 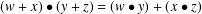$(w+x)\bullet (y+z)=(w\bullet y)+(x\bullet z)$ holds. An interchange near ring is the same structure based on a group which may not be abelian. It is shown that each interchange (near) ring based on a group 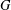$G$ is formed from a pair of endomorphisms of 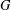$G$ whose images commute, and that all interchange (near) rings based on 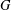$G$ can be characterized in this manner. To obtain an associative interchange ring, the endomorphisms must be commuting idempotents in the endomorphism semigroup of $G$ . For 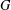$G$ a finite abelian group, we develop a group-theoretic analogue of the simultaneous diagonalization of idempotent linear operators and show that pairs of endomorphisms which yield associative interchange rings can be diagonalized and then put into a canonical form. A best possible upper bound of 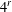$4^{r}$ can be given for the number of distinct isomorphism classes of associative interchange rings based on a finite abelian group 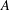$A$ which is a direct sum of $r$ cyclic groups of prime power order. If 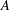$A$ is a direct sum of $r$ copies of the same cyclic group of prime power order, we show that there are exactly 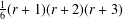${\textstyle \frac{1}{6}}(r+1)(r+2)(r+3)$ distinct isomorphism classes of associative interchange rings based on 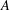$A$ . Several examples are given and further comments are made about the general theory of interchange rings.