Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pakes, Anthony G.
2008.
Tails of Stopped Random Products: The Factoid and Some Relatives.
Journal of Applied Probability,
Vol. 45,
Issue. 4,
p.
1161.
Pakes, Anthony G.
2008.
Tails of Stopped Random Products: The Factoid and Some Relatives.
Journal of Applied Probability,
Vol. 45,
Issue. 04,
p.
1161.
Watanabe, Toshiro
and
Yamamuro, Kouji
2010.
Ratio of the Tail of an Infinitely Divisible Distribution on the Line to that of its Lévy Measure.
Electronic Journal of Probability,
Vol. 15,
Issue. none,
LIU, YAN
and
TANG, QIHE
2010.
THE SUBEXPONENTIAL PRODUCT CONVOLUTION OF TWO WEIBULL-TYPE DISTRIBUTIONS.
Journal of the Australian Mathematical Society,
Vol. 89,
Issue. 2,
p.
277.
Leipus, Remigijus
and
Šiaulys, Jonas
2012.
Closure of some heavy-tailed distribution classes under random convolution*.
Lithuanian Mathematical Journal,
Vol. 52,
Issue. 3,
p.
249.
Gao, Qingwu
Liu, Yu
Psarrakos, Georgios
and
Wang, Yuebao
2013.
On asymptotic equivalence among the solutions of some defective renewal equations.
Lithuanian Mathematical Journal,
Vol. 53,
Issue. 4,
p.
391.
Yang, Yang
and
Gao, Qingwu
2014.
On closure properties of heavy-tailed distributions for random sums*.
Lithuanian Mathematical Journal,
Vol. 54,
Issue. 3,
p.
366.
Xu, Hui
Foss, Sergey
and
Wang, Yuebao
2015.
Convolution and convolution-root properties of long-tailed distributions.
Extremes,
Vol. 18,
Issue. 4,
p.
605.
Danilenko, Svetlana
and
Šiaulys, Jonas
2016.
Randomly stopped sums of not identically distributed heavy tailed random variables.
Statistics & Probability Letters,
Vol. 113,
Issue. ,
p.
84.
Andrulytė, Ieva Marija
Manstavičius, Martynas
and
Šiaulys, Jonas
2017.
Randomly stopped maximum and maximum of sums with consistently varying distributions.
Modern Stochastics: Theory and Applications,
Vol. 4,
Issue. 1,
p.
65.
Leipus, Remigijus
and
Šiaulys, Jonas
2017.
On the random max-closure for heavy-tailed random variables.
Lithuanian Mathematical Journal,
Vol. 57,
Issue. 2,
p.
208.
Danilenko, Svetlana
Šiaulys, Jonas
and
Stepanauskas, Gediminas
2018.
Closure properties of O-exponential distributions.
Statistics & Probability Letters,
Vol. 140,
Issue. ,
p.
63.
Ragulina, Olena
and
Šiaulys, Jonas
2019.
Randomly stopped minima and maxima with exponential-type distributions.
Nonlinear Analysis: Modelling and Control,
Vol. 24,
Issue. 2,
p.
297.
Wang, Shijie
Guo, Duo
and
Wang, Wensheng
2019.
Closure property of consistently varying random variables based on precise large deviation principles.
Communications in Statistics - Theory and Methods,
Vol. 48,
Issue. 9,
p.
2218.
Leipus, Remigijus
Šiaulys, Jonas
and
Konstantinides, Dimitrios
2023.
Closure Properties for Heavy-Tailed and Related Distributions.
p.
7.

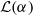 under convolution power mixtures (random summation).
under convolution power mixtures (random summation).