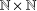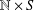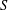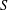Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Clayton, Ashley
2020.
On finitary properties for fiber products of free semigroups and free monoids.
Semigroup Forum,
Vol. 101,
Issue. 2,
p.
326.
East, James
and
Ham, Nicholas
2021.
Lattice Paths and Submonoids of $$\mathbb Z^2$$.
Annals of Combinatorics,
Vol. 25,
Issue. 4,
p.
797.
East, James
2022.
Presentations for $${\mathbb {P}}^K$$.
Monatshefte für Mathematik,
Vol. 197,
Issue. 2,
p.
293.
Ruškuc, Nik
and
Witt, Bill de
2023.
On the number of countable subdirect powers of unary algebras.
International Journal of Algebra and Computation,
Vol. 33,
Issue. 06,
p.
1183.
CLAYTON, ASHLEY
REILLY, CATHERINE
and
RUŠKUC, NIK
2025.
A CHARACTERISATION OF SEMIGROUPS WITH ONLY COUNTABLY MANY SUBDIRECT PRODUCTS WITH
$\mathbb {Z}$
.
Bulletin of the Australian Mathematical Society,
Vol. 111,
Issue. 2,
p.
314.