Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-12T18:04:17.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Projective characters of degree one and the inflation-restriction sequence

Part of: Representation theory of groups

Published online by Cambridge University Press:  09 April 2009

R. J. Higgs
R. J. Higgs
Affiliation:
Department of Mathematics, University College Dublin, Belfield Dublin 4, Ireland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a finite group, α be a fixed cocycle of G and Proj (G, α) denote the set of irreducible projective characters of G lying over the cocycle α.

Suppose N is a normal subgroup of G. Then the author shows that there exists a G- invariant element of Proj(N, αN) of degree 1 if and only if [α] is an element of the image of the inflation homomorphism from M(G/N) into M(G), where M(G) denotes the Schur multiplier of G. However in many situations one can produce such G-invariant characters where it is not intrinsically obvious that the cocycle could be inflated. Because of this the author obtains a restatement of his original result using the Lyndon-Hochschild-Serre exact sequence of cohomology. This restatement not only resolves the apparent anomalies, but also yields as a corollary the well-known fact that the inflation-restriction sequence 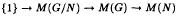is exact when N is perfect.

Keywords

projective representations of finite groups.

MSC classification

Secondary: 20C25: Projective representations and multipliers
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 46 , Issue 2 , April 1989 , pp. 272 - 280
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Haggarty, R. J. and Humphreys, J. F., ‘Projective characters of finite groups’, Proc. London Math. Soc. (3) 36 (1978), 176–192.CrossRefGoogle Scholar
[2]Isaacs, I. M., Character theory of finite groups (Pure and Applied Mathematics, a Series of Monographs and Textbooks 69, Academic Press, New York, London, 1976).Google Scholar
[3]Karpilovsky, G., Projective representations of finite groups (Monographs and Textbooks in Pure and Applied Mathematics 94, Marcel Dekker, New York, 1985).Google Scholar
[4]Liebler, R. A. and Yellen, J. E., ‘In search of nonsolvable groups of central type’, Pacific J. Math. 82 (1979) 485–492.CrossRefGoogle Scholar
[5]Macdonald, I. D., ‘Commutators and their products’, Amer. Math. Monthly 93 (1986), 440–443.CrossRefGoogle Scholar
[6]Lane, S. Mac, Homology (Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen 114, Springer-Verlag, Berlin, Heidelberg, New York, 1967).Google Scholar
[7]Mangold, Ruth, ‘Beitrage zur Theorie der Darstellungen endlicher Gruppen durch Kollineationen’, Mitt. Math. Sem. Giessen 69 (1966), 1–44.Google Scholar