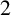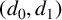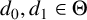1 Introduction
In this document, topological groups are second-countable, locally compact groups are Hausdorff and the word ‘representation’ stands for a strongly continuous unitary representation on a separable complex Hilbert space. A locally compact group G is called CCR if the operator
![]() $\pi (f)$
is compact for all irreducible representations
$\pi (f)$
is compact for all irreducible representations
![]() $\pi $
of G and all
$\pi $
of G and all
![]() $f\in L^{1}(G)$
. For totally disconnected locally compact groups, this property is equivalent to the requirement that every irreducible representation of G is admissible; see [Reference NebbiaNeb99]. We recall that an irreducible representation
$f\in L^{1}(G)$
. For totally disconnected locally compact groups, this property is equivalent to the requirement that every irreducible representation of G is admissible; see [Reference NebbiaNeb99]. We recall that an irreducible representation
![]() $\pi $
of a totally disconnected locally compact group G is admissible if for every compact open subgroup
$\pi $
of a totally disconnected locally compact group G is admissible if for every compact open subgroup
![]() $K \leq G$
, the space
$K \leq G$
, the space
![]() $\mathcal {H}_{\pi }^K$
of K-invariant vectors is finite dimensional. A very important property of CCR groups is that they are type I groups [Reference Bekka and de la HarpeBdlH20, Definition 6.E.7. and Proposition 6.E.11]. Loosely speaking, type I groups are the locally compact groups all of whose representations can be written as unique direct integrals of irreducible representations, thus reducing the study of arbitrary representations to considerations of irreducible representations. Concerning groups of automorphisms of trees, Nebbia’s work highlighted surprising relations between the action on the boundary and the regularity of representation theory. To be more precise, he showed in [Reference NebbiaNeb99] that any closed unimodular CCR vertex-transitive subgroup
$\mathcal {H}_{\pi }^K$
of K-invariant vectors is finite dimensional. A very important property of CCR groups is that they are type I groups [Reference Bekka and de la HarpeBdlH20, Definition 6.E.7. and Proposition 6.E.11]. Loosely speaking, type I groups are the locally compact groups all of whose representations can be written as unique direct integrals of irreducible representations, thus reducing the study of arbitrary representations to considerations of irreducible representations. Concerning groups of automorphisms of trees, Nebbia’s work highlighted surprising relations between the action on the boundary and the regularity of representation theory. To be more precise, he showed in [Reference NebbiaNeb99] that any closed unimodular CCR vertex-transitive subgroup
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
of the group of automorphisms of a regular tree T necessarily acts transitively on the boundary
$G\leq \operatorname {\mathrm {Aut}}(T)$
of the group of automorphisms of a regular tree T necessarily acts transitively on the boundary
![]() $\partial T$
. Further progress going in that direction was recently achieved by Houdayer and Raum [Reference Houdayer and RaumHR19] and, at a higher level of generality, by Caprace et al. [Reference Caprace, Kalantar and MonodCKM23]. Among other things, they showed that a closed nonamenable type I subgroup acting minimally on a locally finite tree T acts
$\partial T$
. Further progress going in that direction was recently achieved by Houdayer and Raum [Reference Houdayer and RaumHR19] and, at a higher level of generality, by Caprace et al. [Reference Caprace, Kalantar and MonodCKM23]. Among other things, they showed that a closed nonamenable type I subgroup acting minimally on a locally finite tree T acts
![]() $2$
-transitively on the boundary
$2$
-transitively on the boundary
![]() $\partial T$
[Reference Caprace, Kalantar and MonodCKM23, Corollary D]. Going in the other direction, Nebbia conjectured in [Reference NebbiaNeb99] that any closed subgroup of automorphisms of a regular tree acting transitively on the boundary is CCR. His conjecture naturally extends to the case of semi-regular trees.
$\partial T$
[Reference Caprace, Kalantar and MonodCKM23, Corollary D]. Going in the other direction, Nebbia conjectured in [Reference NebbiaNeb99] that any closed subgroup of automorphisms of a regular tree acting transitively on the boundary is CCR. His conjecture naturally extends to the case of semi-regular trees.
Conjecture (CCR conjecture on trees [Reference NebbiaNeb99]).
Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 3$
and let
$d_0,d_1\geq 3$
and let
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
be a closed subgroup acting transitively on the boundary of T. Then G is CCR.
$G\leq \operatorname {\mathrm {Aut}}(T)$
be a closed subgroup acting transitively on the boundary of T. Then G is CCR.
We recall from [Reference Burger and MozesBM00, Lemma 3.1.1] that, for a locally finite tree T, closed subgroups
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
are noncompact and act transitively on the boundary
$G\leq \operatorname {\mathrm {Aut}}(T)$
are noncompact and act transitively on the boundary
![]() $\partial T$
if and only if they act
$\partial T$
if and only if they act
![]() $2$
-transitively on
$2$
-transitively on
![]() $\partial T$
. Furthermore, the existence of such a group implies that the tree is semi-regular. In particular, since compact groups are automatically CCR, the hypothesis of semi-regularity is not restrictive in the conjecture.
$\partial T$
. Furthermore, the existence of such a group implies that the tree is semi-regular. In particular, since compact groups are automatically CCR, the hypothesis of semi-regularity is not restrictive in the conjecture.
One of the first pieces of evidence supporting the conjecture was provided by Bernstein and Harish-Chandra’s works. Among other things, they proved that rank one semi-simple algebraic groups over local-fields are uniformly admissible [Reference BernšteĭnBer74, HC70]. We recall that a totally disconnected locally compact group G is uniformly admissible if for every compact open subgroup K, there exists a positive integer
![]() $k_K$
such that
$k_K$
such that
![]() ${\dim (\mathcal {H}_{\pi }^K)<k_K}$
for all irreducible representations
${\dim (\mathcal {H}_{\pi }^K)<k_K}$
for all irreducible representations
![]() $\pi $
of G. In particular, uniformly admissible groups are CCR. Concerning nonlinear groups, the conjecture was supported by the complete classification of the irreducible representations of the full group of automorphisms of a semi-regular tree and more generally of closed subgroups acting transitively on the boundary and satisfying the Tits independence property [Reference AmannAma03, Reference ChoucrounCho94, Reference Figà-Talamanca and NebbiaFTN91, Reference Ol’shanskiiOl’77, Reference Ol’shanskiiOl’82] (these classifications lead to the conclusion that they are uniformly admissible [Reference CiobotaruCio15]).
$\pi $
of G. In particular, uniformly admissible groups are CCR. Concerning nonlinear groups, the conjecture was supported by the complete classification of the irreducible representations of the full group of automorphisms of a semi-regular tree and more generally of closed subgroups acting transitively on the boundary and satisfying the Tits independence property [Reference AmannAma03, Reference ChoucrounCho94, Reference Figà-Talamanca and NebbiaFTN91, Reference Ol’shanskiiOl’77, Reference Ol’shanskiiOl’82] (these classifications lead to the conclusion that they are uniformly admissible [Reference CiobotaruCio15]).
Our paper concerns closed subgroups acting
![]() $2$
-transitively on the boundary
$2$
-transitively on the boundary
![]() $\partial T$
and whose local action at each vertex v contains the alternating group of corresponding degree. We recall that for each vertex
$\partial T$
and whose local action at each vertex v contains the alternating group of corresponding degree. We recall that for each vertex
![]() $v\in V(T)$
, the stabiliser
$v\in V(T)$
, the stabiliser
![]() $\mathrm {Fix}_G(v)$
of v acts on the set
$\mathrm {Fix}_G(v)$
of v acts on the set
![]() $E(v)$
of edges containing v. The image of
$E(v)$
of edges containing v. The image of
![]() $\mathrm {Fix}_G(v)$
in
$\mathrm {Fix}_G(v)$
in
![]() $\operatorname {\mathrm {Sym}}(E(v))$
for this natural projection map is called the local action of G at v and we denote this group by
$\operatorname {\mathrm {Sym}}(E(v))$
for this natural projection map is called the local action of G at v and we denote this group by
![]() $\underline {G}(v)$
. When the degree of each vertex is greater than
$\underline {G}(v)$
. When the degree of each vertex is greater than
![]() $6$
, these groups of automorphisms of trees have been extensively studied and classified by Radu in [Reference RaduRad17]. For this reason, we call them Radu groups. It is not hard to realise that these groups are type I. Indeed, each Radu group G contains a cocompact subgroup H that is conjugate in
$6$
, these groups of automorphisms of trees have been extensively studied and classified by Radu in [Reference RaduRad17]. For this reason, we call them Radu groups. It is not hard to realise that these groups are type I. Indeed, each Radu group G contains a cocompact subgroup H that is conjugate in
![]() $\operatorname {\mathrm {Aut}}(T)$
to the semi-regular version of the universal group of Burger–Mozes
$\operatorname {\mathrm {Aut}}(T)$
to the semi-regular version of the universal group of Burger–Mozes
![]() $\operatorname {\mathrm {Alt}}_{(i)}(T)^+$
; see [Reference RaduRad17, page 4]. Since H is both open and cocompact in G, [Reference KallmanKal70, Theorem 1] ensures that G is type I if and only if H is type I. However, when the degree of each vertex is greater than
$\operatorname {\mathrm {Alt}}_{(i)}(T)^+$
; see [Reference RaduRad17, page 4]. Since H is both open and cocompact in G, [Reference KallmanKal70, Theorem 1] ensures that G is type I if and only if H is type I. However, when the degree of each vertex is greater than
![]() $4$
,
$4$
,
![]() $\operatorname {\mathrm {Alt}}_{(i)}(T)^+$
acts transitively on the boundary and satisfies the Tits independence property. It follows from [Reference AmannAma03, Reference CiobotaruCio15] that H is a type I group, which proves that every Radu group is type I. The purpose of these notes is to go further. Inspired by Ol’shanskii’s work and the recent progress achieved on the abstraction of his framework [Reference SemalSem23], we give a classification of the irreducible representations of simple Radu groups and deduce a description of the irreducible representations of any Radu group. Among other things, we provide the following contribution to Nebbia’s CCR conjecture.
$\operatorname {\mathrm {Alt}}_{(i)}(T)^+$
acts transitively on the boundary and satisfies the Tits independence property. It follows from [Reference AmannAma03, Reference CiobotaruCio15] that H is a type I group, which proves that every Radu group is type I. The purpose of these notes is to go further. Inspired by Ol’shanskii’s work and the recent progress achieved on the abstraction of his framework [Reference SemalSem23], we give a classification of the irreducible representations of simple Radu groups and deduce a description of the irreducible representations of any Radu group. Among other things, we provide the following contribution to Nebbia’s CCR conjecture.
Theorem A. Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 6$
. Then, Radu groups are uniformly admissible and hence CCR.
$d_0,d_1\geq 6$
. Then, Radu groups are uniformly admissible and hence CCR.
To put this result into the perspective of Radu’s paper, we recall that the local action
![]() $\underline {G}(v)\leq \operatorname {\mathrm {Sym}}(E(v))$
at every vertex
$\underline {G}(v)\leq \operatorname {\mathrm {Sym}}(E(v))$
at every vertex
![]() $v\in T$
of a closed subgroup
$v\in T$
of a closed subgroup
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
that is
$G\leq \operatorname {\mathrm {Aut}}(T)$
that is
![]() $2$
-transitive on the boundary is a
$2$
-transitive on the boundary is a
![]() $2$
-transitive subgroup of
$2$
-transitive subgroup of
![]() $\operatorname {\mathrm {Sym}}(E(v))$
[Reference Burger and MozesBM00, Lemma 3.1.1]. However, [Reference RaduRad17, Proposition B.1 and Corollary B.2] ensure that
$\operatorname {\mathrm {Sym}}(E(v))$
[Reference Burger and MozesBM00, Lemma 3.1.1]. However, [Reference RaduRad17, Proposition B.1 and Corollary B.2] ensure that
is asymptotically dense in
![]() $\mathbb N$
and its ten smallest elements are
$\mathbb N$
and its ten smallest elements are
![]() $34$
,
$34$
,
![]() $35$
,
$35$
,
![]() $39$
,
$39$
,
![]() $45$
,
$45$
,
![]() $46$
,
$46$
,
![]() $51$
,
$51$
,
![]() $52$
,
$52$
,
![]() $55$
,
$55$
,
![]() $56$
and
$56$
and
![]() $58$
. All together, this implies the following.
$58$
. All together, this implies the following.
Theorem B. Nebbia’s CCR conjecture on trees is confirmed for any
![]() $(d_0,d_1)$
-semi- regular tree with
$(d_0,d_1)$
-semi- regular tree with
![]() $d_0,d_1\in \Theta $
where
$d_0,d_1\in \Theta $
where
![]() $\Theta $
is the asymptotically dense subset of
$\Theta $
is the asymptotically dense subset of
![]() $\mathbb N$
defined above.
$\mathbb N$
defined above.
We now come back to the classification of the irreducible representations of simple Radu groups. We recall that the irreducible representations of a closed automorphism group
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
of a locally finite tree T split into three categories. An irreducible representation
$G\leq \operatorname {\mathrm {Aut}}(T)$
of a locally finite tree T split into three categories. An irreducible representation
![]() $\pi $
of G is called:
$\pi $
of G is called:
-
• spherical if there exists a vertex
 $v\in V(T)$
such that
$v\in V(T)$
such that
 $\pi $
admits a nonzero
$\pi $
admits a nonzero
 $\mathrm {Fix}_G(v)$
-invariant vector where
$\mathrm {Fix}_G(v)$
-invariant vector where
 $\mathrm {Fix}_G(v)=\{g\in G\mid gv=v\}$
;
$\mathrm {Fix}_G(v)=\{g\in G\mid gv=v\}$
; -
• special if it is not spherical and there exists an edge
 $e\in E(T)$
such that
$e\in E(T)$
such that
 $\pi $
admits a nonzero
$\pi $
admits a nonzero
 $\mathrm {Fix}_G(e)$
-invariant vector where
$\mathrm {Fix}_G(e)$
-invariant vector where
 $\mathrm {Fix}_G(e)=\{g\in G\mid gv=v\,\text { for all } v\in e\}$
is the fixator of the edge e;
$\mathrm {Fix}_G(e)=\{g\in G\mid gv=v\,\text { for all } v\in e\}$
is the fixator of the edge e; -
• cuspidal if for every
 $e \in E(T)$
,
$e \in E(T)$
,
 $\pi $
does not admit a nonzero
$\pi $
does not admit a nonzero
 $\mathrm {Fix}_G(e)$
-invariant vector.
$\mathrm {Fix}_G(e)$
-invariant vector.
The spherical and special representations are classified since the end of the 1970s at the level of generality of the conjecture, that is, for any closed noncompact subgroup
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
acting transitively on the boundary of the tree; see [Reference MatsumotoMat77, Reference Ol’shanskiiOl’77, Reference Ol’shanskiiOl’82]. Furthermore, we recall that Matsumoto’s work emphasises a strong connection between these kinds of representations and the irreducible representations of Hecke algebras. To be more precise, we recall that a group acting
$G\leq \operatorname {\mathrm {Aut}}(T)$
acting transitively on the boundary of the tree; see [Reference MatsumotoMat77, Reference Ol’shanskiiOl’77, Reference Ol’shanskiiOl’82]. Furthermore, we recall that Matsumoto’s work emphasises a strong connection between these kinds of representations and the irreducible representations of Hecke algebras. To be more precise, we recall that a group acting
![]() $2$
-transitively on the boundary is either type-preserving or admits a closed type-preserving subgroup of index
$2$
-transitively on the boundary is either type-preserving or admits a closed type-preserving subgroup of index
![]() $2$
acting
$2$
acting
![]() $2$
-transitively on the boundary. Since [Reference Caprace and CiobotaruCC15, Corollary 3.6] ensures that every closed type-preserving subgroup G acting
$2$
-transitively on the boundary. Since [Reference Caprace and CiobotaruCC15, Corollary 3.6] ensures that every closed type-preserving subgroup G acting
![]() $2$
-transitively on the boundary comes from a B–N pair, every spherical and every special representation of G also provide an irreducible representation of the associated Hecke algebra
$2$
-transitively on the boundary comes from a B–N pair, every spherical and every special representation of G also provide an irreducible representation of the associated Hecke algebra
![]() $C_c(B\backslash G/ B)$
of continuous compactly supported B-bi-invariant functions
$C_c(B\backslash G/ B)$
of continuous compactly supported B-bi-invariant functions
![]() $f:G\rightarrow \mathbb C$
, where
$f:G\rightarrow \mathbb C$
, where
![]() ${B=\mathrm {Fix}_G(e)}$
is the pointwise fixator of an edge
${B=\mathrm {Fix}_G(e)}$
is the pointwise fixator of an edge
![]() $e\in E(T)$
. Matsumoto’s works revealed that this correspondence is actually bijective; see [Reference MatsumotoMat77, Ch. 5, Section 6].
$e\in E(T)$
. Matsumoto’s works revealed that this correspondence is actually bijective; see [Reference MatsumotoMat77, Ch. 5, Section 6].
The cuspidal representations, however, are not classified at the level of generality of the conjecture. Nevertheless, a classification of the cuspidal representations was achieved for certain families of groups. Concerning nonlinear groups, Ol’shanskii obtained such a classification for any closed subgroup
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
satisfying the Tits independence property by exploiting the independence of the action on the tree to deduce a particular factorisation of the compact open subgroups; see [Reference AmannAma03, Reference Ol’shanskiiOl’77]. Our paper takes advantage of the recent abstraction of his framework given by the notion of Ol’shanskii’s factorisation (see [Reference SemalSem23] or Definition 4.3 below) and the description of Radu groups [Reference RaduRad17] to obtain a classification for their cuspidal representations. We start by considering a family of groups
$G\leq \operatorname {\mathrm {Aut}}(T)$
satisfying the Tits independence property by exploiting the independence of the action on the tree to deduce a particular factorisation of the compact open subgroups; see [Reference AmannAma03, Reference Ol’shanskiiOl’77]. Our paper takes advantage of the recent abstraction of his framework given by the notion of Ol’shanskii’s factorisation (see [Reference SemalSem23] or Definition 4.3 below) and the description of Radu groups [Reference RaduRad17] to obtain a classification for their cuspidal representations. We start by considering a family of groups
![]() $G_{(i)}^+(Y_0,Y_1)$
indexed by finite subsets
$G_{(i)}^+(Y_0,Y_1)$
indexed by finite subsets
![]() $Y_0,Y_1\subseteq \mathbb N$
; see Definition 3.3. It is shown in [Reference RaduRad17] that these groups are abstractly simple when T is a
$Y_0,Y_1\subseteq \mathbb N$
; see Definition 3.3. It is shown in [Reference RaduRad17] that these groups are abstractly simple when T is a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 4$
and that they exhaust the list of simple Radu groups when
$d_0,d_1\geq 4$
and that they exhaust the list of simple Radu groups when
![]() $d_0,d_1\geq 6$
. Furthermore, by exploiting the fact that these groups are determined by suitable local conditions, [Reference SemalSem23] leads to the following result.
$d_0,d_1\geq 6$
. Furthermore, by exploiting the fact that these groups are determined by suitable local conditions, [Reference SemalSem23] leads to the following result.
Theorem C. Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 4$
. The cuspidal representations of
$d_0,d_1\geq 4$
. The cuspidal representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
are in bijective correspondence given by induction with a family of irreducible representations of compact open subgroups. This correspondence is explicitly given by Theorem 4.12.
$G_{(i)}^+(Y_0,Y_1)$
are in bijective correspondence given by induction with a family of irreducible representations of compact open subgroups. This correspondence is explicitly given by Theorem 4.12.
Among other things, this theorem proves that the cuspidal representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
are square-integrable. In the light of [HC70, Corollary of Theorem 2] and of the classification of spherical and special representations recalled in Section 2, this proves that the groups
$G_{(i)}^+(Y_0,Y_1)$
are square-integrable. In the light of [HC70, Corollary of Theorem 2] and of the classification of spherical and special representations recalled in Section 2, this proves that the groups
![]() $G_{(i)}^+(Y_0,Y_1)$
are uniformly admissible, and hence CCR (the details are gathered in Section 5). To put these results into the perspective of Radu’s classification, we recall that every Radu group G belongs to a finite chain
$G_{(i)}^+(Y_0,Y_1)$
are uniformly admissible, and hence CCR (the details are gathered in Section 5). To put these results into the perspective of Radu’s classification, we recall that every Radu group G belongs to a finite chain
![]() ${H_n\geq \cdots \geq H_0}$
with
${H_n\geq \cdots \geq H_0}$
with
![]() $n\in \{0,1,2,3\}$
such that
$n\in \{0,1,2,3\}$
such that
![]() $H_n=G$
,
$H_n=G$
,
![]() $\lbrack H_t: H_{t-1} \rbrack =2$
for all t and
$\lbrack H_t: H_{t-1} \rbrack =2$
for all t and
![]() $H_0$
is conjugate in the group of type-preserving automorphisms
$H_0$
is conjugate in the group of type-preserving automorphisms
![]() $\operatorname {\mathrm {Aut}}(T)^+$
to one of these
$\operatorname {\mathrm {Aut}}(T)^+$
to one of these
![]() $G_{(i)}^+(Y_0,Y_1)$
when
$G_{(i)}^+(Y_0,Y_1)$
when
![]() $d_0,d_1\geq 6$
. However, Mackey’s machinery allows one to describe the irreducible representation of a locally compact G in terms of the irreducible representations of any of its closed subgroups of index
$d_0,d_1\geq 6$
. However, Mackey’s machinery allows one to describe the irreducible representation of a locally compact G in terms of the irreducible representations of any of its closed subgroups of index
![]() $2$
. In particular, when
$2$
. In particular, when
![]() $d_0,d_1\geq 6$
, we obtain a description of the cuspidal representations of any Radu group from the cuspidal representations of the groups
$d_0,d_1\geq 6$
, we obtain a description of the cuspidal representations of any Radu group from the cuspidal representations of the groups
![]() $G_{(i)}^+(Y_0,Y_1)$
. We also deduce from Mackey’s machinery that every Radu group is uniformly admissible. The author would like to underline that an application of Ol’shanskii’s framework to Radu groups is already presented in [Reference SemalSem23, Section 4] since these groups satisfy a generalisation of the Tits independence property (the property
$G_{(i)}^+(Y_0,Y_1)$
. We also deduce from Mackey’s machinery that every Radu group is uniformly admissible. The author would like to underline that an application of Ol’shanskii’s framework to Radu groups is already presented in [Reference SemalSem23, Section 4] since these groups satisfy a generalisation of the Tits independence property (the property
![]() $\mathrm {IP} _k$
introduced in [Reference Banks, Elder and WillisBEW15]). However, except when the property
$\mathrm {IP} _k$
introduced in [Reference Banks, Elder and WillisBEW15]). However, except when the property
![]() $\mathrm {IP} _k$
is the Tits independence property (
$\mathrm {IP} _k$
is the Tits independence property (
![]() $k=1$
), the approach adopted in [Reference SemalSem23] never leads to a classification of all the cuspidal representations.
$k=1$
), the approach adopted in [Reference SemalSem23] never leads to a classification of all the cuspidal representations.
1.1 Structure of the paper
In Section 2, we recall the classification of spherical and special representations of any closed noncompact subgroup
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
acting transitively on the boundary; see [Reference MatsumotoMat77, Reference Ol’shanskiiOl’77, Reference Ol’shanskiiOl’82]. The purpose of Section 3 is to recall Radu’s classification of Radu groups [Reference RaduRad17] and the definition of
$G\leq \operatorname {\mathrm {Aut}}(T)$
acting transitively on the boundary; see [Reference MatsumotoMat77, Reference Ol’shanskiiOl’77, Reference Ol’shanskiiOl’82]. The purpose of Section 3 is to recall Radu’s classification of Radu groups [Reference RaduRad17] and the definition of
![]() $G_{(i)}^+(Y_0,Y_1)$
. In Section 4, we recall the notion of Ol’shanskii’s factorisation developed in [Reference SemalSem23] and obtain a classification of the cuspidal representations of
$G_{(i)}^+(Y_0,Y_1)$
. In Section 4, we recall the notion of Ol’shanskii’s factorisation developed in [Reference SemalSem23] and obtain a classification of the cuspidal representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
. The complete classification of the irreducible representations of
$G_{(i)}^+(Y_0,Y_1)$
. The complete classification of the irreducible representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
resulting from Sections 2 and 4 is then used in Section 5 to prove uniform admissibility. Finally, the purpose of the Appendix is to recall the details of the correspondence given by Mackey’s machinery between the irreducible representations of a locally compact G and the irreducible representations of any of its closed subgroups of index
$G_{(i)}^+(Y_0,Y_1)$
resulting from Sections 2 and 4 is then used in Section 5 to prove uniform admissibility. Finally, the purpose of the Appendix is to recall the details of the correspondence given by Mackey’s machinery between the irreducible representations of a locally compact G and the irreducible representations of any of its closed subgroups of index
![]() $2$
. In particular, the Appendix provides a way to obtain the irreducible representations of any Radu group from the irreducible representations of the abstractly simple Radu groups
$2$
. In particular, the Appendix provides a way to obtain the irreducible representations of any Radu group from the irreducible representations of the abstractly simple Radu groups
![]() $G_{(i)}^+(Y_0,Y_1)$
. We also deduce from the Appendix that all Radu groups are uniformly admissible when
$G_{(i)}^+(Y_0,Y_1)$
. We also deduce from the Appendix that all Radu groups are uniformly admissible when
![]() $d_0,d_1 \geq 6$
.
$d_0,d_1 \geq 6$
.
2 Spherical and special representations
Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 3$
. We recall that a tree T is called
$d_0,d_1\geq 3$
. We recall that a tree T is called
![]() $(d_0,d_1)$
-semi-regular if there exists a bipartition
$(d_0,d_1)$
-semi-regular if there exists a bipartition
![]() $V(T)=V_0\sqcup V_1$
of T such that every vertex of
$V(T)=V_0\sqcup V_1$
of T such that every vertex of
![]() $V_i$
has degree
$V_i$
has degree
![]() $d_i$
and every edge of T contains exactly one vertex in each
$d_i$
and every edge of T contains exactly one vertex in each
![]() $V_i$
. As explained in Section 1, the irreducible representations of any closed subgroup
$V_i$
. As explained in Section 1, the irreducible representations of any closed subgroup
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
of the group of automorphisms of such a tree split into three categories. These representations are either spherical, special or cuspidal. The purpose of the present section is to recall the classification of spherical and special representations of any closed noncompact subgroup
$G\leq \operatorname {\mathrm {Aut}}(T)$
of the group of automorphisms of such a tree split into three categories. These representations are either spherical, special or cuspidal. The purpose of the present section is to recall the classification of spherical and special representations of any closed noncompact subgroup
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
acting transitively on the boundary (in particular of any Radu group). This classification is a classical result known since the end of the 70’s and we claim no originality. We refer to [Reference MatsumotoMat77, Reference Ol’shanskiiOl’77, Reference Figà-Talamanca and NebbiaFTN91] for details.
$G\leq \operatorname {\mathrm {Aut}}(T)$
acting transitively on the boundary (in particular of any Radu group). This classification is a classical result known since the end of the 70’s and we claim no originality. We refer to [Reference MatsumotoMat77, Reference Ol’shanskiiOl’77, Reference Figà-Talamanca and NebbiaFTN91] for details.
The details of this classification are gathered in Theorems 2.2, 2.3, 2.5 below but we start with some preliminaries. Given a locally compact group G and a compact subgroup
![]() $K\leq G$
, we say that
$K\leq G$
, we say that
![]() $(G, K)$
is a Gelfand pair if the convolution algebra
$(G, K)$
is a Gelfand pair if the convolution algebra
![]() $C_c(K \backslash G / K)$
of compactly supported, continuous K-bi-invariant functions on G is commutative. Let
$C_c(K \backslash G / K)$
of compactly supported, continuous K-bi-invariant functions on G is commutative. Let
![]() $(G,K)$
be a Gelfand pair and let
$(G,K)$
be a Gelfand pair and let
![]() $\mu $
be the left-Haar measure of G renormalised so that
$\mu $
be the left-Haar measure of G renormalised so that
![]() $\mu (K)=1$
. A function
$\mu (K)=1$
. A function
![]() $\varphi : G\rightarrow \mathbb C$
is called K
-spherical if it is a K-bi-invariant continuous function with
$\varphi : G\rightarrow \mathbb C$
is called K
-spherical if it is a K-bi-invariant continuous function with
![]() $\varphi (1_G)=1$
and such that
$\varphi (1_G)=1$
and such that
Theorem 2.1 [Reference LangLan85, Ch. IV, Section 3, Theorems
 $3$
and
$3$
and
 $9$
].
$9$
].
Let
![]() $(G,K)$
be a Gelfand pair. For every irreducible representation
$(G,K)$
be a Gelfand pair. For every irreducible representation
![]() $\pi $
of G we have that
$\pi $
of G we have that
![]() $\dim (\mathcal {H}_{\pi }^K)\leq 1$
. Furthermore, there is a bijective correspondence
$\dim (\mathcal {H}_{\pi }^K)\leq 1$
. Furthermore, there is a bijective correspondence
![]() $\pi \rightarrow \varphi _\pi $
with inverse map given by the GNS construction between the equivalence classes of irreducible representations of G with nonzero K-invariant vectors and the K-spherical functions of positive type on G (the function
$\pi \rightarrow \varphi _\pi $
with inverse map given by the GNS construction between the equivalence classes of irreducible representations of G with nonzero K-invariant vectors and the K-spherical functions of positive type on G (the function
![]() $\varphi _\pi $
is the function
$\varphi _\pi $
is the function
![]() $\varphi _{\pi }(g)=\langle \pi (g)\xi ,\xi \rangle $
corresponding to any unit vector
$\varphi _{\pi }(g)=\langle \pi (g)\xi ,\xi \rangle $
corresponding to any unit vector
![]() $\xi \in \mathcal {H}_{\pi }^K$
).
$\xi \in \mathcal {H}_{\pi }^K$
).
We now recall the details of the classification of spherical and special representations for any noncompact closed subgroup
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
acting transitively on the boundary of T. We recall that these groups have either one or two orbits of vertices and we treat these cases separately.
$G\leq \operatorname {\mathrm {Aut}}(T)$
acting transitively on the boundary of T. We recall that these groups have either one or two orbits of vertices and we treat these cases separately.
Theorem 2.2 [Reference Figà-Talamanca and NebbiaFTN91, Ch. II].
Let T be a d-regular tree, let
![]() $v\in V(T)$
and let
$v\in V(T)$
and let
![]() ${G\leq \operatorname {\mathrm {Aut}}(T)}$
be a closed noncompact subgroup acting transitively on the vertices of T and the boundary
${G\leq \operatorname {\mathrm {Aut}}(T)}$
be a closed noncompact subgroup acting transitively on the vertices of T and the boundary
![]() $\partial T$
. Then,
$\partial T$
. Then,
![]() $(G, \mathrm {Fix}_G(v))$
is a Gelfand pair and every spherical representation of G admits a nonzero
$(G, \mathrm {Fix}_G(v))$
is a Gelfand pair and every spherical representation of G admits a nonzero
![]() $\mathrm {Fix}_G(v)$
-invariant vector. Furthermore, the equivalence classes of spherical representations of G are in bijective correspondence with the interval
$\mathrm {Fix}_G(v)$
-invariant vector. Furthermore, the equivalence classes of spherical representations of G are in bijective correspondence with the interval
![]() $\lbrack -1; 1\rbrack $
via the map
$\lbrack -1; 1\rbrack $
via the map
![]() $\phi _v:\pi \mapsto \varphi _\pi (\tau _v)$
where
$\phi _v:\pi \mapsto \varphi _\pi (\tau _v)$
where
![]() $\tau _v$
is any element of G such that
$\tau _v$
is any element of G such that
![]() $d(\tau _v v,v)=1$
and
$d(\tau _v v,v)=1$
and
![]() $\varphi _\pi $
is the unique
$\varphi _\pi $
is the unique
![]() $\mathrm {Fix}_G(v)$
-spherical function of positive type attached with
$\mathrm {Fix}_G(v)$
-spherical function of positive type attached with
![]() $\pi $
. Under this correspondence, the trivial representation corresponds to
$\pi $
. Under this correspondence, the trivial representation corresponds to
![]() $1$
.
$1$
.
The following theorem comes from [Reference MatsumotoMat77] but is formulated differently for the sake of consistency.
Theorem 2.3 [Reference MatsumotoMat77, Ch. 5, Section 6].
Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 3$
, let
$d_0,d_1\geq 3$
, let
![]() $v\in V(T)$
, let
$v\in V(T)$
, let
![]() $v'$
be any vertex at distance one from v and let
$v'$
be any vertex at distance one from v and let
![]() ${G\leq \operatorname {\mathrm {Aut}}(T)^+}$
be a closed noncompact subgroup of type-preserving automorphisms acting transitively on the boundary
${G\leq \operatorname {\mathrm {Aut}}(T)^+}$
be a closed noncompact subgroup of type-preserving automorphisms acting transitively on the boundary
![]() $\partial T$
. Then, there is exactly one spherical representation
$\partial T$
. Then, there is exactly one spherical representation
![]() $\pi _v$
of G with a nonzero
$\pi _v$
of G with a nonzero
![]() $\mathrm {Fix}_G(v)$
-invariant vector but no nonzero
$\mathrm {Fix}_G(v)$
-invariant vector but no nonzero
![]() $\mathrm {Fix}_G(v')$
-invariant vector. Furthermore,
$\mathrm {Fix}_G(v')$
-invariant vector. Furthermore,
![]() $(G, \mathrm {Fix}_G(v))$
is a Gelfand pair and apart from the two exceptional representations
$(G, \mathrm {Fix}_G(v))$
is a Gelfand pair and apart from the two exceptional representations
![]() $\pi _v$
and
$\pi _v$
and
![]() $\pi _{v'}$
, every spherical representation of G admits a nonzero
$\pi _{v'}$
, every spherical representation of G admits a nonzero
![]() $\mathrm {Fix}_G(w)$
-invariant vector for all
$\mathrm {Fix}_G(w)$
-invariant vector for all
![]() $w\in V(T)$
. In addition, the equivalence classes of spherical representations admitting a nonzero
$w\in V(T)$
. In addition, the equivalence classes of spherical representations admitting a nonzero
![]() $\mathrm {Fix}_G(v)$
-invariant vector are in bijective correspondence with the interval
$\mathrm {Fix}_G(v)$
-invariant vector are in bijective correspondence with the interval
![]() $\lbrack -{1}/({d'-1});1\rbrack $
via the map
$\lbrack -{1}/({d'-1});1\rbrack $
via the map
![]() $\phi _v:\pi \mapsto \varphi _\pi (\tau _v)$
where
$\phi _v:\pi \mapsto \varphi _\pi (\tau _v)$
where
![]() $\tau _v$
is an element of G such that
$\tau _v$
is an element of G such that
![]() $d(\tau _v v,v)=2$
and
$d(\tau _v v,v)=2$
and
![]() $d'$
is the degree of
$d'$
is the degree of
![]() $v'$
. Under this correspondence, the exceptional spherical representation
$v'$
. Under this correspondence, the exceptional spherical representation
![]() $\pi _v$
corresponds to
$\pi _v$
corresponds to
![]() $-{1}/({d'-1})$
and the trivial representation corresponds to
$-{1}/({d'-1})$
and the trivial representation corresponds to
![]() $1$
. Finally, if
$1$
. Finally, if
![]() $\pi $
is a nonexceptional spherical representation of G,
$\pi $
is a nonexceptional spherical representation of G,
Remark 2.4. The author wishes to point out that certain extrema of the real interval corresponding to spherical functions of positive types found in the literature are incorrect when G has two orbits of vertices. The incorrect values provided by [Reference AmannAma03, Reference Bouaziz-KellilBK88] for instance are based on earlier inaccuracies [Reference Iozzi, Picardello, Mauceri, Ricci and WeissIP83] that were already pointed out in [Reference Cartwright, Młotkowski and StegerCMoS94, Remark
![]() $2$
, page
$2$
, page
![]() $243$
]. The values provided in Theorem 2.3 can be computed from [Reference MatsumotoMat69].
$243$
]. The values provided in Theorem 2.3 can be computed from [Reference MatsumotoMat69].
To describe the special representations, let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 3$
, let
$d_0,d_1\geq 3$
, let
![]() $e\in E(T)$
and let
$e\in E(T)$
and let
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
be an edge-transitive closed subgroup acting transitively on the boundary
$G\leq \operatorname {\mathrm {Aut}}(T)$
be an edge-transitive closed subgroup acting transitively on the boundary
![]() $\partial T$
. We define
$\partial T$
. We define
![]() $\mathcal {L}(e)$
as the subspace of
$\mathcal {L}(e)$
as the subspace of
![]() $\mathrm {Fix}_{G}(e)$
-right invariant square-integrable functions
$\mathrm {Fix}_{G}(e)$
-right invariant square-integrable functions
![]() $\varphi : G \rightarrow \mathbb C$
satisfying
$\varphi : G \rightarrow \mathbb C$
satisfying
 $$ \begin{align*} \int_{\mathrm{Fix}_G(v)}\varphi(gk)\,d \mu(k)=0\quad \forall g\in G \quad\forall v\in e. \end{align*} $$
$$ \begin{align*} \int_{\mathrm{Fix}_G(v)}\varphi(gk)\,d \mu(k)=0\quad \forall g\in G \quad\forall v\in e. \end{align*} $$
Notice that
![]() $\mathcal {L}(e)$
is a closed left-invariant subspace of
$\mathcal {L}(e)$
is a closed left-invariant subspace of
![]() $L^2(G)$
and let
$L^2(G)$
and let
![]() $\sigma $
be the unitary representation of G defined by
$\sigma $
be the unitary representation of G defined by
![]() $\sigma (t)\varphi (g)=\varphi (t^{-1}g)$
for all
$\sigma (t)\varphi (g)=\varphi (t^{-1}g)$
for all
![]() $g,t\in G$
, for all
$g,t\in G$
, for all
![]() $\varphi \in \mathcal {L}(e)$
. If G is transitive on the vertices of T, we choose an inversion
$\varphi \in \mathcal {L}(e)$
. If G is transitive on the vertices of T, we choose an inversion
![]() $h\in G$
of the edge e and consider the linear map
$h\in G$
of the edge e and consider the linear map
![]() $\nu :\mathcal {L}(e) \rightarrow \mathcal {L}(e)$
defined by
$\nu :\mathcal {L}(e) \rightarrow \mathcal {L}(e)$
defined by
![]() $\nu (\varphi )(g)=\varphi (gh)$
for all
$\nu (\varphi )(g)=\varphi (gh)$
for all
![]() $\varphi \in \mathcal {L}(e)$
, for all
$\varphi \in \mathcal {L}(e)$
, for all
![]() $g\in G$
. This map is well defined since for all
$g\in G$
. This map is well defined since for all
![]() $\varphi \in \mathcal {L}(e)$
, for all
$\varphi \in \mathcal {L}(e)$
, for all
![]() $g\in G$
, for all
$g\in G$
, for all
![]() $v\in e$
,
$v\in e$
,
 $$ \begin{align*} \int_{\mathrm{Fix}_G(v)} (\nu\varphi)(gk)\,d \mu(k)&=\int_{\mathrm{Fix}_G(v)} \varphi(gkh)\,d \mu(k)\\ &=\int_{\mathrm{Fix}_G(v)} \varphi(ghh^{-1}kh)\,d \mu(k)\\ &=\int_{\mathrm{Fix}_G(h^{-1}v)} \varphi(ghk)\,d \mu(k)=0. \end{align*} $$
$$ \begin{align*} \int_{\mathrm{Fix}_G(v)} (\nu\varphi)(gk)\,d \mu(k)&=\int_{\mathrm{Fix}_G(v)} \varphi(gkh)\,d \mu(k)\\ &=\int_{\mathrm{Fix}_G(v)} \varphi(ghh^{-1}kh)\,d \mu(k)\\ &=\int_{\mathrm{Fix}_G(h^{-1}v)} \varphi(ghk)\,d \mu(k)=0. \end{align*} $$
On the other hand, since every element of
![]() $\mathcal {L}(e)$
is
$\mathcal {L}(e)$
is
![]() $\mathrm {Fix}_G(e)$
-right invariant, note that
$\mathrm {Fix}_G(e)$
-right invariant, note that
![]() $\nu $
is an involution and that it does not depend on our choice of inversion of the edge e. For each
$\nu $
is an involution and that it does not depend on our choice of inversion of the edge e. For each
![]() $\epsilon \in \{-1,1\}$
, let
$\epsilon \in \{-1,1\}$
, let
![]() $\mathcal {L}(e)_{\epsilon }$
be the eigenspace of
$\mathcal {L}(e)_{\epsilon }$
be the eigenspace of
![]() $\nu $
corresponding to the eigenvalue
$\nu $
corresponding to the eigenvalue
![]() $\epsilon $
and let
$\epsilon $
and let
![]() $\sigma ^\epsilon $
be the restriction of
$\sigma ^\epsilon $
be the restriction of
![]() $\sigma $
to
$\sigma $
to
![]() $\mathcal {L}(e)_{\epsilon }$
. We are now ready to state the classification of special representations.
$\mathcal {L}(e)_{\epsilon }$
. We are now ready to state the classification of special representations.
Theorem 2.5 [Reference Figà-Talamanca and NebbiaFTN91, Ch. III, Section 2], [Reference MatsumotoMat77, Section 5.6].
Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 3$
, let
$d_0,d_1\geq 3$
, let
![]() $e\in E(T)$
and let
$e\in E(T)$
and let
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
be a closed noncompact subgroup acting transitively on the boundary
$G\leq \operatorname {\mathrm {Aut}}(T)$
be a closed noncompact subgroup acting transitively on the boundary
![]() $\partial T$
. Every special representation of G is square-integrable and admits a
$\partial T$
. Every special representation of G is square-integrable and admits a
![]() $\mathrm {Fix}_G(f)$
-invariant vector for every
$\mathrm {Fix}_G(f)$
-invariant vector for every
![]() $f\in E(T)$
. Furthermore:
$f\in E(T)$
. Furthermore:
-
(1) If G acts transitively on
 $V(T)$
,
$V(T)$
,
 $(\sigma ^{-1},\mathcal {L}(e)_{-1})$
and
$(\sigma ^{-1},\mathcal {L}(e)_{-1})$
and
 $(\sigma ^{+1},\mathcal {L}(e)_{+1})$
are representatives of the two equivalence classes of special representations.
$(\sigma ^{+1},\mathcal {L}(e)_{+1})$
are representatives of the two equivalence classes of special representations. -
(2) If G has two orbits on
 $V(T)$
,
$V(T)$
,
 $(\sigma ,\mathcal {L}(e))$
is a representative of the unique equivalence class of special representations.
$(\sigma ,\mathcal {L}(e))$
is a representative of the unique equivalence class of special representations.
3 The Radu groups
Let T be a
![]() $(d_0,d_1)$
semi-regular tree with
$(d_0,d_1)$
semi-regular tree with
![]() $d_0,d_1\geq 4$
and associated bipartition
$d_0,d_1\geq 4$
and associated bipartition
![]() $V(T)=V_0\sqcup V_1$
, and let
$V(T)=V_0\sqcup V_1$
, and let
![]() $\operatorname {\mathrm {Aut}}(T)^+$
denote the group of type-preserving automorphisms of T that is the set of automorphisms of T leaving
$\operatorname {\mathrm {Aut}}(T)^+$
denote the group of type-preserving automorphisms of T that is the set of automorphisms of T leaving
![]() $V_0$
and
$V_0$
and
![]() $V_1$
invariants. The purpose of this section is to recall the classification of Radu groups [Reference RaduRad17]. For this purpose, we set
$V_1$
invariants. The purpose of this section is to recall the classification of Radu groups [Reference RaduRad17]. For this purpose, we set
and
If
![]() $d_0 \not = d_1$
, notice that every automorphism of T is type-preserving, so
$d_0 \not = d_1$
, notice that every automorphism of T is type-preserving, so
![]() $\mathcal {H}_T^+= \mathcal {H}_T$
. We recall that for each vertex
$\mathcal {H}_T^+= \mathcal {H}_T$
. We recall that for each vertex
![]() $v\in V(T)$
, the stabiliser
$v\in V(T)$
, the stabiliser
![]() $\mathrm {Fix}_G(v)$
of v acts on the set
$\mathrm {Fix}_G(v)$
of v acts on the set
![]() $E(v)$
of edges containing v, and that the image of
$E(v)$
of edges containing v, and that the image of
![]() $\mathrm {Fix}_G(v)$
in
$\mathrm {Fix}_G(v)$
in
![]() $\operatorname {\mathrm {Sym}}(E(v))$
for this projection map (which we denote by
$\operatorname {\mathrm {Sym}}(E(v))$
for this projection map (which we denote by
![]() $\underline {G}(v)$
) is called the local action of G at v. Furthermore, we recall in the light of [Reference Burger and MozesBM00, Lemma 3.1.1], that every group
$\underline {G}(v)$
) is called the local action of G at v. Furthermore, we recall in the light of [Reference Burger and MozesBM00, Lemma 3.1.1], that every group
![]() $G\in \mathcal {H}_T^+$
is transitive on
$G\in \mathcal {H}_T^+$
is transitive on
![]() $V_0$
and
$V_0$
and
![]() $V_1$
. Thus, all the groups
$V_1$
. Thus, all the groups
![]() $\underline {G}(v)$
with
$\underline {G}(v)$
with
![]() $v\in V_0$
(respectively
$v\in V_0$
(respectively
![]() $v\in V_1$
) are permutation isomorphic to the same group
$v\in V_1$
) are permutation isomorphic to the same group
![]() $F_0\leq \operatorname {\mathrm {Sym}}(d_0)$
(respectively
$F_0\leq \operatorname {\mathrm {Sym}}(d_0)$
(respectively
![]() $F_1\leq \operatorname {\mathrm {Sym}}(d_1)$
). A group
$F_1\leq \operatorname {\mathrm {Sym}}(d_1)$
). A group
![]() $G\in \mathcal {H}_T$
such that
$G\in \mathcal {H}_T$
such that
![]() $\underline {G}(v)\cong F_t\geq \operatorname {\mathrm {Alt}}(d_t)$
for each vertex
$\underline {G}(v)\cong F_t\geq \operatorname {\mathrm {Alt}}(d_t)$
for each vertex
![]() $v\in V_t(T)$
and for
$v\in V_t(T)$
and for
![]() $t\in \{0,1\}$
is called a Radu group. For each vertex
$t\in \{0,1\}$
is called a Radu group. For each vertex
![]() $v\in V(T)$
and each positive integer
$v\in V(T)$
and each positive integer
![]() $r\in \mathbb N$
let
$r\in \mathbb N$
let
be the set of vertices of T at distance r from v.
Definition 3.1. A legal colouring
![]() $i:V(T)\rightarrow \mathbb N$
of T is the concatenation of a pair of maps
$i:V(T)\rightarrow \mathbb N$
of T is the concatenation of a pair of maps
such that ![]() are bijections for all
are bijections for all
![]() $v\in V_1$
and
$v\in V_1$
and
![]() $w\in V_0$
.
$w\in V_0$
.
Given a legal colouring i of T and an automorphism
![]() $g\in \operatorname {\mathrm {Aut}}(T)$
, the local action of g at a vertex
$g\in \operatorname {\mathrm {Aut}}(T)$
, the local action of g at a vertex
![]() $v\in V(T)$
is defined as
$v\in V(T)$
is defined as

Remark 3.2. If
![]() $d_0=d_1$
, the tree T is a regular tree and this notion of legal colouring and local action of an element is different from the notion of legal colouring and local action used to define the universal Burger–Mozes groups in [Reference Burger and MozesBM00]. Indeed, with our definition, the closed subgroup
$d_0=d_1$
, the tree T is a regular tree and this notion of legal colouring and local action of an element is different from the notion of legal colouring and local action used to define the universal Burger–Mozes groups in [Reference Burger and MozesBM00]. Indeed, with our definition, the closed subgroup
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
of all automorphisms of trees
$G\leq \operatorname {\mathrm {Aut}}(T)$
of all automorphisms of trees
![]() $g\in G$
such that
$g\in G$
such that
![]() $\sigma _{(i)}(g,v)=\operatorname {\mathrm {id}} \text { for all } v\in V$
is not transitive on the set of vertices of T (not even transitive on
$\sigma _{(i)}(g,v)=\operatorname {\mathrm {id}} \text { for all } v\in V$
is not transitive on the set of vertices of T (not even transitive on
![]() $V_0$
). It is good to note, however, that this colouring approach is compatible with that of Smith [Reference SmithSmi17].
$V_0$
). It is good to note, however, that this colouring approach is compatible with that of Smith [Reference SmithSmi17].
Now, let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 4$
and let i be a legal colouring of T. For each vertex
$d_0,d_1\geq 4$
and let i be a legal colouring of T. For each vertex
![]() $v\in V(T)$
and each finite set
$v\in V(T)$
and each finite set
![]() $Y\subseteq \mathbb N$
let
$Y\subseteq \mathbb N$
let
and for each set of vertices
![]() $B\subseteq V(T)$
let
$B\subseteq V(T)$
let
where
![]() $\operatorname {\mathrm {sgn}}(\sigma _{(i)}(g,w))$
is the sign of the local action
$\operatorname {\mathrm {sgn}}(\sigma _{(i)}(g,w))$
is the sign of the local action
![]() $\sigma _{(i)}(g,w)$
of the automorphism g at w for the legal colouring i.
$\sigma _{(i)}(g,w)$
of the automorphism g at w for the legal colouring i.
Definition 3.3. For all (possibly empty) finite sets
![]() $Y_0, Y_1$
of
$Y_0, Y_1$
of
![]() $\mathbb N$
and every legal colouring i of T, we set
$\mathbb N$
and every legal colouring i of T, we set
 $$ \begin{align*} G^+_{(i)}(Y_0,Y_1)=\left\{g\in \operatorname{\mathrm{Aut}}(T)^+\ \middle\vert\,\kern0.1pt \begin{array}{@{}l@{}} \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_0}(v))=1 \mbox{ for each }v\in V_{t_0}\\ \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_1}(v))=1 \mbox{ for each }v\in V_{t_1} \end{array}\right\}, \end{align*} $$
$$ \begin{align*} G^+_{(i)}(Y_0,Y_1)=\left\{g\in \operatorname{\mathrm{Aut}}(T)^+\ \middle\vert\,\kern0.1pt \begin{array}{@{}l@{}} \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_0}(v))=1 \mbox{ for each }v\in V_{t_0}\\ \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_1}(v))=1 \mbox{ for each }v\in V_{t_1} \end{array}\right\}, \end{align*} $$
where
![]() $t_0=\max (Y_0)\ \pmod{\,2}$
,
$t_0=\max (Y_0)\ \pmod{\,2}$
,
![]() $t_1=(1+\max (Y_1))\ \pmod{\,2}$
and
$t_1=(1+\max (Y_1))\ \pmod{\,2}$
and
![]() $\max (\varnothing )=0$
.
$\max (\varnothing )=0$
.
Remark 3.4. The choices of
![]() $t_0$
and
$t_0$
and
![]() $t_1$
are made in such a way that the vertices of
$t_1$
are made in such a way that the vertices of
![]() $S_{Y_0}(v)$
with
$S_{Y_0}(v)$
with
![]() $v\in V_{t_0}$
at maximal distance from v and the vertices of
$v\in V_{t_0}$
at maximal distance from v and the vertices of
![]() $S_{Y_1}(w)$
with
$S_{Y_1}(w)$
with
![]() $w\in V_{t_1}$
at maximal distance from w have opposite types.
$w\in V_{t_1}$
at maximal distance from w have opposite types.
Note that
![]() $G_{(i)}^+(\varnothing ,\varnothing )=\operatorname {\mathrm {Aut}}(T)^+$
is the full group of type-preserving automorphisms and that
$G_{(i)}^+(\varnothing ,\varnothing )=\operatorname {\mathrm {Aut}}(T)^+$
is the full group of type-preserving automorphisms and that
![]() $G^+_{(i)}(\{0\},\{0\})$
is a subgroup of each
$G^+_{(i)}(\{0\},\{0\})$
is a subgroup of each
![]() $G^+_{(i)}(Y_0,Y_1)$
. Furthermore, if T is a d-regular tree note that
$G^+_{(i)}(Y_0,Y_1)$
. Furthermore, if T is a d-regular tree note that
![]() $G^+_{(i)}(\{0\},\{0\})$
is conjugate to
$G^+_{(i)}(\{0\},\{0\})$
is conjugate to
![]() $U(\operatorname {\mathrm {Alt}}(d))^+$
where
$U(\operatorname {\mathrm {Alt}}(d))^+$
where
![]() $G^+=G\cap \operatorname {\mathrm {Aut}}(T)^+$
and
$G^+=G\cap \operatorname {\mathrm {Aut}}(T)^+$
and
![]() $U(\operatorname {\mathrm {Alt}}(d))$
is the universal Burger–Mozes group of the alternating group see [Reference Burger and MozesBM00]. As we recall below, when
$U(\operatorname {\mathrm {Alt}}(d))$
is the universal Burger–Mozes group of the alternating group see [Reference Burger and MozesBM00]. As we recall below, when
![]() $d_0,d_1\geq 6$
, every simple Radu group is of the form
$d_0,d_1\geq 6$
, every simple Radu group is of the form
![]() $G_{(i)}^+(Y_0,Y_1)$
for some finite
$G_{(i)}^+(Y_0,Y_1)$
for some finite
![]() $Y_0,Y_1\subseteq \mathbb N$
and some legal colouring i of T. Furthermore, every Radu group G belongs to a finite chain
$Y_0,Y_1\subseteq \mathbb N$
and some legal colouring i of T. Furthermore, every Radu group G belongs to a finite chain
![]() $H_n\geq \cdots \geq H_0$
with
$H_n\geq \cdots \geq H_0$
with
![]() $n\in \{0,1,2,3\}$
such that
$n\in \{0,1,2,3\}$
such that
![]() $H_n=G$
,
$H_n=G$
,
![]() $\lbrack H_t: H_{t-1} \rbrack =2$
for all t and
$\lbrack H_t: H_{t-1} \rbrack =2$
for all t and
![]() $H_0$
is conjugate in
$H_0$
is conjugate in
![]() $\operatorname {\mathrm {Aut}}(T)^+$
to one of these
$\operatorname {\mathrm {Aut}}(T)^+$
to one of these
![]() $G_{(i)}^+(Y_0,Y_1)$
. In particular, Mackey’s machinery (see the Appendix) allows one to obtain a description of the irreducible representations of any Radu group from the irreducible representations of
$G_{(i)}^+(Y_0,Y_1)$
. In particular, Mackey’s machinery (see the Appendix) allows one to obtain a description of the irreducible representations of any Radu group from the irreducible representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
and vice versa. We now recall more precisely the results proved in [Reference RaduRad17] that are used in this paper.
$G_{(i)}^+(Y_0,Y_1)$
and vice versa. We now recall more precisely the results proved in [Reference RaduRad17] that are used in this paper.
Theorem [Reference RaduRad17, Theorem A].
Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 4$
and let i be a legal colouring of T. Then, for all finite subsets
$d_0,d_1\geq 4$
and let i be a legal colouring of T. Then, for all finite subsets
![]() $Y_0, Y_1\subseteq \mathbb N$
the group
$Y_0, Y_1\subseteq \mathbb N$
the group
![]() $G^+_{(i)}(Y_0,Y_1)$
belongs to
$G^+_{(i)}(Y_0,Y_1)$
belongs to
![]() $\mathcal {H}^+_T$
and is abstractly simple.
$\mathcal {H}^+_T$
and is abstractly simple.
To formulate the following results we let
![]() $G^{(\infty )}$
denote the intersection of all normal cocompact closed subgroups of the locally compact group G. Furthermore, we recall from [Reference Burger and MozesBM00, Proposition 3.1.2] that
$G^{(\infty )}$
denote the intersection of all normal cocompact closed subgroups of the locally compact group G. Furthermore, we recall from [Reference Burger and MozesBM00, Proposition 3.1.2] that
![]() $H^{(\infty )}$
belongs to
$H^{(\infty )}$
belongs to
![]() $\mathcal {H}^+_T$
and is topologically simple for all
$\mathcal {H}^+_T$
and is topologically simple for all
![]() $H\in \mathcal {H}^+_T$
(in our cases, these groups are even abstractly simple). Finally, we let
$H\in \mathcal {H}^+_T$
(in our cases, these groups are even abstractly simple). Finally, we let
![]() $\mathcal {G}_{T}^+(i)$
be the set of groups
$\mathcal {G}_{T}^+(i)$
be the set of groups
![]() $G^+_{i}(Y_0,Y_1)$
with nonempty finite
$G^+_{i}(Y_0,Y_1)$
with nonempty finite
![]() $Y_0, Y_1\subseteq \mathbb N$
such that
$Y_0, Y_1\subseteq \mathbb N$
such that
![]() $y=\max (Y_t)\ \pmod{\,2}$
for each
$y=\max (Y_t)\ \pmod{\,2}$
for each
![]() $y\in Y_t$
with
$y\in Y_t$
with
![]() $y\geq \max (Y_{1-t})$
(
$y\geq \max (Y_{1-t})$
(
![]() $t\in \{0,1\}$
).
$t\in \{0,1\}$
).
Theorem [Reference RaduRad17, Theorem B].
Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 6$
, let i be a legal colouring, and let
$d_0,d_1\geq 6$
, let i be a legal colouring, and let
![]() $G\in \mathcal {H}^+_T$
be such that
$G\in \mathcal {H}^+_T$
be such that
![]() $\underline {G}(v)\cong F_0\geq \operatorname {\mathrm {Alt}}(d_0)$
and
$\underline {G}(v)\cong F_0\geq \operatorname {\mathrm {Alt}}(d_0)$
and
![]() ${\underline {G}(w)\cong F_1\geq \operatorname {\mathrm {Alt}}(d_1)}$
for each
${\underline {G}(w)\cong F_1\geq \operatorname {\mathrm {Alt}}(d_1)}$
for each
![]() $v\in V_0$
,
$v\in V_0$
,
![]() $w\in V_1$
. Then,
$w\in V_1$
. Then,
![]() $G^{(\infty )}$
is conjugate in
$G^{(\infty )}$
is conjugate in
![]() $\operatorname {\mathrm {Aut}}(T)^+$
to an element of
$\operatorname {\mathrm {Aut}}(T)^+$
to an element of
![]() $\mathcal {G}_{T}^+(i)$
and
$\mathcal {G}_{T}^+(i)$
and
![]() $\lbrack G: G^{(\infty )}\rbrack \in \{1,2,4\}$
.
$\lbrack G: G^{(\infty )}\rbrack \in \{1,2,4\}$
.
When T is a d-regular tree, a similar result holds for all
![]() $G\in \mathcal {H}_T- \mathcal {H}_T^+$
.
$G\in \mathcal {H}_T- \mathcal {H}_T^+$
.
Theorem [Reference RaduRad17, Corollary C].
Let T be a d-regular tree with
![]() $d\geq 6$
and let i be a legal colouring and let
$d\geq 6$
and let i be a legal colouring and let
![]() $G\in \mathcal {H}_{T}- \mathcal {H}^+_T$
be such that
$G\in \mathcal {H}_{T}- \mathcal {H}^+_T$
be such that
![]() $\underline {G}(v)\cong F\geq \operatorname {\mathrm {Alt}}(d)$
for each
$\underline {G}(v)\cong F\geq \operatorname {\mathrm {Alt}}(d)$
for each
![]() $v\in V(T)$
. Then,
$v\in V(T)$
. Then,
![]() $G^{(\infty )}$
is conjugate to
$G^{(\infty )}$
is conjugate to
![]() ${G}^+_{(i)}(Y,Y)$
for some finite subset Y of
${G}^+_{(i)}(Y,Y)$
for some finite subset Y of
![]() $\mathbb N$
and
$\mathbb N$
and
![]() ${\lbrack G: G^{(\infty )} \rbrack \in \{2,4,8\}}$
.
${\lbrack G: G^{(\infty )} \rbrack \in \{2,4,8\}}$
.
Finally, the following theorem follows from Radu’s description of Radu groups.
Theorem 3.5. Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 6$
and let i be a legal colouring of T. Every Radu group G is contained in a finite chain
$d_0,d_1\geq 6$
and let i be a legal colouring of T. Every Radu group G is contained in a finite chain
![]() $H_n\geq \cdots \geq H_0$
with
$H_n\geq \cdots \geq H_0$
with
![]() $n\in \{0,1,2,3\}$
such that
$n\in \{0,1,2,3\}$
such that
![]() $H_n=G$
,
$H_n=G$
,
![]() $\lbrack H_t: H_{t-1} \rbrack =2$
for all t and
$\lbrack H_t: H_{t-1} \rbrack =2$
for all t and
![]() $H_0$
is conjugate in
$H_0$
is conjugate in
![]() $\operatorname {\mathrm {Aut}}(T)^+$
to some
$\operatorname {\mathrm {Aut}}(T)^+$
to some
![]() $G_{(i)}^+(Y_0,Y_1)$
.
$G_{(i)}^+(Y_0,Y_1)$
.
4 Cuspidal representations of the simple Radu groups
Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 4$
and let
$d_0,d_1\geq 4$
and let
![]() $V(T)=V_0\sqcup V_1$
be the associated bipartition. Let i be a legal colouring of T and let
$V(T)=V_0\sqcup V_1$
be the associated bipartition. Let i be a legal colouring of T and let
![]() $Y_0,Y_1\subseteq \mathbb N$
be two finite subsets. We recall from Section 3 that
$Y_0,Y_1\subseteq \mathbb N$
be two finite subsets. We recall from Section 3 that
![]() $G_{(i)}^+(Y_0,Y_1)$
(Definition 3.3) is a simple Radu group and that every simple Radu group is of this form when
$G_{(i)}^+(Y_0,Y_1)$
(Definition 3.3) is a simple Radu group and that every simple Radu group is of this form when
![]() $d_0,d_1\geq 6$
. The purpose of this section is to describe the irreducible representations of
$d_0,d_1\geq 6$
. The purpose of this section is to describe the irreducible representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
and to show that this group is uniformly admissible, hence CCR.
$G_{(i)}^+(Y_0,Y_1)$
and to show that this group is uniformly admissible, hence CCR.
We recall from Section 1 that the irreducible representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
split into three categories. These are either spherical, special or cuspidal. A classification of the spherical and special representations of any subgroup
$G_{(i)}^+(Y_0,Y_1)$
split into three categories. These are either spherical, special or cuspidal. A classification of the spherical and special representations of any subgroup
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
acting
$G\leq \operatorname {\mathrm {Aut}}(T)$
acting
![]() $2$
-transitively on the boundary is already given in Section 2. In particular, this classification applies to
$2$
-transitively on the boundary is already given in Section 2. In particular, this classification applies to
![]() $G_{(i)}^+(Y_0,Y_1)$
. Our current purpose is to give a description of the cuspidal representations of these groups. As announced in Section 1, our idea is to take advantage of the framework developed in [Reference SemalSem23] and the description of these groups provided by Radu. The abstraction of Ol’shanskii’s framework expressed in [Reference SemalSem23, Theorem A] provides a way to classify the representations at certain ‘depths’ where the depth is a generalisation of the ‘spherical/special/cuspidal’ framework, that is, larger depth means that more compact open subgroups have no nonzero invariant vector. This framework as well as the associated notion of depth depends on the existence and choice (assuming the existence) of a basis of neighbourhoods of the identity satisfying a certain factorisation property. Such a basis is given in [Reference SemalSem23] for groups of automorphisms of trees satisfying the property
$G_{(i)}^+(Y_0,Y_1)$
. Our current purpose is to give a description of the cuspidal representations of these groups. As announced in Section 1, our idea is to take advantage of the framework developed in [Reference SemalSem23] and the description of these groups provided by Radu. The abstraction of Ol’shanskii’s framework expressed in [Reference SemalSem23, Theorem A] provides a way to classify the representations at certain ‘depths’ where the depth is a generalisation of the ‘spherical/special/cuspidal’ framework, that is, larger depth means that more compact open subgroups have no nonzero invariant vector. This framework as well as the associated notion of depth depends on the existence and choice (assuming the existence) of a basis of neighbourhoods of the identity satisfying a certain factorisation property. Such a basis is given in [Reference SemalSem23] for groups of automorphisms of trees satisfying the property
![]() $\mathrm {IP} _k$
as defined in [Reference Banks, Elder and WillisBEW15] and yielding to a classification of their cuspidal representations at sufficiently large depth depending on k. Since every Radu group G is known to satisfy the property
$\mathrm {IP} _k$
as defined in [Reference Banks, Elder and WillisBEW15] and yielding to a classification of their cuspidal representations at sufficiently large depth depending on k. Since every Radu group G is known to satisfy the property
![]() $\mathrm {IP} _k$
for some sufficiently large k depending on G, this classification applies to the Radu groups. However, this approach only leads to a description of all the cuspidal representations of
$\mathrm {IP} _k$
for some sufficiently large k depending on G, this classification applies to the Radu groups. However, this approach only leads to a description of all the cuspidal representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
when
$G_{(i)}^+(Y_0,Y_1)$
when
![]() $k=1$
, that is, when G satisfies the Tits independence property, because for that choice of basis of neighbourhoods of the identity, the set of the associated representations at depth
$k=1$
, that is, when G satisfies the Tits independence property, because for that choice of basis of neighbourhoods of the identity, the set of the associated representations at depth
![]() $0$
contains some cuspidal representations (increasingly many as k grows). The purpose of this section is to go beyond this result by exhibiting the basis of neighbourhoods of the identity of the group
$0$
contains some cuspidal representations (increasingly many as k grows). The purpose of this section is to go beyond this result by exhibiting the basis of neighbourhoods of the identity of the group
![]() $G_{(i)}^+(Y_0,Y_1)$
that satisfies the factorisation property at all positive depths, and whose associated representations at depth
$G_{(i)}^+(Y_0,Y_1)$
that satisfies the factorisation property at all positive depths, and whose associated representations at depth
![]() $0$
are exactly the spherical and special representations. This is done by relying on the local conditions given by the Definition 3.3 provided by Radu’s work rather than the property
$0$
are exactly the spherical and special representations. This is done by relying on the local conditions given by the Definition 3.3 provided by Radu’s work rather than the property
![]() $\mathrm {IP}_k$
and leads to a complete description of the cuspidal representations of
$\mathrm {IP}_k$
and leads to a complete description of the cuspidal representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
rather than a partial one; see Section 4.4.
$G_{(i)}^+(Y_0,Y_1)$
rather than a partial one; see Section 4.4.
4.1 Preliminaries
We start by recalling the axiomatic framework developed in [Reference SemalSem23] (see that paper for details). Let G be a unimodular totally disconnected locally compact group, let
![]() $\mathcal {B}$
denote the set of compact open subgroups of G,
$\mathcal {B}$
denote the set of compact open subgroups of G,
![]() $P(\mathcal {B})$
denote the power set of
$P(\mathcal {B})$
denote the power set of
![]() $\mathcal {B}$
and let
$\mathcal {B}$
and let
be the map sending a compact open subgroup to its conjugacy class in G. Let
![]() $\mathcal {S}$
be a basis of neighbourhoods of the identity consisting of compact open subgroups of G and let
$\mathcal {S}$
be a basis of neighbourhoods of the identity consisting of compact open subgroups of G and let
![]() $\mathcal {F}_{\mathcal {S}}=\{ \mathcal {C}(U)\mid U\in \mathcal {S}\}$
. We equip
$\mathcal {F}_{\mathcal {S}}=\{ \mathcal {C}(U)\mid U\in \mathcal {S}\}$
. We equip
![]() $\mathcal {F}_{\mathcal {S}}$
with the partial order given by the reverse inclusion of representatives (
$\mathcal {F}_{\mathcal {S}}$
with the partial order given by the reverse inclusion of representatives (
![]() $\mathcal {C}(U)\leq \mathcal {C}(V)$
if there exists
$\mathcal {C}(U)\leq \mathcal {C}(V)$
if there exists
![]() $\tilde {U}\in \mathcal {C}(U)$
and
$\tilde {U}\in \mathcal {C}(U)$
and
![]() $\tilde {V}\in \mathcal {C}(V)$
such that
$\tilde {V}\in \mathcal {C}(V)$
such that
![]() $\tilde {V}\subseteq \tilde {U}$
). For a poset
$\tilde {V}\subseteq \tilde {U}$
). For a poset
![]() $(P, \leq )$
and an element
$(P, \leq )$
and an element
![]() $x\in P$
, we recall that the height of x in
$x\in P$
, we recall that the height of x in
![]() $(P,\leq )$
is
$(P,\leq )$
is
![]() $L_x-1$
, where
$L_x-1$
, where
![]() $L_x$
is the maximal length of a strictly increasing chain in
$L_x$
is the maximal length of a strictly increasing chain in
![]() $P_{\leq x}=\{y\in P\mid y\leq x\}$
if such a maximal length exists and we say that the height is infinite otherwise.
$P_{\leq x}=\{y\in P\mid y\leq x\}$
if such a maximal length exists and we say that the height is infinite otherwise.
Definition 4.1. A basis of neighbourhoods of the identity
![]() $\mathcal {S}$
consisting of compact open subgroups of G is called a generic filtration of G if the height of every element in
$\mathcal {S}$
consisting of compact open subgroups of G is called a generic filtration of G if the height of every element in
![]() $\mathcal {F}_{\mathcal {S}}$
is finite.
$\mathcal {F}_{\mathcal {S}}$
is finite.
Remark 4.2. Every unimodular totally disconnected locally compact group has a generic filtration, namely the compact open subgroups U with
![]() $\mu (U)\leq 1$
for some Haar measure
$\mu (U)\leq 1$
for some Haar measure
![]() $\mu $
.
$\mu $
.
Every generic filtration
![]() $\mathcal {S}$
of G splits as a disjoint union
$\mathcal {S}$
of G splits as a disjoint union
![]() $\mathcal {S}=\bigsqcup _{l\in \mathbb N}\mathcal {S}\lbrack l \rbrack $
, where
$\mathcal {S}=\bigsqcup _{l\in \mathbb N}\mathcal {S}\lbrack l \rbrack $
, where
![]() $\mathcal {S}\lbrack l\rbrack $
denotes the set of elements
$\mathcal {S}\lbrack l\rbrack $
denotes the set of elements
![]() $U\in \mathcal {S}$
such that
$U\in \mathcal {S}$
such that
![]() $\mathcal {C}(U)$
has height l in
$\mathcal {C}(U)$
has height l in
![]() $\mathcal {F}_{\mathcal {S}}$
. The elements of
$\mathcal {F}_{\mathcal {S}}$
. The elements of
![]() $\mathcal {S}\lbrack l \rbrack $
are called the elements at depth l. Since
$\mathcal {S}\lbrack l \rbrack $
are called the elements at depth l. Since
![]() $\mathcal {S}$
is a basis of neighbourhoods of the identity consisting of compact open subgroups of G, notice that for every irreducible representation
$\mathcal {S}$
is a basis of neighbourhoods of the identity consisting of compact open subgroups of G, notice that for every irreducible representation
![]() $\pi $
of G, there exists a group
$\pi $
of G, there exists a group
![]() $U\in \mathcal {S}$
such that
$U\in \mathcal {S}$
such that
![]() $\pi $
admits a nonzero U-invariant vector. In particular, for every irreducible representation
$\pi $
admits a nonzero U-invariant vector. In particular, for every irreducible representation
![]() $\pi $
of G, there exists a smallest nonnegative integer
$\pi $
of G, there exists a smallest nonnegative integer
![]() $l_\pi \in \mathbb N$
such that
$l_\pi \in \mathbb N$
such that
![]() $\pi $
admits nonzero U-invariant vectors for some
$\pi $
admits nonzero U-invariant vectors for some
![]() $U\in \mathcal {S}\lbrack l_\pi \rbrack $
. This
$U\in \mathcal {S}\lbrack l_\pi \rbrack $
. This
![]() $l_\pi $
is called the depth of
$l_\pi $
is called the depth of
![]() $\pi $
with respect to
$\pi $
with respect to
![]() $\mathcal {S}$
. The key notion developed in [Reference SemalSem23] is the notion of factorisation at depth l for a generic filtration
$\mathcal {S}$
. The key notion developed in [Reference SemalSem23] is the notion of factorisation at depth l for a generic filtration
![]() $\mathcal {S}$
, which we now recall.
$\mathcal {S}$
, which we now recall.
Definition 4.3. Let G be a nondiscrete unimodular totally disconnected locally compact group, let
![]() $\mathcal {S}$
be a generic filtration of G and let l be a strictly positive integer. We say that
$\mathcal {S}$
be a generic filtration of G and let l be a strictly positive integer. We say that
![]() $\mathcal {S}$
factorises at depth l if the following conditions hold.
$\mathcal {S}$
factorises at depth l if the following conditions hold.
-
(1) For all
 $U\in \mathcal {S}\lbrack l \rbrack $
and every V in the conjugacy class of an element of
$U\in \mathcal {S}\lbrack l \rbrack $
and every V in the conjugacy class of an element of
 $\mathcal {S}$
such that
$\mathcal {S}$
such that
 $V \not \subseteq U$
, there exists W in the conjugacy class of an element of
$V \not \subseteq U$
, there exists W in the conjugacy class of an element of
 $\mathcal {S}\lbrack l -1\rbrack $
such that
$\mathcal {S}\lbrack l -1\rbrack $
such that  $$ \begin{align*}U\subseteq W \subseteq V U=\{vu\mid u\in U, v\in V\}.\end{align*} $$
$$ \begin{align*}U\subseteq W \subseteq V U=\{vu\mid u\in U, v\in V\}.\end{align*} $$
-
(2) For all
 $U\in \mathcal {S}\lbrack l \rbrack $
and every V in the conjugacy class of an element of
$U\in \mathcal {S}\lbrack l \rbrack $
and every V in the conjugacy class of an element of
 $\mathcal {S}$
, the set is compact.
$\mathcal {S}$
, the set is compact. $$ \begin{align*} N_G(U, V)= \{g\in G \mid g^{-1}Vg\subseteq U\} \end{align*} $$
$$ \begin{align*} N_G(U, V)= \{g\in G \mid g^{-1}Vg\subseteq U\} \end{align*} $$
Furthermore, the generic filtration
![]() $\mathcal {S}$
of G is said to factorise
$\mathcal {S}$
of G is said to factorise
![]() $^+$
at depth l if in addition for all
$^+$
at depth l if in addition for all
![]() $U\in \mathcal {S}\lbrack l\rbrack $
and every W in the conjugacy class of an element of
$U\in \mathcal {S}\lbrack l\rbrack $
and every W in the conjugacy class of an element of
![]() $\mathcal {S}\lbrack l-1\rbrack $
such that
$\mathcal {S}\lbrack l-1\rbrack $
such that
![]() $U\subseteq W$
,
$U\subseteq W$
,
Since G is unimodular, notice that the set
![]() $N_G(U,U)$
coincides with the normaliser
$N_G(U,U)$
coincides with the normaliser
![]() $N_G(U)$
of U in G.
$N_G(U)$
of U in G.
The relevance of this notion is given by [Reference SemalSem23, Theorem A], which leads to a description of the irreducible representations at height l in terms of a family of irreducible representations of finite groups called
![]() $\mathcal {S}$
-standard representations (Definition 4.11 below), if the generic filtration factorises
$\mathcal {S}$
-standard representations (Definition 4.11 below), if the generic filtration factorises
![]() $^+$
at depth l.
$^+$
at depth l.
4.2 Generic filtration for
 $G^+_{(i)}(Y_0,Y_1)$
$G^+_{(i)}(Y_0,Y_1)$
Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 4$
and let
$d_0,d_1\geq 4$
and let
![]() $V(T)=V_0\sqcup V_1$
be the associated bipartition. Let i be a legal colouring of T and let
$V(T)=V_0\sqcup V_1$
be the associated bipartition. Let i be a legal colouring of T and let
![]() $Y_0,Y_1\subseteq \mathbb N$
be two finite subsets. The purpose of this section is to provide a generic filtration for
$Y_0,Y_1\subseteq \mathbb N$
be two finite subsets. The purpose of this section is to provide a generic filtration for
![]() $G_{(i)}^+(Y_0,Y_1)$
. To do this, let
$G_{(i)}^+(Y_0,Y_1)$
. To do this, let
![]() $\mathfrak {T}_0$
be the family of subtrees of T defined by
$\mathfrak {T}_0$
be the family of subtrees of T defined by
and consider the basis of neighbourhoods of the identity given by the fixators of these trees
Definition 4.4. A group
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
is said to satisfy the hypothesis
H
0
if for all
$G\leq \operatorname {\mathrm {Aut}}(T)$
is said to satisfy the hypothesis
H
0
if for all
![]() $\mathcal {T},\mathcal {T'}\in \mathfrak {T}_{0}$
,
$\mathcal {T},\mathcal {T'}\in \mathfrak {T}_{0}$
,
Lemma 4.5 [Reference SemalSem23, Lemma 4.12].
Let
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
be a closed nondiscrete unimodular subgroup satisfying the hypothesis H0
. Then,
$G\leq \operatorname {\mathrm {Aut}}(T)$
be a closed nondiscrete unimodular subgroup satisfying the hypothesis H0
. Then,
![]() $\mathcal {S}_{0}$
is a generic filtration of G and the sets
$\mathcal {S}_{0}$
is a generic filtration of G and the sets
![]() $\mathcal {S}_{0}\lbrack l \rbrack $
can be described as follows:
$\mathcal {S}_{0}\lbrack l \rbrack $
can be described as follows:
-
• if l is even,
 $\mathcal {S}_{0}\lbrack l\rbrack = \{\mathrm {Fix}_G(B_T(e,\tfrac {l}{2}))\mid e\in E(T)\};$
$\mathcal {S}_{0}\lbrack l\rbrack = \{\mathrm {Fix}_G(B_T(e,\tfrac {l}{2}))\mid e\in E(T)\};$
-
• if l is odd,
 $\mathcal {S}_{0}\lbrack l \rbrack =\{ \mathrm {Fix}_G(B_T(v,(({l+1})/{2})))\mid v\in V(T)\}.$
$\mathcal {S}_{0}\lbrack l \rbrack =\{ \mathrm {Fix}_G(B_T(v,(({l+1})/{2})))\mid v\in V(T)\}.$
We come back to our case
![]() $G=G^+_{(i)}(Y_0,Y_1)$
.
$G=G^+_{(i)}(Y_0,Y_1)$
.
Lemma 4.6. Let
![]() $G = G^+_{(i)}(Y_0,Y_1)$
and
$G = G^+_{(i)}(Y_0,Y_1)$
and
![]() $\mathcal {T}$
be a complete finite subtree of T. Then,
$\mathcal {T}$
be a complete finite subtree of T. Then,
![]() $\mathrm {Fix}_G(\mathcal {T})$
does not fix any vertices outside of
$\mathrm {Fix}_G(\mathcal {T})$
does not fix any vertices outside of
![]() $\mathcal {T}$
. In particular,
$\mathcal {T}$
. In particular,
![]() $G^+_{(i)}(Y_0,Y_1)$
satisfies the hypothesis (H0).
$G^+_{(i)}(Y_0,Y_1)$
satisfies the hypothesis (H0).
Proof. Since
![]() $H = G^+_{(i)}(\{0\},\{0\})$
is a subgroup of
$H = G^+_{(i)}(\{0\},\{0\})$
is a subgroup of
![]() $G^+_{(i)}(Y_0,Y_1)$
, it suffices to prove that
$G^+_{(i)}(Y_0,Y_1)$
, it suffices to prove that
![]() $\mathrm {Fix}_G(\mathcal {T})$
does not fix any vertices outside of
$\mathrm {Fix}_G(\mathcal {T})$
does not fix any vertices outside of
![]() $\mathcal {T}$
. If
$\mathcal {T}$
. If
![]() $\mathcal {T}$
has a single vertex, the result is trivial. Now, suppose that
$\mathcal {T}$
has a single vertex, the result is trivial. Now, suppose that
![]() $\mathcal {T}$
contains at least one edge. For each leaf w of
$\mathcal {T}$
contains at least one edge. For each leaf w of
![]() $\mathcal {T}$
, consider the unique vertex v of T that is adjacent to w and let
$\mathcal {T}$
, consider the unique vertex v of T that is adjacent to w and let
By choice of w, one has that
![]() $\mathcal {T}\subseteq T(v,w)\cup \{w\}$
and since H satisfies Tits’ independence property,
$\mathcal {T}\subseteq T(v,w)\cup \{w\}$
and since H satisfies Tits’ independence property,
![]() $\mathrm {Fix}_H(T(v,w))$
has a local action
$\mathrm {Fix}_H(T(v,w))$
has a local action
![]() $\operatorname {\mathrm {Alt}}(d-1)$
at w, where w has degree d. In particular, since
$\operatorname {\mathrm {Alt}}(d-1)$
at w, where w has degree d. In particular, since
![]() $d\geq 4$
,
$d\geq 4$
,
![]() $\mathrm {Fix}_H(\mathcal {T})\subseteq \mathrm {Fix}_H(T(v,w)\cup \{w\})=\mathrm {Fix}_H(T(v,w))$
does not fix any neighbour of w other than v and thus does not fix any vertices outside of
$\mathrm {Fix}_H(\mathcal {T})\subseteq \mathrm {Fix}_H(T(v,w)\cup \{w\})=\mathrm {Fix}_H(T(v,w))$
does not fix any neighbour of w other than v and thus does not fix any vertices outside of
![]() $T(v,w)\cup \{w\}$
. Since any vertex of T that does not belong to
$T(v,w)\cup \{w\}$
. Since any vertex of T that does not belong to
![]() $\mathcal {T}$
must be outside of one of these
$\mathcal {T}$
must be outside of one of these
![]() $T(v,w)\cup \{w\}$
, it follows that
$T(v,w)\cup \{w\}$
, it follows that
![]() $\mathrm {Fix}_H(\mathcal {T})$
does not fix any vertices outside of
$\mathrm {Fix}_H(\mathcal {T})$
does not fix any vertices outside of
![]() $\mathcal {T}$
and the result follows.
$\mathcal {T}$
and the result follows.
In particular, Lemma 4.5 ensures that
![]() $\mathcal {S}_0$
is a generic filtration of
$\mathcal {S}_0$
is a generic filtration of
![]() $G^+_{(i)}(Y_0,Y_1)$
.
$G^+_{(i)}(Y_0,Y_1)$
.
4.3 Factorisation
Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 4$
and let
$d_0,d_1\geq 4$
and let
![]() $V(T)=V_0\sqcup V_1$
be the associated bipartition. Let i be a legal colouring of T and let
$V(T)=V_0\sqcup V_1$
be the associated bipartition. Let i be a legal colouring of T and let
![]() $Y_0,Y_1\subseteq \mathbb N$
be two finite subsets. We have shown in Section 4.2 that
$Y_0,Y_1\subseteq \mathbb N$
be two finite subsets. We have shown in Section 4.2 that
![]() $\mathcal {S}_0$
is a generic filtration of
$\mathcal {S}_0$
is a generic filtration of
![]() $G_{(i)}^+(Y_0,Y_1)$
. The purpose of the present section is to prove that this generic filtration factorises
$G_{(i)}^+(Y_0,Y_1)$
. The purpose of the present section is to prove that this generic filtration factorises
![]() $^+$
at all depths
$^+$
at all depths
![]() $l\geq 1$
.
$l\geq 1$
.
We start with some notation that is used in the proof (see Figure 1). For any two distinct vertices
![]() $v,w\in V(T)$
, let
$v,w\in V(T)$
, let
![]() $\lbrack v,w\rbrack $
be the unique geodesic between v and w. Suppose that
$\lbrack v,w\rbrack $
be the unique geodesic between v and w. Suppose that
![]() $d(v,w)=n$
, let
$d(v,w)=n$
, let
![]() $v=v_0,v_1,\ldots ,v_n=w$
be the sequence of vertices corresponding to
$v=v_0,v_1,\ldots ,v_n=w$
be the sequence of vertices corresponding to
![]() $\lbrack v,w\rbrack $
in T, let
$\lbrack v,w\rbrack $
in T, let
and let
 $$ \begin{align*} T(v,w)&= \{x\in V(T)\mid d_T(x,p_{\lbrack v,w\rbrack }(w))<d_T(x,w)\}\\ &= \{x\in V(T)\mid d_T(x,v_{n-1})<d_T(x,w)\}. \end{align*} $$
$$ \begin{align*} T(v,w)&= \{x\in V(T)\mid d_T(x,p_{\lbrack v,w\rbrack }(w))<d_T(x,w)\}\\ &= \{x\in V(T)\mid d_T(x,v_{n-1})<d_T(x,w)\}. \end{align*} $$

Figure 1 The set
![]() $T(v,w)$
. Colour available online.
$T(v,w)$
. Colour available online.
The following intermediate result is the key ingredient needed to prove the factorisation of the generic filtration
![]() $\mathcal {S}_0$
of
$\mathcal {S}_0$
of
![]() $G_{(i)}^+(Y_0,Y_1)$
at all depths
$G_{(i)}^+(Y_0,Y_1)$
at all depths
![]() $l\geq 1$
.
$l\geq 1$
.
Proposition 4.7. For all
![]() $l,l'\in \mathbb N$
such that
$l,l'\in \mathbb N$
such that
![]() $l\geq 1$
and
$l\geq 1$
and
![]() $l'\geq l$
, for all U in the conjugacy class of an element of
$l'\geq l$
, for all U in the conjugacy class of an element of
![]() $\mathcal {S}_0\lbrack l \rbrack $
and every V in the conjugacy class of an element of
$\mathcal {S}_0\lbrack l \rbrack $
and every V in the conjugacy class of an element of
![]() $\mathcal {S}_0\lbrack l'\rbrack $
such that
$\mathcal {S}_0\lbrack l'\rbrack $
such that
![]() $V\not \subseteq U$
, there exists a subgroup
$V\not \subseteq U$
, there exists a subgroup
![]() $W\in \mathcal {S}_0\lbrack l-1\rbrack $
such that
$W\in \mathcal {S}_0\lbrack l-1\rbrack $
such that
![]() $U\subseteq W\subseteq VU$
.
$U\subseteq W\subseteq VU$
.
Proof. To shorten the proof and to make the argument clearer, parts of the reasoning are proved in Lemmas 4.8 and 4.9 below. Since the proof is quite long and technical, we first give an idea of its structure. We begin the proof by identifying the group W from U and V. We then prove that every element of W decomposes as a product of an element of V and an element of U. The proof of this decomposition is the technical part. It is achieved by a compactness argument taking advantage from the fact that
![]() $G_{(i)}^+(Y_0,Y_1)$
is defined by local action conditions.
$G_{(i)}^+(Y_0,Y_1)$
is defined by local action conditions.
Let
![]() $G= G_{(i)}^+(Y_0,Y_1)$
. As announced at the beginning of the proof, we start by identifying W. Notice that
$G= G_{(i)}^+(Y_0,Y_1)$
. As announced at the beginning of the proof, we start by identifying W. Notice that
![]() $\mathfrak {T}_0$
is stable under the action of G. Furthermore, for every
$\mathfrak {T}_0$
is stable under the action of G. Furthermore, for every
![]() $g\in \operatorname {\mathrm {Aut}}(T)^+$
and for every subtree
$g\in \operatorname {\mathrm {Aut}}(T)^+$
and for every subtree
![]() $\mathcal {T}$
of T, we have that
$\mathcal {T}$
of T, we have that
![]() $g\mathrm {Fix}_G(\mathcal {T})g^{-1}=\mathrm {Fix}_G(g\mathcal {T})$
. In particular, there exist
$g\mathrm {Fix}_G(\mathcal {T})g^{-1}=\mathrm {Fix}_G(g\mathcal {T})$
. In particular, there exist
![]() $\mathcal {T}$
,
$\mathcal {T}$
,
![]() $\mathcal {T}'\in \mathfrak {T}_0$
such that
$\mathcal {T}'\in \mathfrak {T}_0$
such that
![]() $U=\mathrm { Fix}_G(\mathcal {T})$
and
$U=\mathrm { Fix}_G(\mathcal {T})$
and
![]() $V=\mathrm {Fix}_G(\mathcal {T}')$
. Since
$V=\mathrm {Fix}_G(\mathcal {T}')$
. Since
![]() $V\not \subseteq U$
, notice that
$V\not \subseteq U$
, notice that
![]() $\mathcal {T}\not \subseteq \mathcal {T'}$
. If l is even, Lemma 4.5 ensures that
$\mathcal {T}\not \subseteq \mathcal {T'}$
. If l is even, Lemma 4.5 ensures that
![]() $\mathcal {T}=B_T(e,\tfrac {l}{2})$
for some edge
$\mathcal {T}=B_T(e,\tfrac {l}{2})$
for some edge
![]() $e\in E(T)$
. Furthermore, since
$e\in E(T)$
. Furthermore, since
![]() $\mathcal {T}\not \subseteq \mathcal {T'}$
and since
$\mathcal {T}\not \subseteq \mathcal {T'}$
and since
![]() $l'\geq l$
, there exists a unique vertex
$l'\geq l$
, there exists a unique vertex
![]() $v\in e$
such that
$v\in e$
such that
![]() $\mathcal {T}'\subseteq T(v,w)\cup B_T(v,\tfrac {l}{2})$
, where w denotes the other vertex of e. In this case, we let
$\mathcal {T}'\subseteq T(v,w)\cup B_T(v,\tfrac {l}{2})$
, where w denotes the other vertex of e. In this case, we let
![]() $\mathcal {T}_W=B_T(v,\tfrac {l}{2})$
. However, if l is odd, Lemma 4.5 ensures that
$\mathcal {T}_W=B_T(v,\tfrac {l}{2})$
. However, if l is odd, Lemma 4.5 ensures that
![]() $\mathcal {T}=B_T(w,({l+1})/{2})$
for some vertex
$\mathcal {T}=B_T(w,({l+1})/{2})$
for some vertex
![]() $w\in V(T)$
. Furthermore, since
$w\in V(T)$
. Furthermore, since
![]() $\mathcal {T}\not \subseteq \mathcal {T'}$
and since
$\mathcal {T}\not \subseteq \mathcal {T'}$
and since
![]() $l'\geq l$
, there exists a unique vertex
$l'\geq l$
, there exists a unique vertex
![]() $v\in B_T(w,1)-\{w\}$
such that
$v\in B_T(w,1)-\{w\}$
such that
![]() $\mathcal {T}'\subseteq T(v,w)\cup B_T(\{v,w\},({l-1})/{2})$
. In that case, we let
$\mathcal {T}'\subseteq T(v,w)\cup B_T(\{v,w\},({l-1})/{2})$
. In that case, we let
![]() $\mathcal {T}_W=B_T(\{v,w\},({l-1})/{2})$
. In both cases, we set
$\mathcal {T}_W=B_T(\{v,w\},({l-1})/{2})$
. In both cases, we set
![]() $W=\mathrm {Fix}_G( \mathcal {T}_W)$
. Notice by construction that
$W=\mathrm {Fix}_G( \mathcal {T}_W)$
. Notice by construction that
![]() $W\in \mathcal {S}_0\lbrack l-1\rbrack $
and that
$W\in \mathcal {S}_0\lbrack l-1\rbrack $
and that
![]() $U\subseteq W$
(since
$U\subseteq W$
(since
![]() $\mathcal {T}_W\subseteq \mathcal {T}$
). Our purpose is therefore to show that
$\mathcal {T}_W\subseteq \mathcal {T}$
). Our purpose is therefore to show that
![]() $W\subseteq V U$
. To this end, let
$W\subseteq V U$
. To this end, let
![]() $\alpha \in W$
and let us show the existence of an element
$\alpha \in W$
and let us show the existence of an element
![]() $\alpha _0\in U$
such that
$\alpha _0\in U$
such that ![]() . We start by explaining why the existence of
. We start by explaining why the existence of
![]() $\alpha _0$
settles the proof. Indeed, if
$\alpha _0$
settles the proof. Indeed, if
![]() $\alpha _0$
exists, notice that the automorphism
$\alpha _0$
exists, notice that the automorphism
![]() $\alpha _1=\alpha _0^{-1}\circ \alpha $
is an element of G for which
$\alpha _1=\alpha _0^{-1}\circ \alpha $
is an element of G for which ![]() . In particular, we have that
. In particular, we have that
![]() $\alpha _1\in \mathrm {Fix}_G(\mathcal {T}')$
,
$\alpha _1\in \mathrm {Fix}_G(\mathcal {T}')$
,
![]() $\alpha _0\in \mathrm {Fix}_G(\mathcal {T})$
and by construction
$\alpha _0\in \mathrm {Fix}_G(\mathcal {T})$
and by construction
![]() $\alpha =\alpha _0 \circ \alpha _1$
, which proves that
$\alpha =\alpha _0 \circ \alpha _1$
, which proves that
![]() $W\subseteq UV$
. Applying the inverse map on both sides of the inclusion, we obtain that
$W\subseteq UV$
. Applying the inverse map on both sides of the inclusion, we obtain that
![]() $W\subseteq VU$
which settles the proof.
$W\subseteq VU$
which settles the proof.
Now, let us prove the existence of
![]() $\alpha _0$
. As announced at the beginning of the proof, we are going to use a compactness argument taking advantage of the fact that
$\alpha _0$
. As announced at the beginning of the proof, we are going to use a compactness argument taking advantage of the fact that
![]() $G_{(i)}^+(Y_0,Y_1)$
is defined by local actions conditions. More precisely, we define a descending chain of nonempty compact sets
$G_{(i)}^+(Y_0,Y_1)$
is defined by local actions conditions. More precisely, we define a descending chain of nonempty compact sets
![]() $\Omega _n\subseteq \operatorname {\mathrm {Aut}}(T)^+$
and an increasing chain of finite subtrees
$\Omega _n\subseteq \operatorname {\mathrm {Aut}}(T)^+$
and an increasing chain of finite subtrees
![]() $\mathcal {R}_n$
of T such that
$\mathcal {R}_n$
of T such that
![]() $T=\bigcup _{n\in \mathbb N} \mathcal {R}_n$
and such that for all
$T=\bigcup _{n\in \mathbb N} \mathcal {R}_n$
and such that for all
![]() $h\in \Omega _n$
:
$h\in \Omega _n$
:
-
•
 $h\in \mathrm {Fix}_G(\mathcal {T})$
and
$h\in \mathrm {Fix}_G(\mathcal {T})$
and  ;
; -
•
 $\operatorname {\mathrm {Sgn}}_{(i)}(h,S_{Y_0}(v))=1$
for all v in
$\operatorname {\mathrm {Sgn}}_{(i)}(h,S_{Y_0}(v))=1$
for all v in
 $V_{t_0}\cap \mathcal {R}_n$
;
$V_{t_0}\cap \mathcal {R}_n$
; -
•
 $\operatorname {\mathrm {Sgn}}_{(i)}(h,S_{Y_1}(v))=1$
for all v in
$\operatorname {\mathrm {Sgn}}_{(i)}(h,S_{Y_1}(v))=1$
for all v in
 $V_{t_1}\cap \mathcal {R}_n$
.
$V_{t_1}\cap \mathcal {R}_n$
.
We recall that in the above,
![]() $t_0=\max (Y_0)\,\mod 2$
,
$t_0=\max (Y_0)\,\mod 2$
,
![]() $t_1=(1+\max (Y_1))\ \pmod{\,2}$
and
$t_1=(1+\max (Y_1))\ \pmod{\,2}$
and
![]() $\max (\varnothing )=0$
. Let us first show that this settles the existence of
$\max (\varnothing )=0$
. Let us first show that this settles the existence of
![]() $\alpha _0$
. Since the
$\alpha _0$
. Since the
![]() $\Omega _n$
form a descending chain of nonempty compact sets in a Hausdorff space, we obtain
$\Omega _n$
form a descending chain of nonempty compact sets in a Hausdorff space, we obtain
![]() $\bigcap _{n\in \mathbb N} \Omega _n\not =\varnothing $
. Let
$\bigcap _{n\in \mathbb N} \Omega _n\not =\varnothing $
. Let
![]() $\alpha _0 \in \bigcap _{n\in \mathbb N} \Omega _n$
. Since
$\alpha _0 \in \bigcap _{n\in \mathbb N} \Omega _n$
. Since
![]() $\alpha _0\in \Omega _0$
, notice that
$\alpha _0\in \Omega _0$
, notice that ![]() ,
, ![]() . To see that
. To see that
![]() $\alpha _0$
is as desired, all that remains is to show that
$\alpha _0$
is as desired, all that remains is to show that
![]() $\alpha _0\in G_{(i)}^+(Y_0,Y_1)$
. However, for every
$\alpha _0\in G_{(i)}^+(Y_0,Y_1)$
. However, for every
![]() $v\in V_{t}(T)$
, there exists a positive integer
$v\in V_{t}(T)$
, there exists a positive integer
![]() $n\in \mathbb N$
such that
$n\in \mathbb N$
such that
![]() $v\in \mathcal {R}_n$
and since
$v\in \mathcal {R}_n$
and since
![]() $\alpha _0\in \Omega _{n}$
, we have that
$\alpha _0\in \Omega _{n}$
, we have that
![]() $\operatorname {\mathrm {Sgn}}_{(i)}(\alpha _0,S_{Y_t}(v))=1$
. This proves that
$\operatorname {\mathrm {Sgn}}_{(i)}(\alpha _0,S_{Y_t}(v))=1$
. This proves that
![]() $\alpha _0$
is as desired.
$\alpha _0$
is as desired.

Figure 2 The tree
![]() $\mathcal {T}_W$
and the geodesic
$\mathcal {T}_W$
and the geodesic
![]() $\gamma $
. Colour available online.
$\gamma $
. Colour available online.
What remains is to define the descending chain of nonempty compact sets
![]() $\Omega _n\subseteq \operatorname {\mathrm {Aut}}(T)^+$
. Suppose that
$\Omega _n\subseteq \operatorname {\mathrm {Aut}}(T)^+$
. Suppose that
![]() $\max (Y_0)\leq \max (Y_1)$
(the proof for
$\max (Y_0)\leq \max (Y_1)$
(the proof for
![]() $\max (Y_1)\leq \max (Y_0)$
is similar). Let
$\max (Y_1)\leq \max (Y_0)$
is similar). Let
![]() $\gamma $
be the smallest geodesic of T that contains both the centre of
$\gamma $
be the smallest geodesic of T that contains both the centre of
![]() $\mathcal {T}$
and the centre of
$\mathcal {T}$
and the centre of
![]() $\mathcal {T}'$
, and is oriented from
$\mathcal {T}'$
, and is oriented from
![]() $\mathcal {T}$
to
$\mathcal {T}$
to
![]() $\mathcal {T}'$
(note that the centre is either a vertex or an edge depending on the values of l and
$\mathcal {T}'$
(note that the centre is either a vertex or an edge depending on the values of l and
![]() $l'$
). Since
$l'$
). Since
![]() $\mathcal {T}\not \subseteq \mathcal {T}'$
and since
$\mathcal {T}\not \subseteq \mathcal {T}'$
and since
![]() $l'\geq l$
, notice that
$l'\geq l$
, notice that
![]() $\gamma $
contains at least two vertices (see Figure 2). The increasing chain of finite subtrees
$\gamma $
contains at least two vertices (see Figure 2). The increasing chain of finite subtrees
![]() $\mathcal {R}_n$
of T such that
$\mathcal {R}_n$
of T such that
![]() $T=\bigcup _{n\in \mathbb N} \mathcal {R}_n$
that we are going to use is
$T=\bigcup _{n\in \mathbb N} \mathcal {R}_n$
that we are going to use is
![]() $\mathcal {R}_n=B_T(\gamma ,n)$
. We let
$\mathcal {R}_n=B_T(\gamma ,n)$
. We let
Since
![]() $\alpha \in \mathrm {Fix}_G(\mathcal {T}_W)$
and since
$\alpha \in \mathrm {Fix}_G(\mathcal {T}_W)$
and since
![]() $\mathcal {T}_W$
contains all vertices of
$\mathcal {T}_W$
contains all vertices of
![]() $\mathcal {T}\cap \mathcal {T}'$
, notice that
$\mathcal {T}\cap \mathcal {T}'$
, notice that
![]() $\Omega _{-1}$
is not empty. Now, since
$\Omega _{-1}$
is not empty. Now, since
![]() $\max (Y_0)\leq \max (Y_1)$
, notice that there exists a unique
$\max (Y_0)\leq \max (Y_1)$
, notice that there exists a unique
![]() $r\in \mathbb N$
such that
$r\in \mathbb N$
such that
![]() $\max (Y_0)+2r\leq \max (Y_1)\leq \max (Y_0)+2r +1$
(where one of these inequalities is an equality). We let
$\max (Y_0)+2r\leq \max (Y_1)\leq \max (Y_0)+2r +1$
(where one of these inequalities is an equality). We let
 $$ \begin{align*} \Omega_0=\left\{h\in \Omega_{-1}\ \middle\vert \begin{array}{@{\kern3pt}l@{}} \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_0}(v))=1 \mbox{ for each }v\in B_T(\gamma,2r)\cap V_{t_0}\\ \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_1}(v))=1 \mbox{ for each }v\in B_T(\gamma,0)\cap V_{t_1} \end{array}\right\}. \end{align*} $$
$$ \begin{align*} \Omega_0=\left\{h\in \Omega_{-1}\ \middle\vert \begin{array}{@{\kern3pt}l@{}} \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_0}(v))=1 \mbox{ for each }v\in B_T(\gamma,2r)\cap V_{t_0}\\ \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_1}(v))=1 \mbox{ for each }v\in B_T(\gamma,0)\cap V_{t_1} \end{array}\right\}. \end{align*} $$
Lemma 4.8 below ensures that this set is not empty. From there, we define the sets
![]() $\Omega _n$
by induction on n. For every
$\Omega _n$
by induction on n. For every
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $h_n$
be an element of
$h_n$
be an element of
![]() $\Omega _{n-1}$
and let
$\Omega _{n-1}$
and let

For this induction to make sense, it is important for
![]() $\Omega _{n}$
to be not empty for all
$\Omega _{n}$
to be not empty for all
![]() $n\geq 1$
. This is proved by Lemma 4.9 below, which ensures that
$n\geq 1$
. This is proved by Lemma 4.9 below, which ensures that
![]() $\Omega _{n}$
is a nonempty compact set. The result follows.
$\Omega _{n}$
is a nonempty compact set. The result follows.
Our current purpose is to prove Lemmas 4.8 and 4.9. To this end, we introduce some formalism that is used in both proofs. For all
![]() $v\in V(T)$
, we need an automorphism
$v\in V(T)$
, we need an automorphism
![]() $h_{(v)}\in \operatorname {\mathrm {Aut}}(T)^+$
that is used to create an element of
$h_{(v)}\in \operatorname {\mathrm {Aut}}(T)^+$
that is used to create an element of
![]() $\omega _{n+1}$
from an element of
$\omega _{n+1}$
from an element of
![]() $\Omega _n$
. We start by choosing four functions:
$\Omega _n$
. We start by choosing four functions:
such that
![]() $\phi _t(k)$
is an odd permutation of
$\phi _t(k)$
is an odd permutation of
![]() $\operatorname {\mathrm {Sym}}(d_t)$
that fixes k and
$\operatorname {\mathrm {Sym}}(d_t)$
that fixes k and
![]() $\tilde {\phi }_t(k,l)$
is an odd permutation of
$\tilde {\phi }_t(k,l)$
is an odd permutation of
![]() $\operatorname {\mathrm {Sym}}(d_t)$
that fixes k and l.
$\operatorname {\mathrm {Sym}}(d_t)$
that fixes k and l.
If
![]() $v\in V(T)-\gamma $
, we choose
$v\in V(T)-\gamma $
, we choose
![]() $w\in \gamma $
and let
$w\in \gamma $
and let
![]() $h_{(v)}\in \operatorname {\mathrm {Aut}}(T)^+$
be such that:
$h_{(v)}\in \operatorname {\mathrm {Aut}}(T)^+$
be such that:
-
(1)
 $h_{(v)}\in \mathrm {Fix}_{\operatorname {\mathrm {Aut}}(T)^+}(T(p_{\lbrack w,v\rbrack }(v),v))$
;
$h_{(v)}\in \mathrm {Fix}_{\operatorname {\mathrm {Aut}}(T)^+}(T(p_{\lbrack w,v\rbrack }(v),v))$
; -
(2)
 $\sigma _{(i)}(h_{(v)},v)=\phi _t(i(p_{[w,v]}(v)))$
, where
$\sigma _{(i)}(h_{(v)},v)=\phi _t(i(p_{[w,v]}(v)))$
, where
 $t\in \{0,1\}$
is such that
$t\in \{0,1\}$
is such that
 $v\in V_t$
.
$v\in V_t$
.
Notice that for all
![]() $v\in V(T)-\gamma $
and every
$v\in V(T)-\gamma $
and every
![]() $w,w'\in \gamma $
,
$w,w'\in \gamma $
,
![]() $p_{\lbrack w,v\rbrack }(v) = p_{\lbrack w',v\rbrack }(v)$
(recall the definition of
$p_{\lbrack w,v\rbrack }(v) = p_{\lbrack w',v\rbrack }(v)$
(recall the definition of
![]() $p_{\lbrack w,v\rbrack }$
from Section 4.3) so that our choice of
$p_{\lbrack w,v\rbrack }$
from Section 4.3) so that our choice of
![]() $w\in \gamma $
does not change the two properties that
$w\in \gamma $
does not change the two properties that
![]() $h_{(v)}$
must satisfy (see Figure 3).
$h_{(v)}$
must satisfy (see Figure 3).

Figure 3 The automorphism
![]() $h_{(v)}$
. Colour available online.
$h_{(v)}$
. Colour available online.
If
![]() $v\in \gamma $
, we have two cases. Remember that
$v\in \gamma $
, we have two cases. Remember that
![]() $\gamma $
has at least two vertices. If v is an end of
$\gamma $
has at least two vertices. If v is an end of
![]() $\gamma $
, let w be the unique vertex of
$\gamma $
, let w be the unique vertex of
![]() $\gamma $
that is adjacent to v and choose an automorphism
$\gamma $
that is adjacent to v and choose an automorphism
![]() $h_{(v)}\in \operatorname {\mathrm {Aut}}(T)^+$
such that:
$h_{(v)}\in \operatorname {\mathrm {Aut}}(T)^+$
such that:
-
(1)
 $h_{(v)}\in \mathrm {Fix}_{\operatorname {\mathrm {Aut}}(T)^+}(T(w,v))$
;
$h_{(v)}\in \mathrm {Fix}_{\operatorname {\mathrm {Aut}}(T)^+}(T(w,v))$
; -
(2)
 $\sigma _{(i)}(h_{(v)},v)=\phi _t(i(w))$
, where
$\sigma _{(i)}(h_{(v)},v)=\phi _t(i(w))$
, where
 $t\in \{0,1\}$
is such that
$t\in \{0,1\}$
is such that
 $v\in V_t$
.
$v\in V_t$
.
However, if v is not an end of
![]() $\gamma $
, let
$\gamma $
, let
![]() $w_1,w_2$
be the two neighbours of v that belong to
$w_1,w_2$
be the two neighbours of v that belong to
![]() $\gamma $
and choose an automorphism
$\gamma $
and choose an automorphism
![]() $h_{(v)}\in \operatorname {\mathrm {Aut}}(T)^+$
such that:
$h_{(v)}\in \operatorname {\mathrm {Aut}}(T)^+$
such that:
-
(1)
 $h_{(v)}\in \mathrm {Fix}_{\operatorname {\mathrm {Aut}}(T)^+}(T(w_1,v)\cup T(w_2,v))$
;
$h_{(v)}\in \mathrm {Fix}_{\operatorname {\mathrm {Aut}}(T)^+}(T(w_1,v)\cup T(w_2,v))$
; -
(2)
 $\sigma _{(i)}(h_{(v)},v)=\tilde {\phi }_t(i(w_1),i(w_2))$
, where
$\sigma _{(i)}(h_{(v)},v)=\tilde {\phi }_t(i(w_1),i(w_2))$
, where
 $t\in \{0,1\}$
is such that
$t\in \{0,1\}$
is such that
 $v\in V_t$
.
$v\in V_t$
.
We are now ready to prove Lemmas 4.8 and 4.9.
Lemma 4.8. The set
 $$ \begin{align*} \Omega_0=\left\{h\in \Omega_{-1}\ \middle\vert\ \begin{array}{@{}l@{}} \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_0}(v))=1 \mbox{ for each }v\in B_T(\gamma,2r)\cap V_{t_0}\\ \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_1}(v))=1 \mbox{ for each }v\in B_T(\gamma,0)\cap V_{t_1} \end{array}\right\}. \end{align*} $$
$$ \begin{align*} \Omega_0=\left\{h\in \Omega_{-1}\ \middle\vert\ \begin{array}{@{}l@{}} \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_0}(v))=1 \mbox{ for each }v\in B_T(\gamma,2r)\cap V_{t_0}\\ \operatorname{\mathrm{Sgn}}_{(i)}(g,S_{Y_1}(v))=1 \mbox{ for each }v\in B_T(\gamma,0)\cap V_{t_1} \end{array}\right\}. \end{align*} $$
is not empty.
Proof. We recall that
![]() $\max (Y_0)\leq \max (Y_1)$
, that
$\max (Y_0)\leq \max (Y_1)$
, that
![]() $r\in \mathbb N$
is the unique integer such that
$r\in \mathbb N$
is the unique integer such that
![]() $\max (Y_0)+2r\leq \max (Y_1)\leq \max (Y_0)+2r +1$
, that
$\max (Y_0)+2r\leq \max (Y_1)\leq \max (Y_0)+2r +1$
, that
![]() ${t_0=\max (Y_0) \ \pmod{\,2}}$
and that
${t_0=\max (Y_0) \ \pmod{\,2}}$
and that
![]() ${t_1=(\max (Y_1)+1) \ \pmod{\,2}}$
. Remember from the proof of Proposition 4.7 that
${t_1=(\max (Y_1)+1) \ \pmod{\,2}}$
. Remember from the proof of Proposition 4.7 that
![]() $\Omega _{-1}$
is not empty and let
$\Omega _{-1}$
is not empty and let
![]() $h_0\in \Omega _{-1}$
. We are going to modify the element
$h_0\in \Omega _{-1}$
. We are going to modify the element
![]() $h_0$
with the automorphisms
$h_0$
with the automorphisms
![]() $h_{(v)}$
to get an element of
$h_{(v)}$
to get an element of
![]() $\Omega _{0}$
. A concrete example of the procedure is given on a
$\Omega _{0}$
. A concrete example of the procedure is given on a
![]() $4$
-regular tree with
$4$
-regular tree with
![]() $Y_0=\{0\}$
and
$Y_0=\{0\}$
and
![]() $Y_1=\{1,2\}$
by Figures 4, 5 and 6. In these figures:
$Y_1=\{1,2\}$
by Figures 4, 5 and 6. In these figures:
-
• the hollow vertices are those considered by the current and previous steps;
-
• the circled vertices are those for which we wish to change the sign
 $\operatorname {\mathrm {Sgn}}_{(i)}(g,S_{Y_0}(v))$
or
$\operatorname {\mathrm {Sgn}}_{(i)}(g,S_{Y_0}(v))$
or
 $\operatorname {\mathrm {Sgn}}_{(i)}(g,S_{Y_1}(v))$
(depending on the step) without affecting the sign of other hollow vertices;
$\operatorname {\mathrm {Sgn}}_{(i)}(g,S_{Y_1}(v))$
(depending on the step) without affecting the sign of other hollow vertices; -
• the vertices boxed in squares are the vertices for which a change of the local action is applied to achieve the desired change of sign (note that for our choice
 $Y_0=\{0\}$
, these vertices are also the circled vertices).
$Y_0=\{0\}$
, these vertices are also the circled vertices).

Figure 4 Step I of the proof of Lemma 4.8. Colour available online.

Figure 5 Step II of the proof of Lemma 4.8. Colour available online.

Figure 6 Step III of the proof of Lemma 4.8. Colour available online.
Let
![]() $\{w_{0,0},\ldots ,w_{0,m_0}\}$
be the set of vertices
$\{w_{0,0},\ldots ,w_{0,m_0}\}$
be the set of vertices
![]() $w\in B_T(\gamma ,0)\cap V_{t_0}$
such that
$w\in B_T(\gamma ,0)\cap V_{t_0}$
such that
![]() ${\operatorname {\mathrm {Sgn}}_{(i)}(h_0,S_{Y_0}(w))=-1}$
. For all
${\operatorname {\mathrm {Sgn}}_{(i)}(h_0,S_{Y_0}(w))=-1}$
. For all
![]() $j=0,1,\ldots ,m_0$
, we choose a vertex
$j=0,1,\ldots ,m_0$
, we choose a vertex
 $$ \begin{align*}v_{0,j}\in \bigcap_{w\in \gamma-\{w_{0,j}\}}{}T(w_{0,j},w)\end{align*} $$
$$ \begin{align*}v_{0,j}\in \bigcap_{w\in \gamma-\{w_{0,j}\}}{}T(w_{0,j},w)\end{align*} $$
such that
![]() $d(v_{0,j},w_{0,j})=\max (Y_0)$
. In particular, notice that
$d(v_{0,j},w_{0,j})=\max (Y_0)$
. In particular, notice that
![]() $v_{0,j}\in S_{Y_0}(w_{0,j})$
but that
$v_{0,j}\in S_{Y_0}(w_{0,j})$
but that
![]() ${v_{0,j}\not \in S_{Y_0}(w)}$
for every
${v_{0,j}\not \in S_{Y_0}(w)}$
for every
![]() $w \in B_T(\gamma ,0)\cap V_{t_0}-\{w_{0,j}\} $
. Furthermore, since
$w \in B_T(\gamma ,0)\cap V_{t_0}-\{w_{0,j}\} $
. Furthermore, since
![]() $\operatorname {\mathrm {Sgn}}_{(i)}(h_0,S_{Y_0}(w_{0,j}))=-1$
,
$\operatorname {\mathrm {Sgn}}_{(i)}(h_0,S_{Y_0}(w_{0,j}))=-1$
, ![]() ,
, ![]() , and due to the form of
, and due to the form of
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}'$
, the vertices
$\mathcal {T}'$
, the vertices
![]() $v_{0,j}$
must be such that the automorphisms
$v_{0,j}$
must be such that the automorphisms
![]() $h_{(v_{0,0})},\ldots , h_{(v_{0,m_0})}$
fix
$h_{(v_{0,0})},\ldots , h_{(v_{0,m_0})}$
fix
![]() $\mathcal {T}\cup \mathcal {T}'$
pointwise. Indeed, if
$\mathcal {T}\cup \mathcal {T}'$
pointwise. Indeed, if
![]() $v_{0,j}$
is outside the trees
$v_{0,j}$
is outside the trees
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}'$
or is a leaf of either of these trees, the conclusion is clear. Furthermore,
$\mathcal {T}'$
or is a leaf of either of these trees, the conclusion is clear. Furthermore,
![]() $v_{0,j}$
can not be an interior vertex of
$v_{0,j}$
can not be an interior vertex of
![]() $\mathcal {T}$
or
$\mathcal {T}$
or
![]() $\mathcal {T}'$
, since
$\mathcal {T}'$
, since
![]() $\operatorname {\mathrm {Sgn}}_{(i)}(h_0,S_{Y_0}(w_{0,j})) = -1$
and
$\operatorname {\mathrm {Sgn}}_{(i)}(h_0,S_{Y_0}(w_{0,j})) = -1$
and
![]() $h_0\in \Omega _{-1}$
. In particular, if
$h_0\in \Omega _{-1}$
. In particular, if
![]() $v_{0,j}$
was an interior vertex of
$v_{0,j}$
was an interior vertex of
![]() $\mathcal {T}$
,
$\mathcal {T}$
,
![]() $w_{0,j}$
would be too far inside
$w_{0,j}$
would be too far inside
![]() $\mathcal {T}$
to have
$\mathcal {T}$
to have
![]() $\operatorname {\mathrm {Sgn}}_{(i)}(h_0,S_{Y_0}(w_{0,j})) = -1$
as
$\operatorname {\mathrm {Sgn}}_{(i)}(h_0,S_{Y_0}(w_{0,j})) = -1$
as
![]() $h_0$
fixes pointwise a large enough ball around
$h_0$
fixes pointwise a large enough ball around
![]() $w_{0,j}$
and if
$w_{0,j}$
and if
![]() $v_{0,j}$
was an interior vertex of
$v_{0,j}$
was an interior vertex of
![]() $\mathcal {T}'$
,
$\mathcal {T}'$
,
![]() $w_{0,j}$
would be too far inside
$w_{0,j}$
would be too far inside
![]() $\mathcal {T}'$
to have
$\mathcal {T}'$
to have
![]() $\operatorname {\mathrm {Sgn}}_{(i)}(h_0,S_{Y_0}(w_{0,j})) = -1$
as
$\operatorname {\mathrm {Sgn}}_{(i)}(h_0,S_{Y_0}(w_{0,j})) = -1$
as
![]() $h_0$
agrees with
$h_0$
agrees with
![]() $\alpha $
on a large enough ball around
$\alpha $
on a large enough ball around
![]() $w_{0,j}$
. This proves as desired that the automorphisms
$w_{0,j}$
. This proves as desired that the automorphisms
![]() $h_{(v_{0,0})},\ldots , h_{(v_{0,m_0})}$
fix
$h_{(v_{0,0})},\ldots , h_{(v_{0,m_0})}$
fix
![]() $\mathcal {T}\cup \mathcal {T}'$
pointwise. In particular, the automorphism
$\mathcal {T}\cup \mathcal {T}'$
pointwise. In particular, the automorphism
satisfies ![]() ,
, ![]() and
and
If
![]() $r\not =0$
, we iterate this procedure. For every
$r\not =0$
, we iterate this procedure. For every
![]() $1\leq \nu \leq 2r$
, let
$1\leq \nu \leq 2r$
, let
![]() $\{w_{\nu ,0},\ldots ,w_{\nu ,m_{\nu }}\}$
be the set of vertices
$\{w_{\nu ,0},\ldots ,w_{\nu ,m_{\nu }}\}$
be the set of vertices
![]() $w\in B_T(\gamma ,\nu )\cap V_{t_0}$
such that
$w\in B_T(\gamma ,\nu )\cap V_{t_0}$
such that
For all
![]() $j=0,1,\ldots ,m_\nu $
, we choose a vertex
$j=0,1,\ldots ,m_\nu $
, we choose a vertex
 $$ \begin{align*}v_{\nu,j}\in \bigcap_{w\in B_T(\gamma,\nu)\cap V_{t_0}-\{w_{\nu,j}\}}{}T(w_{\nu,j},w)\end{align*} $$
$$ \begin{align*}v_{\nu,j}\in \bigcap_{w\in B_T(\gamma,\nu)\cap V_{t_0}-\{w_{\nu,j}\}}{}T(w_{\nu,j},w)\end{align*} $$
such that
![]() $d(v_{\nu ,j},w_{\nu ,j})=\max (Y_0)$
. Hence, notice that
$d(v_{\nu ,j},w_{\nu ,j})=\max (Y_0)$
. Hence, notice that
![]() $v_{\nu ,j}\in S_{Y_0}(w_{\nu ,j})$
but that
$v_{\nu ,j}\in S_{Y_0}(w_{\nu ,j})$
but that
![]() $v_{\nu ,j}\not \in S_{Y_0}(w)$
for every
$v_{\nu ,j}\not \in S_{Y_0}(w)$
for every
![]() $w\in B_T(\gamma ,\nu )\cap V_{t_0}-\{w_{\nu ,j}\}$
. Furthermore, notice that the automorphisms
$w\in B_T(\gamma ,\nu )\cap V_{t_0}-\{w_{\nu ,j}\}$
. Furthermore, notice that the automorphisms
![]() $h_{(v_{\nu ,0})}, \ldots , h_{(v_{\nu ,m_\nu })}$
fix
$h_{(v_{\nu ,0})}, \ldots , h_{(v_{\nu ,m_\nu })}$
fix
![]() $\mathcal {T}\cup \mathcal {T}'$
pointwise. In particular, the automorphism
$\mathcal {T}\cup \mathcal {T}'$
pointwise. In particular, the automorphism
satisfies that ![]() ,
, ![]() and
and
Consider the element
![]() $h_{2r,0}$
that we have just constructed. This element behaves as desired for the condition given by
$h_{2r,0}$
that we have just constructed. This element behaves as desired for the condition given by
![]() $Y_0$
on the vertices of
$Y_0$
on the vertices of
![]() $B_T(\gamma ,2r)\cap V_{t_0}$
. However, nothing ensures that the condition given by
$B_T(\gamma ,2r)\cap V_{t_0}$
. However, nothing ensures that the condition given by
![]() $Y_1$
on the vertices of
$Y_1$
on the vertices of
![]() $B_T(\gamma ,0)\cap V_{t_1}$
is yet satisfied. We now take care of this task. Let
$B_T(\gamma ,0)\cap V_{t_1}$
is yet satisfied. We now take care of this task. Let
![]() $\{w_0,\ldots ,w_m\}$
be the set of vertices
$\{w_0,\ldots ,w_m\}$
be the set of vertices
![]() $w\in B_T( \gamma ,0)\cap V_{t_1}$
such that
$w\in B_T( \gamma ,0)\cap V_{t_1}$
such that
![]() $\operatorname {\mathrm {Sgn}}_{(i)}(h_{2r,0},S_{Y_1}(w))=-1$
. For all
$\operatorname {\mathrm {Sgn}}_{(i)}(h_{2r,0},S_{Y_1}(w))=-1$
. For all
![]() $j=0,1,\ldots ,m$
, let
$j=0,1,\ldots ,m$
, let
![]() ${v_j\in \bigcap _{w\in \gamma -\{w_j\}} T(w_j,w)}$
such that
${v_j\in \bigcap _{w\in \gamma -\{w_j\}} T(w_j,w)}$
such that
![]() $d(v_j,w_j)=\max (Y_1)$
. In particular, notice that
$d(v_j,w_j)=\max (Y_1)$
. In particular, notice that
![]() $v_{j}\in S_{Y_1}(w_{j})$
but that
$v_{j}\in S_{Y_1}(w_{j})$
but that
![]() $v_{j}\not \in S_{Y_1}(w)$
for every
$v_{j}\not \in S_{Y_1}(w)$
for every
![]() $w\in B_T(\gamma ,0) \cap V_{t_1}-\{w_j\}$
. Furthermore, since
$w\in B_T(\gamma ,0) \cap V_{t_1}-\{w_j\}$
. Furthermore, since
![]() $\max (Y_0)+2r\leq \max (Y_1)$
, notice from Remark 3.4 that
$\max (Y_0)+2r\leq \max (Y_1)$
, notice from Remark 3.4 that
![]() $v_j\not \in S_{Y_0}(v)$
for every
$v_j\not \in S_{Y_0}(v)$
for every
![]() $v\in B_T(\gamma ,2r)\cap V_{t_0}$
. However, just as before, the automorphisms
$v\in B_T(\gamma ,2r)\cap V_{t_0}$
. However, just as before, the automorphisms
![]() $h_{(v_{0})}, \ldots , h_{(v_{m})}$
fix
$h_{(v_{0})}, \ldots , h_{(v_{m})}$
fix
![]() $\mathcal {T}\cup \mathcal {T}'$
pointwise. In particular,
$\mathcal {T}\cup \mathcal {T}'$
pointwise. In particular,
![]() $h_{1}= h_{2r,0}\circ h_{(v_{0})}\circ \cdots \circ h_{(v_{m})}$
satisfies:
$h_{1}= h_{2r,0}\circ h_{(v_{0})}\circ \cdots \circ h_{(v_{m})}$
satisfies:
-
•
 and
and  ;
; -
•
 $\operatorname {\mathrm {Sgn}}_{(i)}(h_{1},S_{Y_0}(w))=1 \text { for all } w\in B_T(\gamma ,2r)\cap V_{t_0};$
$\operatorname {\mathrm {Sgn}}_{(i)}(h_{1},S_{Y_0}(w))=1 \text { for all } w\in B_T(\gamma ,2r)\cap V_{t_0};$
-
•
 $\operatorname {\mathrm {Sgn}}_{(i)}(h_{1},S_{Y_1}(w))=1 \text { for all } w\in B_T(\gamma ,0)\cap V_{t_1}.$
$\operatorname {\mathrm {Sgn}}_{(i)}(h_{1},S_{Y_1}(w))=1 \text { for all } w\in B_T(\gamma ,0)\cap V_{t_1}.$
This proves that
![]() $h_1\in \Omega _0$
and therefore that
$h_1\in \Omega _0$
and therefore that
![]() $\Omega _0$
is not empty.
$\Omega _0$
is not empty.
Lemma 4.9. For all
![]() $n\geq 1$
, the set
$n\geq 1$
, the set

is a nonempty compact subset of
![]() $\operatorname {\mathrm {Aut}}(T)^+$
.
$\operatorname {\mathrm {Aut}}(T)^+$
.

Figure 7 Step I of the proof of Lemma 4.9. Colour available online.

Figure 8 Step II of the proof of Lemma 4.9. Colour available online.
Proof. We show that
![]() $\Omega _n$
is not empty by induction. Lemma 4.8 ensures that
$\Omega _n$
is not empty by induction. Lemma 4.8 ensures that
![]() $\Omega _0$
is not empty. Suppose that
$\Omega _0$
is not empty. Suppose that
![]() $\Omega _{n-1}$
is not empty and let
$\Omega _{n-1}$
is not empty and let
![]() $h_n\in \Omega _{n-1}$
be the automorphism appearing in the definition of
$h_n\in \Omega _{n-1}$
be the automorphism appearing in the definition of
![]() $\Omega _n$
. Just as in the proof of Lemma 4.8, we are going to modify
$\Omega _n$
. Just as in the proof of Lemma 4.8, we are going to modify
![]() $h_n$
with the automorphisms
$h_n$
with the automorphisms
![]() $h_{(v)}$
to obtain an element of
$h_{(v)}$
to obtain an element of
![]() $\Omega _{n}$
. A concrete example of the procedure is given by Figures 7 and 8 on a
$\Omega _{n}$
. A concrete example of the procedure is given by Figures 7 and 8 on a
![]() $4$
-regular tree with
$4$
-regular tree with
![]() $Y_0=\{0\}$
and even
$Y_0=\{0\}$
and even
![]() $\max {(Y_1)}$
(with the same conventions as before and where the vertices concerned by the current step are highlighted in dotted areas). Let
$\max {(Y_1)}$
(with the same conventions as before and where the vertices concerned by the current step are highlighted in dotted areas). Let
![]() $\{\tilde {w}_0,\ldots ,\tilde {w}_{k}\}$
be the set of vertices
$\{\tilde {w}_0,\ldots ,\tilde {w}_{k}\}$
be the set of vertices
![]() $w$
that belong to
$w$
that belong to
![]() $ B_T(\gamma ,n+2r)\cap V_{t_0}$
and such that
$ B_T(\gamma ,n+2r)\cap V_{t_0}$
and such that
![]() $\operatorname {\mathrm {Sgn}}_{(i)}(h_n,S_{Y_0}(w))=-1$
. For each
$\operatorname {\mathrm {Sgn}}_{(i)}(h_n,S_{Y_0}(w))=-1$
. For each
![]() $j=0,1,\ldots ,k$
, we choose a vertex
$j=0,1,\ldots ,k$
, we choose a vertex
![]() ${\tilde {v}_{j}\in \bigcap _{w\in B_T(\gamma ,n+2r)\cap V_{t_0}-\{\tilde {w}_j\}}{}T(\tilde {w}_{j},w)}$
such that
${\tilde {v}_{j}\in \bigcap _{w\in B_T(\gamma ,n+2r)\cap V_{t_0}-\{\tilde {w}_j\}}{}T(\tilde {w}_{j},w)}$
such that
![]() $d(\tilde {v}_{j},\tilde {w}_{j})=\max (Y_0)$
. Hence, notice that
$d(\tilde {v}_{j},\tilde {w}_{j})=\max (Y_0)$
. Hence, notice that
![]() $\tilde {v}_j\not \in S_{Y_0}(w)$
for all
$\tilde {v}_j\not \in S_{Y_0}(w)$
for all
![]() ${w\in B_T(\gamma ,n+2r)\cap V_{t_0}-\{\tilde {w}_j\}}$
. Furthermore, since
${w\in B_T(\gamma ,n+2r)\cap V_{t_0}-\{\tilde {w}_j\}}$
. Furthermore, since
![]() $\max (Y_1)-1\leq 2r+\max (Y_0)$
, notice from Remark 3.4 that
$\max (Y_1)-1\leq 2r+\max (Y_0)$
, notice from Remark 3.4 that
![]() $\tilde {v}_j\not \in S_{Y_1}(w)$
for all
$\tilde {v}_j\not \in S_{Y_1}(w)$
for all
![]() ${w\in B_T(\gamma ,n-1)\cap V_{t_1}}$
. Furthermore, since
${w\in B_T(\gamma ,n-1)\cap V_{t_1}}$
. Furthermore, since
![]() ${\operatorname {\mathrm {Sgn}}_{(i)}(h_{n},S_{Y_0}(\tilde {w}_{j}))=-1}$
,
${\operatorname {\mathrm {Sgn}}_{(i)}(h_{n},S_{Y_0}(\tilde {w}_{j}))=-1}$
, ![]() ,
, ![]() , and due to the form’s of
, and due to the form’s of
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}'$
, notice that the automorphisms
$\mathcal {T}'$
, notice that the automorphisms
![]() $h_{(\tilde {v}_{0})}, \ldots , h_{(\tilde {v}_{k})}$
fix
$h_{(\tilde {v}_{0})}, \ldots , h_{(\tilde {v}_{k})}$
fix
![]() $\mathcal {T}\cup \mathcal {T}'$
pointwise. Indeed, if
$\mathcal {T}\cup \mathcal {T}'$
pointwise. Indeed, if
![]() $\tilde {v}_{j}$
is outside the trees
$\tilde {v}_{j}$
is outside the trees
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}'$
or is a leaf of either of these trees, the conclusion is clear. However,
$\mathcal {T}'$
or is a leaf of either of these trees, the conclusion is clear. However,
![]() $\tilde {v}_{j}$
cannot be an interior vertex of
$\tilde {v}_{j}$
cannot be an interior vertex of
![]() $\mathcal {T}$
or
$\mathcal {T}$
or
![]() $\mathcal {T}'$
, since
$\mathcal {T}'$
, since
![]() $\operatorname {\mathrm {Sgn}}_{(i)}(h_n,S_{Y_0}(\tilde {w}_{j})) = -1$
and
$\operatorname {\mathrm {Sgn}}_{(i)}(h_n,S_{Y_0}(\tilde {w}_{j})) = -1$
and
![]() $h_n\in \Omega _{n-1}$
. In particular, if
$h_n\in \Omega _{n-1}$
. In particular, if
![]() $\tilde {v}_{j}$
was an interior vertex of
$\tilde {v}_{j}$
was an interior vertex of
![]() $\mathcal {T}$
,
$\mathcal {T}$
,
![]() $\tilde {w}_{j}$
would be too far inside
$\tilde {w}_{j}$
would be too far inside
![]() $\mathcal {T}$
for
$\mathcal {T}$
for
![]() $\operatorname {\mathrm {Sgn}}_{(i)}(h_n,S_{Y_0}(\tilde {w}_{j})) = -1$
as
$\operatorname {\mathrm {Sgn}}_{(i)}(h_n,S_{Y_0}(\tilde {w}_{j})) = -1$
as
![]() $h_n$
fixes pointwise a large enough ball around
$h_n$
fixes pointwise a large enough ball around
![]() $\tilde {w}_{j}$
and if
$\tilde {w}_{j}$
and if
![]() $\tilde {v}_{j}$
was an interior vertex of
$\tilde {v}_{j}$
was an interior vertex of
![]() $\mathcal {T}'$
,
$\mathcal {T}'$
,
![]() $\tilde {w}_{j}$
would be too far inside
$\tilde {w}_{j}$
would be too far inside
![]() $\mathcal {T}'$
for
$\mathcal {T}'$
for
![]() $\operatorname {\mathrm {Sgn}}_{(i)}(h_n,S_{Y_0}(\tilde {w}_{j})) = -1$
as
$\operatorname {\mathrm {Sgn}}_{(i)}(h_n,S_{Y_0}(\tilde {w}_{j})) = -1$
as
![]() $h_n$
agrees with
$h_n$
agrees with
![]() $\alpha $
on a large enough ball around
$\alpha $
on a large enough ball around
![]() $\tilde {w}_{j}$
. This proves as desired that the automorphisms
$\tilde {w}_{j}$
. This proves as desired that the automorphisms
![]() $h_{(\tilde {v}_{0})}, \ldots , h_{(\tilde {v}_{k})}$
fix
$h_{(\tilde {v}_{0})}, \ldots , h_{(\tilde {v}_{k})}$
fix
![]() $\mathcal {T}\cup \mathcal {T}'$
pointwise. In particular,
$\mathcal {T}\cup \mathcal {T}'$
pointwise. In particular,
![]() $\tilde {h}_n=h_{n} \circ h_{(\tilde {v}_{0})}\circ \cdots \circ h_{(\tilde {v}_{k})}$
satisfies:
$\tilde {h}_n=h_{n} \circ h_{(\tilde {v}_{0})}\circ \cdots \circ h_{(\tilde {v}_{k})}$
satisfies:
-
•

-
•
 $\operatorname {\mathrm {Sgn}}_{(i)}(h_{n},S_{Y_0}(w))=1 \text { for all } w\in B_T(\gamma ,n+2r)\cap V_{t_0};$
$\operatorname {\mathrm {Sgn}}_{(i)}(h_{n},S_{Y_0}(w))=1 \text { for all } w\in B_T(\gamma ,n+2r)\cap V_{t_0};$
-
•
 $\operatorname {\mathrm {Sgn}}_{(i)}(h_{n},S_{Y_1}(w))=1 \text { for all } w\in B_T(\gamma ,n-1)\cap V_{t_1}.$
$\operatorname {\mathrm {Sgn}}_{(i)}(h_{n},S_{Y_1}(w))=1 \text { for all } w\in B_T(\gamma ,n-1)\cap V_{t_1}.$
Now, let
![]() $\{w_0,\ldots ,w_m\}$
be the set of vertices
$\{w_0,\ldots ,w_m\}$
be the set of vertices
![]() $w\in B_T(\gamma ,n)\cap V_{t_1}$
such that
$w\in B_T(\gamma ,n)\cap V_{t_1}$
such that
![]() $\operatorname {\mathrm {Sgn}}_{(i)}(\tilde {h}_n,S_{Y_1}(w))=-1$
. For each
$\operatorname {\mathrm {Sgn}}_{(i)}(\tilde {h}_n,S_{Y_1}(w))=-1$
. For each
![]() $j=0,1,\ldots ,m$
, choose
$j=0,1,\ldots ,m$
, choose
![]() $v_{j}\in \bigcap _{w\in B_T(\gamma ,n)-\{w_j\}} T(w_{j},w)$
such that
$v_{j}\in \bigcap _{w\in B_T(\gamma ,n)-\{w_j\}} T(w_{j},w)$
such that
![]() $d(v_{j},w_{j})=\max (Y_1)$
. Since
$d(v_{j},w_{j})=\max (Y_1)$
. Since
![]() $\max (Y_0)+2r\leq \max (Y_1)$
, notice from Remark 3.4 that
$\max (Y_0)+2r\leq \max (Y_1)$
, notice from Remark 3.4 that
![]() $v_j\not \in S_{Y_0}(w)$
for every
$v_j\not \in S_{Y_0}(w)$
for every
![]() $w\in B_T(\gamma ,n+2r)\cap V_{t_0}$
and
$w\in B_T(\gamma ,n+2r)\cap V_{t_0}$
and
![]() $v_j\not \in S_{Y_1}(w)$
for every
$v_j\not \in S_{Y_1}(w)$
for every
![]() $w\in B_T(\gamma ,n)\cap V_{t_1}-\{w_j\}$
. Just as before, notice that the automorphisms
$w\in B_T(\gamma ,n)\cap V_{t_1}-\{w_j\}$
. Just as before, notice that the automorphisms
![]() $h_{(v_{0})}, \ldots ,h_{(v_{m})}$
fix
$h_{(v_{0})}, \ldots ,h_{(v_{m})}$
fix
![]() $\mathcal {T}\cup \mathcal {T}'$
pointwise. In particular,
$\mathcal {T}\cup \mathcal {T}'$
pointwise. In particular,
![]() $h_{n+1}=\tilde {h}_{n} \circ h_{(v_{0})}\circ \cdots \circ h_{(v_{m})}$
satisfies:
$h_{n+1}=\tilde {h}_{n} \circ h_{(v_{0})}\circ \cdots \circ h_{(v_{m})}$
satisfies:
-
•

-
•
 $\operatorname {\mathrm {Sgn}}_{(i)}(h_{n+1},S_{Y_0}(w))=1 \text { for all } w\in B(\gamma ,n+2r)\cap V_{t_0};$
$\operatorname {\mathrm {Sgn}}_{(i)}(h_{n+1},S_{Y_0}(w))=1 \text { for all } w\in B(\gamma ,n+2r)\cap V_{t_0};$
-
•
 $\operatorname {\mathrm {Sgn}}_{(i)}(h_{n+1},S_{Y_1}(w))=1 \text { for all } w\in B(\gamma ,n)\cap V_{t_1}.$
$\operatorname {\mathrm {Sgn}}_{(i)}(h_{n+1},S_{Y_1}(w))=1 \text { for all } w\in B(\gamma ,n)\cap V_{t_1}.$
This proves that
![]() $\Omega _n$
is not empty. We now show that
$\Omega _n$
is not empty. We now show that
![]() $\Omega _n$
is compact for every integer
$\Omega _n$
is compact for every integer
![]() $n\geq 1$
. To this end, notice that
$n\geq 1$
. To this end, notice that
![]() $\Omega _n$
is a closed subset of
$\Omega _n$
is a closed subset of
![]() $\operatorname {\mathrm {Aut}}(T)^+$
and that
$\operatorname {\mathrm {Aut}}(T)^+$
and that
Since the right-hand side is a compact subset of
![]() $\operatorname {\mathrm {Aut}}(T)^+$
, the results follow.
$\operatorname {\mathrm {Aut}}(T)^+$
, the results follow.
Finally, we prove the result announced at the beginning of Section 4.3.
Theorem 4.10. The generic filtration
![]() $\mathcal {S}_{0}$
of
$\mathcal {S}_{0}$
of
![]() $G^+_{(i)}(Y_0,Y_1)$
factorises
$G^+_{(i)}(Y_0,Y_1)$
factorises
![]() $^+$
at every depth
$^+$
at every depth
![]() $l\geq 1$
.
$l\geq 1$
.
Proof. Let
![]() $G=G^+_{(i)}(Y_0,Y_1)$
. To prove that
$G=G^+_{(i)}(Y_0,Y_1)$
. To prove that
![]() $\mathcal {S}_0$
factorises
$\mathcal {S}_0$
factorises
![]() $^+$
at depth
$^+$
at depth
![]() $l\geq 1$
, we successively check the three conditions of Definition 4.3.
$l\geq 1$
, we successively check the three conditions of Definition 4.3.
First, we must prove that for every U in the conjugacy class of an element of
![]() $\mathcal {S}_0\lbrack l \rbrack $
and every subgroup V in the conjugacy class of an element of
$\mathcal {S}_0\lbrack l \rbrack $
and every subgroup V in the conjugacy class of an element of
![]() $\mathcal {S}_0$
with
$\mathcal {S}_0$
with
![]() $V \not \subseteq U$
, there exists a W in the conjugacy class of an element of
$V \not \subseteq U$
, there exists a W in the conjugacy class of an element of
![]() $\mathcal {S}_0\lbrack l -1\rbrack $
such that
$\mathcal {S}_0\lbrack l -1\rbrack $
such that
Let U and V be as above. By the definition of
![]() $\mathcal {S}_0$
and since
$\mathcal {S}_0$
and since
![]() $\mathfrak {T}_0$
is stable under the action of G, there exist two subtrees
$\mathfrak {T}_0$
is stable under the action of G, there exist two subtrees
![]() $\mathcal {T},\mathcal {T}'\in \mathfrak {T}_0$
such that
$\mathcal {T},\mathcal {T}'\in \mathfrak {T}_0$
such that
![]() $U=\mathrm {Fix}_G(\mathcal {T})$
and
$U=\mathrm {Fix}_G(\mathcal {T})$
and
![]() $V=\mathrm {Fix}_G(\mathcal {T}')$
. In particular,
$V=\mathrm {Fix}_G(\mathcal {T}')$
. In particular,
![]() $\mathcal {T}'= B_T(o,r)$
, where o is either a vertex or an edge of T and r is a nonnegative integer. Let v be the vertex of
$\mathcal {T}'= B_T(o,r)$
, where o is either a vertex or an edge of T and r is a nonnegative integer. Let v be the vertex of
![]() $\mathcal {T}$
at maximal distance from o and notice since
$\mathcal {T}$
at maximal distance from o and notice since
![]() $V \not \subseteq U$
that
$V \not \subseteq U$
that
![]() $d_T(v,o)> r$
. Now let
$d_T(v,o)> r$
. Now let
![]() $\gamma $
be an infinite geodesic ray starting at v and containing o, let
$\gamma $
be an infinite geodesic ray starting at v and containing o, let
![]() $\mathcal {P}$
be the tree centred at
$\mathcal {P}$
be the tree centred at
![]() $\gamma (d_T(v,o) + l)$
of radius
$\gamma (d_T(v,o) + l)$
of radius
![]() $r+l$
and let
$r+l$
and let
![]() $V'=\mathrm {Fix}_G(\mathcal {P})$
. By construction, one has that
$V'=\mathrm {Fix}_G(\mathcal {P})$
. By construction, one has that
![]() $\mathcal {T}'\subseteq \mathcal {P}$
so that
$\mathcal {T}'\subseteq \mathcal {P}$
so that
![]() $V'\subseteq V$
. Furthermore,
$V'\subseteq V$
. Furthermore,
![]() $V'$
has depth greater than l and since
$V'$
has depth greater than l and since
![]() $v\not \in \mathcal {P}$
, Lemma 4.6 ensures that
$v\not \in \mathcal {P}$
, Lemma 4.6 ensures that
![]() $V'\not \subseteq U$
. Now, Proposition 4.7 ensures the existence of a subgroup
$V'\not \subseteq U$
. Now, Proposition 4.7 ensures the existence of a subgroup
![]() $W\in \mathcal {S}_0\lbrack l-1\rbrack $
such that
$W\in \mathcal {S}_0\lbrack l-1\rbrack $
such that
This proves the first condition.
Next, we must prove that
![]() $N_{G}(U, V)= \{g\in {G} \mid g^{-1}Vg\subseteq U\}$
is compact for every V in the conjugacy class of an element of
$N_{G}(U, V)= \{g\in {G} \mid g^{-1}Vg\subseteq U\}$
is compact for every V in the conjugacy class of an element of
![]() $\mathcal {S}_0$
. Just as before, notice that there exists a
$\mathcal {S}_0$
. Just as before, notice that there exists a
![]() $\mathcal {T}'\in \mathfrak {T}_0$
such that
$\mathcal {T}'\in \mathfrak {T}_0$
such that
![]() $V = \mathrm {Fix}_G(\mathcal {T}')$
. Since G satisfies the hypothesis (H0), notice that
$V = \mathrm {Fix}_G(\mathcal {T}')$
. Since G satisfies the hypothesis (H0), notice that
 $$ \begin{align*} N_{G}(U, V)&= \{g\in G \mid g^{-1}Vg\subseteq U\}=\{g\in G \mid g^{-1}\mathrm{Fix}_G(\mathcal{T}')g\subseteq \mathrm{Fix}_G(\mathcal{T})\}\\ &=\{g\in G \mid \mathrm{Fix}_G(g^{-1}\mathcal{T}')\subseteq \mathrm{Fix}_G(\mathcal{T})\}= \{g\in G \mid g\mathcal{T}\subseteq \mathcal{T}'\}. \end{align*} $$
$$ \begin{align*} N_{G}(U, V)&= \{g\in G \mid g^{-1}Vg\subseteq U\}=\{g\in G \mid g^{-1}\mathrm{Fix}_G(\mathcal{T}')g\subseteq \mathrm{Fix}_G(\mathcal{T})\}\\ &=\{g\in G \mid \mathrm{Fix}_G(g^{-1}\mathcal{T}')\subseteq \mathrm{Fix}_G(\mathcal{T})\}= \{g\in G \mid g\mathcal{T}\subseteq \mathcal{T}'\}. \end{align*} $$
In particular, since both
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}'$
are finite subtrees of T,
$\mathcal {T}'$
are finite subtrees of T,
![]() $N_G(U,V)$
is a compact subset of G which proves the second condition.
$N_G(U,V)$
is a compact subset of G which proves the second condition.
Finally, we must prove for every W in the conjugacy class of an element of
![]() $\mathcal {S}_0\lbrack l-1\rbrack $
with
$\mathcal {S}_0\lbrack l-1\rbrack $
with
![]() $U\subseteq W$
that
$U\subseteq W$
that
For the same reasons as before, there exists
![]() $\mathcal {R}\in \mathfrak {T}_0$
such that
$\mathcal {R}\in \mathfrak {T}_0$
such that
![]() $W= \mathrm {Fix}_G(\mathcal {R})$
. Furthermore, since
$W= \mathrm {Fix}_G(\mathcal {R})$
. Furthermore, since
![]() $U\subseteq W$
and since G satisfies the hypothesis (H0), notice that
$U\subseteq W$
and since G satisfies the hypothesis (H0), notice that
![]() $\mathcal {R}\subseteq \mathcal {T}$
. Moreover, since
$\mathcal {R}\subseteq \mathcal {T}$
. Moreover, since
![]() $\mathrm {Fix}_G(\mathcal {R})$
has depth
$\mathrm {Fix}_G(\mathcal {R})$
has depth
![]() $l-1$
, notice that
$l-1$
, notice that
![]() $\mathcal {R}$
contains every interior vertex of
$\mathcal {R}$
contains every interior vertex of
![]() $\mathcal {T}$
. Since G is unimodular and satisfies hypothesis (H0), this implies that
$\mathcal {T}$
. Since G is unimodular and satisfies hypothesis (H0), this implies that
 $$ \begin{align*} \mathrm{Fix}_G(\mathcal{R})&\subseteq \{h\in G \mid h\mathcal{T}\subseteq \mathcal{T}\}= \{h\in G \mid \mathrm{Fix}_G(\mathcal{T})\subseteq\mathrm{Fix}_G(h\mathcal{T})\}\\ &=\{h\in G \mid h^{-1}\mathrm{Fix}_G(\mathcal{T})h\subseteq\mathrm{Fix}_G(\mathcal{T})\}= N_G(U,U), \end{align*} $$
$$ \begin{align*} \mathrm{Fix}_G(\mathcal{R})&\subseteq \{h\in G \mid h\mathcal{T}\subseteq \mathcal{T}\}= \{h\in G \mid \mathrm{Fix}_G(\mathcal{T})\subseteq\mathrm{Fix}_G(h\mathcal{T})\}\\ &=\{h\in G \mid h^{-1}\mathrm{Fix}_G(\mathcal{T})h\subseteq\mathrm{Fix}_G(\mathcal{T})\}= N_G(U,U), \end{align*} $$
which proves the third condition.
4.4 Description of cuspidal representations
The purpose of this section is to give a description of the cuspidal representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
. This is done by Theorem 4.12 below but requires some preliminaries. We refer to [Reference SemalSem23] for proofs and details of the formalism.
$G_{(i)}^+(Y_0,Y_1)$
. This is done by Theorem 4.12 below but requires some preliminaries. We refer to [Reference SemalSem23] for proofs and details of the formalism.
Let G be a nondiscrete unimodular totally disconnected locally compact group G and let
![]() $\mathcal {S}$
be a generic filtration of G factorising
$\mathcal {S}$
be a generic filtration of G factorising
![]() $^+$
at depth l. Then, for every irreducible representation
$^+$
at depth l. Then, for every irreducible representation
![]() $\pi $
of G at depth l, [Reference SemalSem23, Theorem A] ensures the existence of a unique conjugacy class
$\pi $
of G at depth l, [Reference SemalSem23, Theorem A] ensures the existence of a unique conjugacy class
![]() $C_\pi \in \mathcal {F}_{\mathcal {S}}=\{\mathcal {C}(U)\mid U\in \mathcal {S}\}$
at height l such that
$C_\pi \in \mathcal {F}_{\mathcal {S}}=\{\mathcal {C}(U)\mid U\in \mathcal {S}\}$
at height l such that
![]() $\pi $
admits nonzero U-invariant vectors for any
$\pi $
admits nonzero U-invariant vectors for any
![]() $U\in C_\pi $
. The conjugacy class
$U\in C_\pi $
. The conjugacy class
![]() $C_\pi $
is called the seed of
$C_\pi $
is called the seed of
![]() $\pi $
. We define the group of automorphisms
$\pi $
. We define the group of automorphisms
![]() $\operatorname {\mathrm {Aut}}_{G}(C)$
of the seed C as the quotient
$\operatorname {\mathrm {Aut}}_{G}(C)$
of the seed C as the quotient
![]() $N_G(U)/U$
corresponding to any
$N_G(U)/U$
corresponding to any
![]() $U\in C$
. This group
$U\in C$
. This group
![]() $\operatorname {\mathrm {Aut}}_{G}(C)$
is finite and does not depend on our choice of
$\operatorname {\mathrm {Aut}}_{G}(C)$
is finite and does not depend on our choice of
![]() $U\in C$
up to isomorphism. Now, let
$U\in C$
up to isomorphism. Now, let
![]() $p_{U}: N_G(U)\mapsto N_G(U)/U$
denote the quotient map, let
$p_{U}: N_G(U)\mapsto N_G(U)/U$
denote the quotient map, let
and set
Notice that
![]() $\mathfrak {H}_{\mathcal {S}}(C)$
does not depend on our choice of representative
$\mathfrak {H}_{\mathcal {S}}(C)$
does not depend on our choice of representative
![]() $U\in C$
.
$U\in C$
.
Definition 4.11. An irreducible representation
![]() $\omega $
of
$\omega $
of
![]() $\operatorname {\mathrm {Aut}}_{G}(C)$
is called
$\operatorname {\mathrm {Aut}}_{G}(C)$
is called
![]() $\mathcal {S}$
-standard if it has no nonzero H-invariant vector for any
$\mathcal {S}$
-standard if it has no nonzero H-invariant vector for any
![]() $H\in \mathfrak {H}_{\mathcal {S}}(C)$
.
$H\in \mathfrak {H}_{\mathcal {S}}(C)$
.
The importance of this notion is given by [Reference SemalSem23, Theorem A], which ensures that the irreducible representations of G at depth l with seed C are obtained from the
![]() $\mathcal {S}$
-standard representations of
$\mathcal {S}$
-standard representations of
![]() $\operatorname {\mathrm {Aut}}_G(C)$
when
$\operatorname {\mathrm {Aut}}_G(C)$
when
![]() $\mathcal {S}$
factorises
$\mathcal {S}$
factorises
![]() $^+$
at depth l. More precisely, we recall that every irreducible representation
$^+$
at depth l. More precisely, we recall that every irreducible representation
![]() $\omega $
of
$\omega $
of
![]() $\operatorname {\mathrm {Aut}}_G(C)\cong N_G(U)/U$
can be lifted to an irreducible representation
$\operatorname {\mathrm {Aut}}_G(C)\cong N_G(U)/U$
can be lifted to an irreducible representation
![]() $\omega \circ p_U$
of
$\omega \circ p_U$
of
![]() $N_G(U)$
with U acting trivially and with representation space
$N_G(U)$
with U acting trivially and with representation space
![]() $\mathcal {H}_{\omega }$
. The lifted representation can then be induced to G. The resulting representation
$\mathcal {H}_{\omega }$
. The lifted representation can then be induced to G. The resulting representation
is an irreducible representation of G with seed
![]() $\mathcal {C}(U)$
. Conversely, if
$\mathcal {C}(U)$
. Conversely, if
![]() $\pi $
is an irreducible representation of G with seed C, notice that
$\pi $
is an irreducible representation of G with seed C, notice that
![]() $\mathcal {H}_{\pi }^{U}$
is a nonzero
$\mathcal {H}_{\pi }^{U}$
is a nonzero
![]() $N_G(U)$
-invariant subspace of
$N_G(U)$
-invariant subspace of
![]() $\mathcal {H}_{\pi }$
for every
$\mathcal {H}_{\pi }$
for every
![]() $U\in C$
. In particular, the restriction
$U\in C$
. In particular, the restriction ![]() is a representation of
is a representation of
![]() $N_G(U)$
whose restriction to U is trivial. This representation passes to the quotient group
$N_G(U)$
whose restriction to U is trivial. This representation passes to the quotient group
![]() $N_G(U)/U$
and defines an
$N_G(U)/U$
and defines an
![]() $\mathcal {S}$
-standard representation
$\mathcal {S}$
-standard representation
![]() $\omega _\pi $
of
$\omega _\pi $
of
![]() $\operatorname {\mathrm {Aut}}_{G}(C)$
.
$\operatorname {\mathrm {Aut}}_{G}(C)$
.
We now come back to the case in which we are interested. Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 4$
, let
$d_0,d_1\geq 4$
, let
![]() $V(T)=V_0\sqcup V_1$
be the associated bipartition and let
$V(T)=V_0\sqcup V_1$
be the associated bipartition and let
Let i be a legal colouring of T, let
![]() $Y_0,Y_1\subseteq \mathbb N$
be two finite subsets and consider the group
$Y_0,Y_1\subseteq \mathbb N$
be two finite subsets and consider the group
![]() $G_{(i)}^+(Y_0,Y_1)$
. Let
$G_{(i)}^+(Y_0,Y_1)$
. Let
![]() $G=G_{(i)}^+(Y_0,Y_1)$
. We have shown in Sections 4.2 and 4.3 that
$G=G_{(i)}^+(Y_0,Y_1)$
. We have shown in Sections 4.2 and 4.3 that
is a generic filtration of
![]() $G_{(i)}^+(Y_0,Y_1)$
that factorises
$G_{(i)}^+(Y_0,Y_1)$
that factorises
![]() $^+$
at all depths
$^+$
at all depths
![]() $l\geq 1$
. In particular, [Reference SemalSem23, Theorem A] provides a bijective correspondence between irreducible representations of
$l\geq 1$
. In particular, [Reference SemalSem23, Theorem A] provides a bijective correspondence between irreducible representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
at depth l with seed
$G_{(i)}^+(Y_0,Y_1)$
at depth l with seed
![]() $C \in \mathcal {F}_{\mathcal {S}_0}$
and the
$C \in \mathcal {F}_{\mathcal {S}_0}$
and the
![]() $\mathcal {S}_0$
-standard representations of
$\mathcal {S}_0$
-standard representations of
![]() $\operatorname {\mathrm {Aut}}_G(C)$
. We start by identifying these seeds and show that the cuspidal representations of G are precisely the irreducible representations of G at depth
$\operatorname {\mathrm {Aut}}_G(C)$
. We start by identifying these seeds and show that the cuspidal representations of G are precisely the irreducible representations of G at depth
![]() $l\geq 1$
with respect to
$l\geq 1$
with respect to
![]() $\mathcal {S}_0$
. In the light of Lemma 4.5, we consider the partition
$\mathcal {S}_0$
. In the light of Lemma 4.5, we consider the partition
![]() $\mathfrak {T}_0=\bigsqcup _{l\in \mathbb N}\mathfrak {T}_0\lbrack l\rbrack $
where:
$\mathfrak {T}_0=\bigsqcup _{l\in \mathbb N}\mathfrak {T}_0\lbrack l\rbrack $
where:
-
•
 $\mathfrak {T}_0\lbrack l\rbrack = \{B_T(e,\tfrac {l}{2})\mid e\in E(T)\}$
if l is even;
$\mathfrak {T}_0\lbrack l\rbrack = \{B_T(e,\tfrac {l}{2})\mid e\in E(T)\}$
if l is even; -
•
 $\mathfrak {T}_0\lbrack l \rbrack =\{ B_T(v,(({l+1})/{2}))\mid v\in V(T)\}$
if l is odd.
$\mathfrak {T}_0\lbrack l \rbrack =\{ B_T(v,(({l+1})/{2}))\mid v\in V(T)\}$
if l is odd.
Notice that for all
![]() $l\in \mathbb N$
,
$l\in \mathbb N$
,
![]() $\mathfrak {T}_0\lbrack l\rbrack $
is stable under the action of G. Furthermore, notice that if l is even, or if l is odd and G is transitive on the vertices, the set
$\mathfrak {T}_0\lbrack l\rbrack $
is stable under the action of G. Furthermore, notice that if l is even, or if l is odd and G is transitive on the vertices, the set
![]() $\mathfrak {T}_0\lbrack l\rbrack $
consists of a single G-orbit. However, if l is odd and G has two orbits of vertices, notice that the set
$\mathfrak {T}_0\lbrack l\rbrack $
consists of a single G-orbit. However, if l is odd and G has two orbits of vertices, notice that the set
![]() $\mathfrak {T}_0\lbrack l\rbrack $
consists of two G-orbits, namely
$\mathfrak {T}_0\lbrack l\rbrack $
consists of two G-orbits, namely
![]() $\{B_T(v,(({l+1})/{2}))\mid v\in V_0\}$
and
$\{B_T(v,(({l+1})/{2}))\mid v\in V_0\}$
and
![]() $\{B_T(v,(({l+1})/{2}))\mid v\in V_1\}$
. In particular, in light of Lemma 4.6, there are either one or two elements of
$\{B_T(v,(({l+1})/{2}))\mid v\in V_1\}$
. In particular, in light of Lemma 4.6, there are either one or two elements of
![]() $\mathcal {F}_{\mathcal {S}_0}=\{\mathcal {C}(U)\mid U\in \mathcal {S}_0\}$
at height l and each such element is of the form
$\mathcal {F}_{\mathcal {S}_0}=\{\mathcal {C}(U)\mid U\in \mathcal {S}_0\}$
at height l and each such element is of the form
where
![]() $\mathcal {O}$
is a G-orbit of
$\mathcal {O}$
is a G-orbit of
![]() $\mathfrak {T}_0\lbrack l \rbrack $
. We deduce easily that the irreducible representations of
$\mathfrak {T}_0\lbrack l \rbrack $
. We deduce easily that the irreducible representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
at depth
$G_{(i)}^+(Y_0,Y_1)$
at depth
![]() $l\geq 1$
with respect to
$l\geq 1$
with respect to
![]() $\mathcal {S}_0$
are the cuspidal representations of G. Indeed,
$\mathcal {S}_0$
are the cuspidal representations of G. Indeed,
![]() $\pi $
is an irreducible representation at depth
$\pi $
is an irreducible representation at depth
![]() $l\geq 1$
with respect to
$l\geq 1$
with respect to
![]() $\mathcal {S}_0$
if and only if
$\mathcal {S}_0$
if and only if
![]() $\pi $
does not admit a nonzero V-invariant vector for any V in a conjugacy class C at depth
$\pi $
does not admit a nonzero V-invariant vector for any V in a conjugacy class C at depth
![]() $0$
, that is, for any
$0$
, that is, for any
![]() $V\in \{\mathrm {Fix}_G(e)\mid e\in E(T)\}$
. Now, let
$V\in \{\mathrm {Fix}_G(e)\mid e\in E(T)\}$
. Now, let
![]() $\pi $
be a cuspidal representation of G, let
$\pi $
be a cuspidal representation of G, let
![]() $C_\pi \in \mathcal {F}_{\mathcal {S}_0}$
be the seed of
$C_\pi \in \mathcal {F}_{\mathcal {S}_0}$
be the seed of
![]() $\pi $
, let
$\pi $
, let
![]() $U\in C_\pi $
and let
$U\in C_\pi $
and let
![]() $\mathcal {T}\in \mathfrak {T}_0$
be such that
$\mathcal {T}\in \mathfrak {T}_0$
be such that
![]() $U=\mathrm {Fix}_G(\mathcal {T})$
. Since
$U=\mathrm {Fix}_G(\mathcal {T})$
. Since
![]() $\mathcal {S}_0$
factorises
$\mathcal {S}_0$
factorises
![]() $^+$
at all depths
$^+$
at all depths
![]() $l\geq 1$
, [Reference SemalSem23, Theorem A] ensures that
$l\geq 1$
, [Reference SemalSem23, Theorem A] ensures that
![]() $\pi $
is induced from an irreducible representation of
$\pi $
is induced from an irreducible representation of
![]() $N_G(U)$
that passes to the quotient
$N_G(U)$
that passes to the quotient
![]() ${\operatorname {\mathrm {Aut}}_G(C_\pi )\cong N_G(U)/U}$
. Furthermore, since G satisfies hypothesis (H0), notice that
${\operatorname {\mathrm {Aut}}_G(C_\pi )\cong N_G(U)/U}$
. Furthermore, since G satisfies hypothesis (H0), notice that
 $$ \begin{align*} N_G(U)= \{g\in G\mid gUg^{-1}=U\} &=\{g\in G\mid g\mathrm{Fix}_G(\mathcal{T})g^{-1}=\mathrm{Fix}_G(\mathcal{T})\}\\ &=\{g\in G\mid \mathrm{Fix}_G(g\mathcal{T})=\mathrm{Fix}_G(\mathcal{T})\}\\ &=\{g\in G\mid g\mathcal{T}=\mathcal{T}\}=\operatorname{\mathrm{Stab}}_G(\mathcal{T}) \end{align*} $$
$$ \begin{align*} N_G(U)= \{g\in G\mid gUg^{-1}=U\} &=\{g\in G\mid g\mathrm{Fix}_G(\mathcal{T})g^{-1}=\mathrm{Fix}_G(\mathcal{T})\}\\ &=\{g\in G\mid \mathrm{Fix}_G(g\mathcal{T})=\mathrm{Fix}_G(\mathcal{T})\}\\ &=\{g\in G\mid g\mathcal{T}=\mathcal{T}\}=\operatorname{\mathrm{Stab}}_G(\mathcal{T}) \end{align*} $$
is exactly the stabiliser of
![]() $\mathcal {T}$
in
$\mathcal {T}$
in
![]() $G_{(i)}^+(Y_0,Y_1)$
. In particular,
$G_{(i)}^+(Y_0,Y_1)$
. In particular,
![]() $\operatorname {\mathrm {Aut}}_G(C_\pi )$
can be identified with the automorphism group of
$\operatorname {\mathrm {Aut}}_G(C_\pi )$
can be identified with the automorphism group of
![]() $\mathcal {T}$
obtained by restricting the action of
$\mathcal {T}$
obtained by restricting the action of
![]() $\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
to
$\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
to
![]() $\mathcal {T}$
. Moreover, since G satisfies hypothesis (H0), notice that
$\mathcal {T}$
. Moreover, since G satisfies hypothesis (H0), notice that
and
is the set of fixators (in
![]() $\operatorname {\mathrm {Aut}}_G(C_\pi )$
) of subtrees
$\operatorname {\mathrm {Aut}}_G(C_\pi )$
) of subtrees
![]() $\mathcal {R}\in \mathcal {T}_0$
satisfying
$\mathcal {R}\in \mathcal {T}_0$
satisfying
![]() $\mathcal {R}\subsetneq \mathcal {T}$
and that are maximal for this property. In particular, the
$\mathcal {R}\subsetneq \mathcal {T}$
and that are maximal for this property. In particular, the
![]() $\mathcal {S}_0$
-standard representations of
$\mathcal {S}_0$
-standard representations of
![]() $\operatorname {\mathrm {Aut}}_G(C_\pi )$
are the irreducible representations of the group of automorphisms of
$\operatorname {\mathrm {Aut}}_G(C_\pi )$
are the irreducible representations of the group of automorphisms of
![]() $\mathcal {T}$
obtained by restricting the action of
$\mathcal {T}$
obtained by restricting the action of
![]() $\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
and that do not admit any nonzero invariant vector for the fixator of any subtree
$\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
and that do not admit any nonzero invariant vector for the fixator of any subtree
![]() $\mathcal {R}$
of
$\mathcal {R}$
of
![]() $\mathcal {T}$
that belongs to
$\mathcal {T}$
that belongs to
![]() $\mathfrak {T}_0$
and is maximal for this property. The above discussion together with [Reference SemalSem23, Theorem A] leads to the following description of the cuspidal representations of
$\mathfrak {T}_0$
and is maximal for this property. The above discussion together with [Reference SemalSem23, Theorem A] leads to the following description of the cuspidal representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
.
$G_{(i)}^+(Y_0,Y_1)$
.
Theorem 4.12. Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 4$
, let i be a legal colouring of T, let
$d_0,d_1\geq 4$
, let i be a legal colouring of T, let
![]() $Y_0,Y_1\subseteq \mathbb N$
be two finite subsets, let
$Y_0,Y_1\subseteq \mathbb N$
be two finite subsets, let
![]() $G=G_{(i)}^+(Y_0,Y_1)$
, consider the generic filtration
$G=G_{(i)}^+(Y_0,Y_1)$
, consider the generic filtration
![]() $\mathcal {S}_0$
of G (defined in Section 4.2) and let us use the above notation. Then, the cuspidal representations of G are exactly the irreducible representations at depth
$\mathcal {S}_0$
of G (defined in Section 4.2) and let us use the above notation. Then, the cuspidal representations of G are exactly the irreducible representations at depth
![]() $l\geq 1$
with respect to
$l\geq 1$
with respect to
![]() $\mathcal {S}_{0}$
. Furthermore, if
$\mathcal {S}_{0}$
. Furthermore, if
![]() $\pi $
is a cuspidal representation at depth l, we have the following.
$\pi $
is a cuspidal representation at depth l, we have the following.
-
•
 $\pi $
has no nonzero
$\pi $
has no nonzero
 $\mathrm {Fix}_G(\mathcal {R})$
-invariant vector for any
$\mathrm {Fix}_G(\mathcal {R})$
-invariant vector for any
 $\mathcal {R}\in \bigsqcup _{r<l}\mathfrak {T}_0\lbrack r\rbrack $
.
$\mathcal {R}\in \bigsqcup _{r<l}\mathfrak {T}_0\lbrack r\rbrack $
. -
• There exists a unique conjugacy class
 $C_\pi \in \mathcal {F}_{\mathcal {S}_0}$
at height l such that
$C_\pi \in \mathcal {F}_{\mathcal {S}_0}$
at height l such that
 $\pi $
admits a nonzero U-invariant vector for any (hence for all)
$\pi $
admits a nonzero U-invariant vector for any (hence for all)
 $U\in C_\pi $
. Equivalently, there exists a unique G-orbit
$U\in C_\pi $
. Equivalently, there exists a unique G-orbit
 $\mathcal {O}$
of
$\mathcal {O}$
of
 $\mathfrak {T}_0\lbrack l \rbrack $
such that
$\mathfrak {T}_0\lbrack l \rbrack $
such that
 $\pi $
admits a nonzero
$\pi $
admits a nonzero
 $\mathrm {Fix}_G(\mathcal {T})$
-invariant vector for any (hence for all)
$\mathrm {Fix}_G(\mathcal {T})$
-invariant vector for any (hence for all)
 $\mathcal {T}\in \mathcal {O}$
. Furthermore,
$\mathcal {T}\in \mathcal {O}$
. Furthermore,
 $\mathcal {O}$
is the only orbit of
$\mathcal {O}$
is the only orbit of
 $\mathfrak {T}_0$
under the action of G such that
$\mathfrak {T}_0$
under the action of G such that
 $C_\pi =\{\mathrm {Fix}_G(\mathcal {T})\mid \mathcal {T}\in \mathcal {O}\}$
.
$C_\pi =\{\mathrm {Fix}_G(\mathcal {T})\mid \mathcal {T}\in \mathcal {O}\}$
. -
• If
 $\mathcal {O}$
is the unique G-orbit of
$\mathcal {O}$
is the unique G-orbit of
 $\mathfrak {T}_0\lbrack l \rbrack $
corresponding to
$\mathfrak {T}_0\lbrack l \rbrack $
corresponding to
 $\pi $
and if
$\pi $
and if
 $\mathcal {T}\in \mathcal {O}$
,
$\mathcal {T}\in \mathcal {O}$
,
 $\pi $
admits a nonzero diagonal matrix coefficient supported in
$\pi $
admits a nonzero diagonal matrix coefficient supported in
 $\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
. In particular,
$\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
. In particular,
 $\pi $
is square-integrable and its equivalence class is isolated in the unitary dual
$\pi $
is square-integrable and its equivalence class is isolated in the unitary dual
 $\widehat {G}$
for the Fell topology.
$\widehat {G}$
for the Fell topology.
Furthermore for each
![]() $C\in \mathcal {F}_{\mathcal {S}_0}$
at height
$C\in \mathcal {F}_{\mathcal {S}_0}$
at height
![]() $l\geq 1$
with corresponding G-orbit
$l\geq 1$
with corresponding G-orbit
![]() $\mathcal {O}$
in
$\mathcal {O}$
in
![]() $\mathfrak {T}_0\lbrack l \rbrack $
, that is,
$\mathfrak {T}_0\lbrack l \rbrack $
, that is,
![]() $C=\{\mathrm {Fix}_G(\mathcal {T})\mid \mathcal {T}\in \mathcal {O}\}$
, there exists a bijective correspondence between the equivalence classes of irreducible representations of G with seed C and the equivalence classes of
$C=\{\mathrm {Fix}_G(\mathcal {T})\mid \mathcal {T}\in \mathcal {O}\}$
, there exists a bijective correspondence between the equivalence classes of irreducible representations of G with seed C and the equivalence classes of
![]() $\mathcal {S}_0$
-standard representations of
$\mathcal {S}_0$
-standard representations of
![]() $\operatorname {\mathrm {Aut}}_G(C)$
. More precisely, for every
$\operatorname {\mathrm {Aut}}_G(C)$
. More precisely, for every
![]() $\mathcal {T}\in \mathcal {O}$
, the following hold.
$\mathcal {T}\in \mathcal {O}$
, the following hold.
-
(1) If
 $\pi $
is a cuspidal representation of G with seed C,
$\pi $
is a cuspidal representation of G with seed C,
 $(\omega _\pi , \mathcal {H}_{\pi }^{\mathrm {Fix}_G(\mathcal {T})})$
is an
$(\omega _\pi , \mathcal {H}_{\pi }^{\mathrm {Fix}_G(\mathcal {T})})$
is an
 $\mathcal {S}_0$
-standard representation of
$\mathcal {S}_0$
-standard representation of
 $\operatorname {\mathrm {Aut}}_{G}(C)$
such that
$\operatorname {\mathrm {Aut}}_{G}(C)$
such that  $$ \begin{align*} \pi \cong T(\mathrm{Fix}_G(\mathcal{T}),\omega_\pi)=\operatorname{\mathrm{Ind}}_{\operatorname{\mathrm{Stab}}_G(\mathcal{T})}^{G}(\omega_\pi \circ p_{\mathrm{Fix}_G(\mathcal{T})}). \end{align*} $$
$$ \begin{align*} \pi \cong T(\mathrm{Fix}_G(\mathcal{T}),\omega_\pi)=\operatorname{\mathrm{Ind}}_{\operatorname{\mathrm{Stab}}_G(\mathcal{T})}^{G}(\omega_\pi \circ p_{\mathrm{Fix}_G(\mathcal{T})}). \end{align*} $$
-
(2) If
 $\omega $
is an
$\omega $
is an
 $\mathcal {S}_0$
-standard representation of
$\mathcal {S}_0$
-standard representation of
 $\operatorname {\mathrm {Aut}}_{G}(C)$
, the representation
$\operatorname {\mathrm {Aut}}_{G}(C)$
, the representation
 $T(\mathrm {Fix}_G(\mathcal {T}),\omega )$
is a cuspidal representation of G with seed in C.
$T(\mathrm {Fix}_G(\mathcal {T}),\omega )$
is a cuspidal representation of G with seed in C.
Furthermore, if
![]() $\omega _1$
and
$\omega _1$
and
![]() $\omega _2$
are
$\omega _2$
are
![]() $\mathcal {S}_0$
-standard representations of
$\mathcal {S}_0$
-standard representations of
![]() $\operatorname {\mathrm {Aut}}_{G}(C)$
, we have that
$\operatorname {\mathrm {Aut}}_{G}(C)$
, we have that
![]() $T(\mathrm {Fix}_G(\mathcal {T}),\omega _1)\cong T(\mathrm {Fix}_G(\mathcal {T}),\omega _2)$
if and only if
$T(\mathrm {Fix}_G(\mathcal {T}),\omega _1)\cong T(\mathrm {Fix}_G(\mathcal {T}),\omega _2)$
if and only if
![]() $\omega _1\cong \omega _2$
. In particular, the above two constructions are inverse of one another.
$\omega _1\cong \omega _2$
. In particular, the above two constructions are inverse of one another.
4.5 Existence of cuspidal representations
As in the previous sections, let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 4$
, let
$d_0,d_1\geq 4$
, let
![]() $V(T)=V_0\sqcup V_1$
be the associated bipartition and let
$V(T)=V_0\sqcup V_1$
be the associated bipartition and let
Let i be a legal colouring of T, let
![]() $Y_0,Y_1\subseteq \mathbb N$
be two finite subsets and consider the group
$Y_0,Y_1\subseteq \mathbb N$
be two finite subsets and consider the group
![]() $G_{(i)}^+(Y_0,Y_1)$
. Write
$G_{(i)}^+(Y_0,Y_1)$
. Write
![]() $G=G_{(i)}^+(Y_0,Y_1)$
if this leads to no confusion. We have shown in Sections 4.2 and 4.3 that
$G=G_{(i)}^+(Y_0,Y_1)$
if this leads to no confusion. We have shown in Sections 4.2 and 4.3 that
is a generic filtration of
![]() $G_{(i)}^+(Y_0,Y_1)$
factorising
$G_{(i)}^+(Y_0,Y_1)$
factorising
![]() $^+$
at all depths
$^+$
at all depths
![]() $l\geq 1$
. In particular, [Reference SemalSem23, Theorem A] provides a bijective correspondence between the irreducible representations of
$l\geq 1$
. In particular, [Reference SemalSem23, Theorem A] provides a bijective correspondence between the irreducible representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
at depth l with seed
$G_{(i)}^+(Y_0,Y_1)$
at depth l with seed
![]() $C \in \mathcal {F}_{\mathcal {S}_0}$
and the
$C \in \mathcal {F}_{\mathcal {S}_0}$
and the
![]() $\mathcal {S}_0$
-standard representations of
$\mathcal {S}_0$
-standard representations of
![]() $\operatorname {\mathrm {Aut}}_G(C)$
. This leads to a description of the cuspidal representations of
$\operatorname {\mathrm {Aut}}_G(C)$
. This leads to a description of the cuspidal representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
; see Theorem 4.12. However, none of these results yet ensures the existence of a cuspidal representation of
$G_{(i)}^+(Y_0,Y_1)$
; see Theorem 4.12. However, none of these results yet ensures the existence of a cuspidal representation of
![]() $G_{(i)}^+(Y_0,Y_1)$
. The purpose of this section is to prove the existence of a cuspidal representation with seed C for each conjugacy class
$G_{(i)}^+(Y_0,Y_1)$
. The purpose of this section is to prove the existence of a cuspidal representation with seed C for each conjugacy class
![]() $C\in \mathcal {F}_{\mathcal {S}_0}$
at height
$C\in \mathcal {F}_{\mathcal {S}_0}$
at height
![]() $l\geq 1$
. From the description of cuspidal representations of
$l\geq 1$
. From the description of cuspidal representations of
![]() $G^+_{(i)}(Y_0,Y_1)$
provided by Theorem 4.12, it is equivalent to prove the following theorem.
$G^+_{(i)}(Y_0,Y_1)$
provided by Theorem 4.12, it is equivalent to prove the following theorem.
Theorem 4.13. Let
![]() $G=G^+_{(i)}(Y_0,Y_1)$
and let
$G=G^+_{(i)}(Y_0,Y_1)$
and let
![]() $C\in \mathcal {F}_{\mathcal {S}_0}$
be a conjugacy class at height
$C\in \mathcal {F}_{\mathcal {S}_0}$
be a conjugacy class at height
![]() $l\geq 1$
. Then, there exists an
$l\geq 1$
. Then, there exists an
![]() ${\mathcal {S}_0}$
-standard representation of
${\mathcal {S}_0}$
-standard representation of
![]() $\operatorname {\mathrm {Aut}}_G(C)$
.
$\operatorname {\mathrm {Aut}}_G(C)$
.
The proof of this theorem is gathered in the following results. We start by recalling a result from [Reference SemalSem23].
Proposition 4.14 [Reference SemalSem23, Proposition
 $2.29$
].
$2.29$
].
Let T be a locally finite tree, let
![]() ${G\leq \operatorname {\mathrm {Aut}}(T)}$
be a closed subgroup, let
${G\leq \operatorname {\mathrm {Aut}}(T)}$
be a closed subgroup, let
![]() $\mathcal {T}$
be a finite subtree of T and let
$\mathcal {T}$
be a finite subtree of T and let
![]() $\{\mathcal {T}_1,\mathcal {T}_2,\ldots ,\mathcal {T}_s\}$
be a set of distinct finite subtrees of T contained in
$\{\mathcal {T}_1,\mathcal {T}_2,\ldots ,\mathcal {T}_s\}$
be a set of distinct finite subtrees of T contained in
![]() $\mathcal {T}$
such that
$\mathcal {T}$
such that
![]() $\mathcal {T}_i\cup \mathcal {T}_j=\mathcal {T}$
for every
$\mathcal {T}_i\cup \mathcal {T}_j=\mathcal {T}$
for every
![]() $i\not =j$
. Suppose that
$i\not =j$
. Suppose that
![]() $\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
acts by permutation on the set
$\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
acts by permutation on the set
![]() $\{\mathcal {T}_1,\mathcal {T}_2,\ldots ,\mathcal {T}_s\}$
and that
$\{\mathcal {T}_1,\mathcal {T}_2,\ldots ,\mathcal {T}_s\}$
and that
![]() $\mathrm {Fix}_G(\mathcal {T})\subsetneq \mathrm {Fix}_G(\mathcal {T}_i)\subsetneq \operatorname {\mathrm {Stab}}_G(\mathcal {T})$
. Then, there exists an irreducible representation of
$\mathrm {Fix}_G(\mathcal {T})\subsetneq \mathrm {Fix}_G(\mathcal {T}_i)\subsetneq \operatorname {\mathrm {Stab}}_G(\mathcal {T})$
. Then, there exists an irreducible representation of
![]() $\operatorname {\mathrm {Stab}}_G(\mathcal {T})/\mathrm {Fix}_G(\mathcal {T})$
without a nonzero
$\operatorname {\mathrm {Stab}}_G(\mathcal {T})/\mathrm {Fix}_G(\mathcal {T})$
without a nonzero
![]() $\mathrm {Fix}_G(\mathcal {T}_i)/\mathrm {Fix}_G(\mathcal {T})$
-invariant vector for every
$\mathrm {Fix}_G(\mathcal {T}_i)/\mathrm {Fix}_G(\mathcal {T})$
-invariant vector for every
![]() ${i=1,\ldots ,s}$
.
${i=1,\ldots ,s}$
.
The following proposition ensures the existence of
![]() ${\mathcal {S}_0}$
-standard representations of
${\mathcal {S}_0}$
-standard representations of
![]() $\operatorname {\mathrm {Aut}}_{G}(C)$
for every
$\operatorname {\mathrm {Aut}}_{G}(C)$
for every
![]() $C\in \mathcal {F}_{\mathcal {S}_0}$
with height
$C\in \mathcal {F}_{\mathcal {S}_0}$
with height
![]() $l\geq 2$
.
$l\geq 2$
.
Proposition 4.15. Let
![]() $G=G^+_{(i)}(Y_0,Y_1)$
and let
$G=G^+_{(i)}(Y_0,Y_1)$
and let
![]() $C\in \mathcal {F}_{\mathcal {S}_0}$
be a conjugacy class at height
$C\in \mathcal {F}_{\mathcal {S}_0}$
be a conjugacy class at height
![]() $l\geq 2$
. Then, there exists an
$l\geq 2$
. Then, there exists an
![]() ${\mathcal {S}_0}$
-standard representation of
${\mathcal {S}_0}$
-standard representation of
![]() $\operatorname {\mathrm {Aut}}_{G}(C)$
.
$\operatorname {\mathrm {Aut}}_{G}(C)$
.
Proof. Since
![]() $l\geq 2$
, Lemma 4.5 ensures the existence of a complete finite subtree
$l\geq 2$
, Lemma 4.5 ensures the existence of a complete finite subtree
![]() $\mathcal {T}$
of T containing a ball of radius
$\mathcal {T}$
of T containing a ball of radius
![]() $1$
around an edge such that
$1$
around an edge such that
![]() $C=\mathcal {C}(\mathrm { Fix}_{G}(B_T(e,r)))$
. Furthermore, as observed in Section 4.4, we have that
$C=\mathcal {C}(\mathrm { Fix}_{G}(B_T(e,r)))$
. Furthermore, as observed in Section 4.4, we have that
![]() $\operatorname {\mathrm {Aut}}_G(C)\cong \operatorname {\mathrm {Stab}}_G(\mathcal {T})/\mathrm {Fix}_G(\mathcal {T})$
and
$\operatorname {\mathrm {Aut}}_G(C)\cong \operatorname {\mathrm {Stab}}_G(\mathcal {T})/\mathrm {Fix}_G(\mathcal {T})$
and
 $$ \begin{align*} \mathfrak{H}_{\mathcal{S}_0}(\mathrm{Fix}_G(\mathcal{T}))&=\{\mathrm{Fix}_G(\mathcal{R})/\mathrm{Fix}_G(\mathcal{T})\mid \mathcal{R}\in \mathfrak{T}_0, \mathcal{R}\subsetneq \mathcal{T} \\ &\qquad\,\mbox{and } \mathcal{R}\mbox{ is maximal for this property}\}. \end{align*} $$
$$ \begin{align*} \mathfrak{H}_{\mathcal{S}_0}(\mathrm{Fix}_G(\mathcal{T}))&=\{\mathrm{Fix}_G(\mathcal{R})/\mathrm{Fix}_G(\mathcal{T})\mid \mathcal{R}\in \mathfrak{T}_0, \mathcal{R}\subsetneq \mathcal{T} \\ &\qquad\,\mbox{and } \mathcal{R}\mbox{ is maximal for this property}\}. \end{align*} $$
Now, let
![]() $\{\mathcal {T}_1,\ldots , \mathcal {T}_s\}$
be the set of maximal complete proper subtrees of
$\{\mathcal {T}_1,\ldots , \mathcal {T}_s\}$
be the set of maximal complete proper subtrees of
![]() $\mathcal {T}$
. These can all be obtained from
$\mathcal {T}$
. These can all be obtained from
![]() $\mathcal {T}$
by removing the leaves adjacent to v, where v is a vertex of
$\mathcal {T}$
by removing the leaves adjacent to v, where v is a vertex of
![]() $\mathcal {T}$
that is not a leaf but such that all but one of its neighbours are leaves of
$\mathcal {T}$
that is not a leaf but such that all but one of its neighbours are leaves of
![]() $\mathcal {T}$
. Clearly,
$\mathcal {T}$
. Clearly,
![]() $\mathcal {T}_i\cup \mathcal {T}_j=\mathcal {T}$
for every
$\mathcal {T}_i\cup \mathcal {T}_j=\mathcal {T}$
for every
![]() $i\not =j$
and
$i\not =j$
and
![]() $\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
acts by permutation on the set
$\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
acts by permutation on the set
![]() $\{\mathcal {T}_1,\mathcal {T}_2,\ldots ,\mathcal {T}_s\}$
. Furthermore, for each
$\{\mathcal {T}_1,\mathcal {T}_2,\ldots ,\mathcal {T}_s\}$
. Furthermore, for each
![]() $i\in \{ 1,\ldots ,s\}$
, notice from Lemma 4.6 that
$i\in \{ 1,\ldots ,s\}$
, notice from Lemma 4.6 that
Furthermore, since
![]() $\mathcal {T}$
belongs to
$\mathcal {T}$
belongs to
![]() $\mathfrak {T}_0$
and contains at least a ball of radius
$\mathfrak {T}_0$
and contains at least a ball of radius
![]() $1$
around an edge, notice that
$1$
around an edge, notice that
![]() $\mathrm {Fix}_G(\mathcal {T}_i)\subseteq \operatorname {\mathrm {Stab}}_G(\mathcal {T})$
. However, this inclusion must be strict since
$\mathrm {Fix}_G(\mathcal {T}_i)\subseteq \operatorname {\mathrm {Stab}}_G(\mathcal {T})$
. However, this inclusion must be strict since
![]() $\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
contains either the fixator of a vertex of
$\operatorname {\mathrm {Stab}}_G(\mathcal {T})$
contains either the fixator of a vertex of
![]() $\mathcal {T}_i$
or the fixator of one of its edges. Now, Proposition 4.14 ensures the existence of an irreducible representation of
$\mathcal {T}_i$
or the fixator of one of its edges. Now, Proposition 4.14 ensures the existence of an irreducible representation of
![]() $\operatorname {\mathrm {Stab}}_G(\mathcal {T})/\mathrm {Fix}_G(\mathcal {T})$
without a nonzero
$\operatorname {\mathrm {Stab}}_G(\mathcal {T})/\mathrm {Fix}_G(\mathcal {T})$
without a nonzero
![]() $\mathrm {Fix}_G(\mathcal {T}_i)/\mathrm {Fix}_G(\mathcal {T})$
-invariant vector for every
$\mathrm {Fix}_G(\mathcal {T}_i)/\mathrm {Fix}_G(\mathcal {T})$
-invariant vector for every
![]() $i=1,\ldots ,s$
. Since every proper subtree
$i=1,\ldots ,s$
. Since every proper subtree
![]() $\mathcal {R}\in \mathfrak {T}_0$
of
$\mathcal {R}\in \mathfrak {T}_0$
of
![]() $\mathcal {T}$
is contained in one of these
$\mathcal {T}$
is contained in one of these
![]() $\mathcal {T}_i$
, this representation is an
$\mathcal {T}_i$
, this representation is an
![]() $\mathcal {S}_0$
-standard representation of
$\mathcal {S}_0$
-standard representation of
![]() $\operatorname {\mathrm {Stab}}_G(\mathcal {T})/\mathrm {Fix}_G(\mathcal {T})$
.
$\operatorname {\mathrm {Stab}}_G(\mathcal {T})/\mathrm {Fix}_G(\mathcal {T})$
.
The next lemma treats the remaining case
![]() $l=1$
where Proposition 4.14 does not apply.
$l=1$
where Proposition 4.14 does not apply.
Lemma 4.16. Let
![]() $G=G^+_{(i)}(Y_0,Y_1)$
and let
$G=G^+_{(i)}(Y_0,Y_1)$
and let
![]() $C\in \mathcal {F}_{\mathcal {S}_0}$
be a conjugacy class at height
$C\in \mathcal {F}_{\mathcal {S}_0}$
be a conjugacy class at height
![]() $1$
. Then, there exists an
$1$
. Then, there exists an
![]() $\mathcal {S}_{0}$
-standard representation of
$\mathcal {S}_{0}$
-standard representation of
![]() $\operatorname {\mathrm {Aut}}_{G}(C)$
.
$\operatorname {\mathrm {Aut}}_{G}(C)$
.
Proof. Lemma 4.5 ensures the existence of a vertex
![]() $v\in V(T)$
such that
$v\in V(T)$
such that
![]() ${C=\mathcal {C}(\mathrm {Fix}_{G}(B_T(v,1)))}$
. Let
${C=\mathcal {C}(\mathrm {Fix}_{G}(B_T(v,1)))}$
. Let
![]() $\mathcal {T}=B_T(v,r)$
. We recall as observed in Section 4.4 that
$\mathcal {T}=B_T(v,r)$
. We recall as observed in Section 4.4 that
![]() $\operatorname {\mathrm {Aut}}_G(C)\cong \operatorname {\mathrm {Stab}}_G(\mathcal {T})/\mathrm {Fix}_G(\mathcal {T})$
, where
$\operatorname {\mathrm {Aut}}_G(C)\cong \operatorname {\mathrm {Stab}}_G(\mathcal {T})/\mathrm {Fix}_G(\mathcal {T})$
, where
In particular,
![]() $\operatorname {\mathrm {Aut}}_G(C)$
can be realised as a the group of automorphisms of
$\operatorname {\mathrm {Aut}}_G(C)$
can be realised as a the group of automorphisms of
![]() $B_T(v,1)$
obtained by restricting the action of
$B_T(v,1)$
obtained by restricting the action of
![]() $\mathrm {Fix}_G(v)$
. Furthermore,
$\mathrm {Fix}_G(v)$
. Furthermore,
 $$ \begin{align*} \mathfrak{H}_{\mathcal{S}_0}(\mathrm{Fix}_G(\mathcal{T}))&=\{\mathrm{Fix}_G(\mathcal{R})/\mathrm{Fix}_G(\mathcal{T})\mid \mathcal{R}\in \mathfrak{T}_0, \mathcal{R}\subsetneq \mathcal{T} \\ &\qquad\,\mbox{and } \mathcal{R}\mbox{ is maximal for this property}\}\\ &=\{\mathrm{Fix}_G(f)/\mathrm{Fix}_G(B_T(v,1))\mid f\in E(B_T(v,1))\}. \end{align*} $$
$$ \begin{align*} \mathfrak{H}_{\mathcal{S}_0}(\mathrm{Fix}_G(\mathcal{T}))&=\{\mathrm{Fix}_G(\mathcal{R})/\mathrm{Fix}_G(\mathcal{T})\mid \mathcal{R}\in \mathfrak{T}_0, \mathcal{R}\subsetneq \mathcal{T} \\ &\qquad\,\mbox{and } \mathcal{R}\mbox{ is maximal for this property}\}\\ &=\{\mathrm{Fix}_G(f)/\mathrm{Fix}_G(B_T(v,1))\mid f\in E(B_T(v,1))\}. \end{align*} $$
Let d be the degree of v in T, let
![]() $X=E(B_T(v,1))$
and let
$X=E(B_T(v,1))$
and let
![]() $e\in X$
. Since
$e\in X$
. Since
![]() $\operatorname {\mathrm {Alt}}(d)\leq \underline {G}(v)$
and since
$\operatorname {\mathrm {Alt}}(d)\leq \underline {G}(v)$
and since
![]() $d\geq 4$
, notice that
$d\geq 4$
, notice that
![]() $\underline {G}(v)$
is
$\underline {G}(v)$
is
![]() $2$
-transitive. In particular,
$2$
-transitive. In particular,
![]() $\operatorname {\mathrm {Aut}}_{G}(C)$
is
$\operatorname {\mathrm {Aut}}_{G}(C)$
is
![]() $2$
-transitive on X and [Reference SemalSem23, Lemma 2.27] ensures the existence of an irreducible representation
$2$
-transitive on X and [Reference SemalSem23, Lemma 2.27] ensures the existence of an irreducible representation
![]() $\sigma $
of
$\sigma $
of
![]() $\operatorname {\mathrm {Aut}}_{G}(C)$
without a nonzero
$\operatorname {\mathrm {Aut}}_{G}(C)$
without a nonzero
![]() $\mathrm {Fix}_{\operatorname {\mathrm {Aut}}_{G}(C)}(e)$
-invariant vector. Since
$\mathrm {Fix}_{\operatorname {\mathrm {Aut}}_{G}(C)}(e)$
-invariant vector. Since
![]() $\mathrm {Fix}_G(v)$
is transitive on
$\mathrm {Fix}_G(v)$
is transitive on
![]() $E(B_T(v,1))$
, this representation does not admit a nonzero
$E(B_T(v,1))$
, this representation does not admit a nonzero
![]() $\mathrm {Fix}_{\operatorname {\mathrm {Aut}}_{G}(C)}(f)$
-invariant vector for any
$\mathrm {Fix}_{\operatorname {\mathrm {Aut}}_{G}(C)}(f)$
-invariant vector for any
![]() $f\in E(B_T(v,1))$
. The lemma follows from the fact that
$f\in E(B_T(v,1))$
. The lemma follows from the fact that
![]() $\mathrm { Fix}_{\operatorname {\mathrm {Aut}}_{G}(C)}(f)=\mathrm {Fix}_G(f)/\mathrm {Fix}_G(B_T(v,1))$
.
$\mathrm { Fix}_{\operatorname {\mathrm {Aut}}_{G}(C)}(f)=\mathrm {Fix}_G(f)/\mathrm {Fix}_G(B_T(v,1))$
.
5 Simple Radu groups are CCR
Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 4$
. Let i be a legal colouring of T and let
$d_0,d_1\geq 4$
. Let i be a legal colouring of T and let
![]() $Y_0,Y_1\subseteq \mathbb N$
be two finite subsets. The purpose of this section is to exploit the classification of the irreducible representations of
$Y_0,Y_1\subseteq \mathbb N$
be two finite subsets. The purpose of this section is to exploit the classification of the irreducible representations of
![]() $G^+_{(i)}(Y_0,Y_1)$
obtained from Sections 2 and 4.4 to prove that
$G^+_{(i)}(Y_0,Y_1)$
obtained from Sections 2 and 4.4 to prove that
![]() $G^+_{(i)}(Y_0,Y_1)$
is uniformly admissible and hence CCR.
$G^+_{(i)}(Y_0,Y_1)$
is uniformly admissible and hence CCR.
We recall that a totally disconnected locally compact group G is uniformly admissible if for every compact open subgroup K, there exists a positive integer
![]() $k_K$
such that
$k_K$
such that
![]() $\dim (\mathcal {H}_{\pi }^K)<k_K$
for every irreducible representation
$\dim (\mathcal {H}_{\pi }^K)<k_K$
for every irreducible representation
![]() $\pi $
of G. In particular, uniformly admissible groups are CCR. The following classical result ensures that the spherical representations of any Radu group are uniformly admissible.
$\pi $
of G. In particular, uniformly admissible groups are CCR. The following classical result ensures that the spherical representations of any Radu group are uniformly admissible.
Theorem 5.1. Let T be a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 3$
, let
$d_0,d_1\geq 3$
, let
![]() $G\leq \operatorname {\mathrm {Aut}}(T)$
be a closed noncompact subgroup acting transitively on the boundary of T and let
$G\leq \operatorname {\mathrm {Aut}}(T)$
be a closed noncompact subgroup acting transitively on the boundary of T and let
![]() $v\in V(T)$
. Then, for every integer
$v\in V(T)$
. Then, for every integer
![]() $n\geq 1$
, there exists a constant
$n\geq 1$
, there exists a constant
![]() $k_n\in \mathbb N$
such that
$k_n\in \mathbb N$
such that
![]() $\mathrm {dim}(\mathcal {H}_{\pi }^{K_n})<k_n$
for every spherical representation
$\mathrm {dim}(\mathcal {H}_{\pi }^{K_n})<k_n$
for every spherical representation
![]() $\pi $
of G admitting a nonzero
$\pi $
of G admitting a nonzero
![]() $\mathrm {Fix}_G(v)$
-invariant vector and where
$\mathrm {Fix}_G(v)$
-invariant vector and where
![]() $K_n=\mathrm { Fix}_G(B_T(v,n))$
.
$K_n=\mathrm { Fix}_G(B_T(v,n))$
.
Proof. Let
![]() $K=\mathrm {Fix}_G(v)$
and let
$K=\mathrm {Fix}_G(v)$
and let
![]() $\mu $
be the Haar measure of G renormalised in such a way that
$\mu $
be the Haar measure of G renormalised in such a way that
![]() $\mu (K)=1$
. Theorems 2.2 and 2.3 ensure that
$\mu (K)=1$
. Theorems 2.2 and 2.3 ensure that
![]() $(G,K)$
is a Gelfand pair and we observe that
$(G,K)$
is a Gelfand pair and we observe that
![]() $\mathrm {dim}(\mathcal {H}_{\pi }^K)= 1.$
Now let
$\mathrm {dim}(\mathcal {H}_{\pi }^K)= 1.$
Now let
![]() $\xi $
be a unit vector of
$\xi $
be a unit vector of
![]() $\mathcal {H}_{\pi }^K$
and let
$\mathcal {H}_{\pi }^K$
and let
![]() $\eta $
be a unit vector of
$\eta $
be a unit vector of
![]() $\mathcal {H}_{\pi }^{K_n}.$
Notice that
$\mathcal {H}_{\pi }^{K_n}.$
Notice that
is a K-right invariant and
![]() $K_n$
-left invariant continuous function. However, since
$K_n$
-left invariant continuous function. However, since
![]() $\mathrm {dim}(\mathcal {H}_{\pi }^K)= 1$
, notice for all
$\mathrm {dim}(\mathcal {H}_{\pi }^K)= 1$
, notice for all
![]() $g,h\in G$
that
$g,h\in G$
that
 $$ \begin{align*} \int_K\varphi_{\xi,\eta}(gkh)\,\mathrm{d}\mu(k)&=\bigg\langle \int_K \pi(gkh)\xi,\eta\bigg\rangle\\ &=\bigg\langle \pi(h)\xi,\int_K\pi(k^{-1})\pi(g^{-1})\eta\bigg\rangle\\ &=\langle \pi(h)\xi,\alpha(\eta, g)\xi\rangle=\overline{\alpha(\eta, g)}\varphi_{\xi,\xi}(h) \end{align*} $$
$$ \begin{align*} \int_K\varphi_{\xi,\eta}(gkh)\,\mathrm{d}\mu(k)&=\bigg\langle \int_K \pi(gkh)\xi,\eta\bigg\rangle\\ &=\bigg\langle \pi(h)\xi,\int_K\pi(k^{-1})\pi(g^{-1})\eta\bigg\rangle\\ &=\langle \pi(h)\xi,\alpha(\eta, g)\xi\rangle=\overline{\alpha(\eta, g)}\varphi_{\xi,\xi}(h) \end{align*} $$
for some
![]() $\alpha (\eta , g)\in \mathbb C$
. However,
$\alpha (\eta , g)\in \mathbb C$
. However,
![]() $\varphi _{\xi ,\xi }(1_G)=1$
and hence
$\varphi _{\xi ,\xi }(1_G)=1$
and hence
![]() $\overline {\alpha (\eta , g)}=\varphi _{\xi ,\eta }(g)$
. This implies for all
$\overline {\alpha (\eta , g)}=\varphi _{\xi ,\eta }(g)$
. This implies for all
![]() $g,h\in G$
that
$g,h\in G$
that
Since
![]() $\varphi _{\xi ,\eta }$
is K-right invariant and
$\varphi _{\xi ,\eta }$
is K-right invariant and
![]() $K_n$
-left invariant, notice that it can be realised as a function
$K_n$
-left invariant, notice that it can be realised as a function
![]() $\phi :Gv\rightarrow \mathbb C$
on the orbit
$\phi :Gv\rightarrow \mathbb C$
on the orbit
![]() $Gv$
of v in
$Gv$
of v in
![]() $V(T)$
that is constant on the
$V(T)$
that is constant on the
![]() $K_n$
-orbits of v. However, since
$K_n$
-orbits of v. However, since
![]() $K_n$
is an open subgroup of the compact group K, the index of
$K_n$
is an open subgroup of the compact group K, the index of
![]() $K_n$
in K is finite. Since K is transitive on the boundary of the tree, this implies that
$K_n$
in K is finite. Since K is transitive on the boundary of the tree, this implies that
![]() $K_n$
has finitely many orbits on
$K_n$
has finitely many orbits on
![]() $\partial T$
. In particular, there exists an integer
$\partial T$
. In particular, there exists an integer
![]() $N_n\geq \max \{2,n\}$
such that
$N_n\geq \max \{2,n\}$
such that
![]() $\partial T(w,v)$
is contained in a single
$\partial T(w,v)$
is contained in a single
![]() $K_n$
-orbit for all
$K_n$
-orbit for all
![]() $w\in \partial B_T(v,N_n)$
, where
$w\in \partial B_T(v,N_n)$
, where
![]() $\partial T(w,v)$
is the set of ends of
$\partial T(w,v)$
is the set of ends of
![]() $T(w,v)=\{u\in V(T)\mid d_T(u,w)<d_T(u,v)\}$
that are not vertices. Now notice that the value of
$T(w,v)=\{u\in V(T)\mid d_T(u,w)<d_T(u,v)\}$
that are not vertices. Now notice that the value of
![]() $\phi $
on every vertex
$\phi $
on every vertex
![]() $w\in Gv$
can be computed iteratively from the values that
$w\in Gv$
can be computed iteratively from the values that
![]() $\phi $
takes on vertices of
$\phi $
takes on vertices of
![]() $B_T(v,N_n)$
. More precisely, let w be any vertex in
$B_T(v,N_n)$
. More precisely, let w be any vertex in
![]() $Gv - B_T(v,N_n)$
and let u be the vertex of
$Gv - B_T(v,N_n)$
and let u be the vertex of
![]() $Gv$
at distance
$Gv$
at distance
![]() $2$
from w that is closer to
$2$
from w that is closer to
![]() $B_T(v,N_n)$
than any other vertex of
$B_T(v,N_n)$
than any other vertex of
![]() $Gv$
at distance
$Gv$
at distance
![]() $2$
from w. Let
$2$
from w. Let
![]() $t\in G$
be such that
$t\in G$
be such that
![]() $d_T(v,t v)=2$
,
$d_T(v,t v)=2$
,
![]() $g\in G$
be such that
$g\in G$
be such that
![]() $gv=u$
and note from Equation (5-1) (taking
$gv=u$
and note from Equation (5-1) (taking
![]() $h = t$
) that
$h = t$
) that
Now note that every vertex in
![]() $\{gkt v : k \in K\}$
is either in the same
$\{gkt v : k \in K\}$
is either in the same
![]() $K_n$
-orbit as w or is strictly closer to
$K_n$
-orbit as w or is strictly closer to
![]() $B_T(v,N_n)$
than w. In particular, Equation (5-2) expresses
$B_T(v,N_n)$
than w. In particular, Equation (5-2) expresses
![]() $\phi (w)$
as a linear combination of the values that
$\phi (w)$
as a linear combination of the values that
![]() $\phi $
takes on vertices that are strictly closer to
$\phi $
takes on vertices that are strictly closer to
![]() $B_T(v,N_n)$
than w. Now, for each of these vertices that do not already belong to
$B_T(v,N_n)$
than w. Now, for each of these vertices that do not already belong to
![]() $B_T(v,N_n)$
, we can apply the same reasoning and obtain the value that
$B_T(v,N_n)$
, we can apply the same reasoning and obtain the value that
![]() $\phi $
takes on it in terms of the values that
$\phi $
takes on it in terms of the values that
![]() $\phi $
takes on vertices that are even closer to
$\phi $
takes on vertices that are even closer to
![]() $B_T(v,N_n)$
. Since
$B_T(v,N_n)$
. Since
![]() $N_n$
has been chosen to be at least
$N_n$
has been chosen to be at least
![]() $2$
, this process must end at some point and one obtains an expression for
$2$
, this process must end at some point and one obtains an expression for
![]() $\phi (w)$
as a linear combination of the values that
$\phi (w)$
as a linear combination of the values that
![]() $\phi $
takes on the vertices of
$\phi $
takes on the vertices of
![]() $B_T(v,N_n)$
. This implies that the space
$B_T(v,N_n)$
. This implies that the space
![]() $\mathcal {L}_n$
of functions
$\mathcal {L}_n$
of functions
![]() $\varphi :G\rightarrow \mathbb C$
that are K-right invariant,
$\varphi :G\rightarrow \mathbb C$
that are K-right invariant,
![]() $K_n$
-left invariant and satisfy Equation (5-1) has finite dimension bounded by the cardinality
$K_n$
-left invariant and satisfy Equation (5-1) has finite dimension bounded by the cardinality
![]() $k_n$
of
$k_n$
of
![]() $B_T(v,N_n)$
. Furthermore, since
$B_T(v,N_n)$
. Furthermore, since
![]() $\pi $
is irreducible, notice that
$\pi $
is irreducible, notice that
![]() $\xi $
is cyclic and therefore that the linear map
$\xi $
is cyclic and therefore that the linear map
![]() $\Psi _n: \mathcal {H}_{\pi }^{K_n}\rightarrow \mathcal {L}_n: \eta \rightarrow \overline {\varphi _{\xi ,\eta }}$
is injective. This proves as desired that
$\Psi _n: \mathcal {H}_{\pi }^{K_n}\rightarrow \mathcal {L}_n: \eta \rightarrow \overline {\varphi _{\xi ,\eta }}$
is injective. This proves as desired that
![]() $\dim (\mathcal {H}_{\pi }^{K_n})\leq \dim (\mathcal {L}_n)\leq k_n<+\infty $
.
$\dim (\mathcal {H}_{\pi }^{K_n})\leq \dim (\mathcal {L}_n)\leq k_n<+\infty $
.
In addition, the following classical result provides a bound for every special and cuspidal representation.
Theorem 5.2 [HC70, Corollary of Theorem 2].
Let G be a locally compact group,
![]() $\pi $
be an irreducible square-integrable representation of G and
$\pi $
be an irreducible square-integrable representation of G and
![]() $K\leq G$
be a compact open subgroup. Then, there exists a positive integer
$K\leq G$
be a compact open subgroup. Then, there exists a positive integer
![]() $k_{K,\pi }$
depending on K and
$k_{K,\pi }$
depending on K and
![]() $\pi $
such that
$\pi $
such that
![]() $\dim (\mathcal {H}_{\pi }^K)\leq k_{K,\pi }$
.
$\dim (\mathcal {H}_{\pi }^K)\leq k_{K,\pi }$
.
Putting it all together, we can prove the result announced at the beginning of the section.
Theorem 5.3.
![]() $G^+_{(i)}(Y_0,Y_1)$
is uniformly admissible, and hence CCR.
$G^+_{(i)}(Y_0,Y_1)$
is uniformly admissible, and hence CCR.
Proof. Let
![]() $G=G^+_{(i)}(Y_0,Y_1)$
. Let
$G=G^+_{(i)}(Y_0,Y_1)$
. Let
![]() $K\leq G$
be a compact open subgroup, and let
$K\leq G$
be a compact open subgroup, and let
![]() $v\in V$
. For each
$v\in V$
. For each
![]() $n\in \mathbb N$
, let
$n\in \mathbb N$
, let
![]() $K_n=\mathrm {Fix}_G(B_T(v,n))$
and notice that Theorem 5.1 ensures the existence of a positive integer
$K_n=\mathrm {Fix}_G(B_T(v,n))$
and notice that Theorem 5.1 ensures the existence of a positive integer
![]() $k_{n}$
such that
$k_{n}$
such that
![]() $\dim (\mathcal {H}_{\pi }^{K_n})\leq k_{n}$
for every spherical representation
$\dim (\mathcal {H}_{\pi }^{K_n})\leq k_{n}$
for every spherical representation
![]() $\pi $
of G. Now, for every
$\pi $
of G. Now, for every
![]() $n\in \mathbb N$
, we let
$n\in \mathbb N$
, we let
![]() $\Sigma _n$
be the subset of all equivalence classes of nonspherical irreducible representations of G admitting nonzero
$\Sigma _n$
be the subset of all equivalence classes of nonspherical irreducible representations of G admitting nonzero
![]() $K_n$
-invariant vectors. The classification of special and cuspidal representations of G provided by Theorems 2.5 and 4.12 ensures that
$K_n$
-invariant vectors. The classification of special and cuspidal representations of G provided by Theorems 2.5 and 4.12 ensures that
![]() $\Sigma _n$
is finite. Furthermore, for every
$\Sigma _n$
is finite. Furthermore, for every
![]() $\sigma \in \Sigma _n$
, Theorem 5.2 provides a constant
$\sigma \in \Sigma _n$
, Theorem 5.2 provides a constant
![]() $k_{\sigma , n}$
such that
$k_{\sigma , n}$
such that
![]() $\dim (\mathcal {H}_{\pi }^{K_n})\leq k_{\sigma , n}$
. In particular, for each
$\dim (\mathcal {H}_{\pi }^{K_n})\leq k_{\sigma , n}$
. In particular, for each
![]() $n\in \mathbb N$
, the constant
$n\in \mathbb N$
, the constant
![]() $k^{\prime }_n=\max _{\sigma \in \Sigma _n} k_{\sigma , n}$
is finite and
$k^{\prime }_n=\max _{\sigma \in \Sigma _n} k_{\sigma , n}$
is finite and
![]() $\dim (\mathcal {H}_{\pi }^{K_n})< k^{\prime }_n$
for each special and cuspidal representation
$\dim (\mathcal {H}_{\pi }^{K_n})< k^{\prime }_n$
for each special and cuspidal representation
![]() $\pi $
of G. It follows that
$\pi $
of G. It follows that
![]() $\dim (\mathcal {H}_{\pi }^{K_n})\leq \max \{k_{n}, k^{\prime }_{n}\}$
for all
$\dim (\mathcal {H}_{\pi }^{K_n})\leq \max \{k_{n}, k^{\prime }_{n}\}$
for all
![]() $\pi \in \widehat {G}$
and every
$\pi \in \widehat {G}$
and every
![]() $n\in \mathbb N$
. However, since
$n\in \mathbb N$
. However, since
![]() $(K_n)_{n\in \mathbb N}$
is a basis of neighbourhoods of the identity, there exists some
$(K_n)_{n\in \mathbb N}$
is a basis of neighbourhoods of the identity, there exists some
![]() $N\in \mathbb N$
such that
$N\in \mathbb N$
such that
![]() $K_N\subseteq K$
. It follows that
$K_N\subseteq K$
. It follows that
Appendix Irreducible representations of a group and subgroups of index
 $2$
$2$
The purpose of this appendix is to explain the relations between the irreducible unitary representations of a locally compact group G and the irreducible representations of its closed subgroups
![]() $H\leq G$
of index
$H\leq G$
of index
![]() $2$
. Among other things, Theorem A.2 below explains the correspondence between these representations. Furthermore, when G is a totally disconnected locally compact group, we show that G is uniformly admissible if and only if H is uniformly admissible; see Lemma A.9.
$2$
. Among other things, Theorem A.2 below explains the correspondence between these representations. Furthermore, when G is a totally disconnected locally compact group, we show that G is uniformly admissible if and only if H is uniformly admissible; see Lemma A.9.
The relevance of this appendix is given by Theorem 3.5, which ensures that every Radu group G belongs to a finite chain
![]() $H_n\geq \cdots \geq H_0$
with
$H_n\geq \cdots \geq H_0$
with
![]() $n\in \{0,1,2,3\}$
such that
$n\in \{0,1,2,3\}$
such that
![]() $H_n=G$
,
$H_n=G$
,
![]() $\lbrack H_t: H_{t-1} \rbrack =2$
for all t and where
$\lbrack H_t: H_{t-1} \rbrack =2$
for all t and where
![]() $H_0$
is conjugate in
$H_0$
is conjugate in
![]() $\operatorname {\mathrm {Aut}}(T)^+$
to
$\operatorname {\mathrm {Aut}}(T)^+$
to
![]() $G_{(i)}^+(Y_0,Y_1)$
if T is a
$G_{(i)}^+(Y_0,Y_1)$
if T is a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 6$
. As a direct consequence, we therefore obtain a description of the irreducible representations of these groups and observe that they are uniformly admissible. More precisely, the spherical and special representations of any Radu group G are classified by Section 2 and a description of the cuspidal representations of these groups can be obtained from the description of cuspidal representations of
$d_0,d_1\geq 6$
. As a direct consequence, we therefore obtain a description of the irreducible representations of these groups and observe that they are uniformly admissible. More precisely, the spherical and special representations of any Radu group G are classified by Section 2 and a description of the cuspidal representations of these groups can be obtained from the description of cuspidal representations of
![]() $G_{(i)}^+(Y_0,Y_1)$
given in Section 4 by applying Theorem A.2 several times.
$G_{(i)}^+(Y_0,Y_1)$
given in Section 4 by applying Theorem A.2 several times.
A.1 Preliminaries
Let G be a locally compact group and let
![]() $H\leq G$
be a closed normal subgroup of finite index (in particular, H is open in G). The purpose of this section is to recall three operations that can be applied either to the representations of G or to those of H.
$H\leq G$
be a closed normal subgroup of finite index (in particular, H is open in G). The purpose of this section is to recall three operations that can be applied either to the representations of G or to those of H.
We start with the conjugation of representations. For every
![]() $g\in G$
, we denote by
$g\in G$
, we denote by
the conjugation map and for every representation
![]() $\pi $
of H, we define the morphism
$\pi $
of H, we define the morphism
![]() $\pi ^g= \pi \circ c(g)$
. Since H is normal in G, notice that
$\pi ^g= \pi \circ c(g)$
. Since H is normal in G, notice that
![]() $\pi ^g$
is a well-defined representation of H on the Hilbert space
$\pi ^g$
is a well-defined representation of H on the Hilbert space
![]() $\mathcal {H}_{\pi }$
. This representation is called the conjugate representation of
$\mathcal {H}_{\pi }$
. This representation is called the conjugate representation of
![]() $\pi $
by g. Furthermore, notice that the conjugate representation
$\pi $
by g. Furthermore, notice that the conjugate representation
![]() $\pi ^g$
depends up to equivalence only on the coset
$\pi ^g$
depends up to equivalence only on the coset
![]() $gH$
and that
$gH$
and that
![]() $\pi ^g$
is irreducible if and only if
$\pi ^g$
is irreducible if and only if
![]() $\pi $
is irreducible. In particular, the action by conjugation of G on
$\pi $
is irreducible. In particular, the action by conjugation of G on
![]() $\widehat {H}$
passes to the quotient
$\widehat {H}$
passes to the quotient
![]() $G/H$
.
$G/H$
.
Now, let
![]() $G'$
be another topological group, let
$G'$
be another topological group, let
![]() $\phi :G \rightarrow G'$
be a continuous group homomorphism, let
$\phi :G \rightarrow G'$
be a continuous group homomorphism, let
![]() $\pi $
be a representation of G and let
$\pi $
be a representation of G and let ![]() be a unitary character of
be a unitary character of
![]() $G'$
. We define the twisted representation
$G'$
. We define the twisted representation
![]() $\pi ^\chi $
as the representation of G on
$\pi ^\chi $
as the representation of G on
![]() $\mathcal {H}_{\pi }$
given by
$\mathcal {H}_{\pi }$
given by
Notice that this representation is still continuous and unitary since ![]() and
and
![]() $\phi $
are continuous group homomorphisms, and since
$\phi $
are continuous group homomorphisms, and since ![]() and
and
![]() $\pi $
are unitary. Note also that
$\pi $
are unitary. Note also that
![]() $\pi ^\chi \cong \pi $
if
$\pi ^\chi \cong \pi $
if ![]() is the trivial representation of
is the trivial representation of
![]() $G'$
.
$G'$
.
Lemma A.1.
![]() $\pi ^\chi $
is irreducible if and only if
$\pi ^\chi $
is irreducible if and only if
![]() $\pi $
is irreducible.
$\pi $
is irreducible.
Proof. Since ![]() is a unitary complex number for every
is a unitary complex number for every
![]() $g\in G$
, notice that, for every
$g\in G$
, notice that, for every
![]() $\xi \in \mathcal {H}_{\pi }$
, the subspace of
$\xi \in \mathcal {H}_{\pi }$
, the subspace of
![]() $\mathcal {H}_{\pi }$
spanned by
$\mathcal {H}_{\pi }$
spanned by
![]() $\{\pi (g)\xi \mid g\in G\}$
is the same as the subspace spanned by
$\{\pi (g)\xi \mid g\in G\}$
is the same as the subspace spanned by ![]() . The result therefore follows from the fact that a representation is irreducible if and only if every nonzero vector is cyclic.
. The result therefore follows from the fact that a representation is irreducible if and only if every nonzero vector is cyclic.
Finally, we recall the notion of induction. Since most of the complexity vanishes when H is an open subgroup of G (because the quotient space
![]() $G/H$
is discrete) and since this is the only setup encountered in these notes, we work under this hypothesis. We refer to [Reference Kaniuth and TaylorKT13, Chs.
$G/H$
is discrete) and since this is the only setup encountered in these notes, we work under this hypothesis. We refer to [Reference Kaniuth and TaylorKT13, Chs.
![]() $2.1$
and
$2.1$
and
![]() $2.2$
] for details. Let G be a locally compact group, let
$2.2$
] for details. Let G be a locally compact group, let
![]() $H\leq G$
be an open subgroup and let
$H\leq G$
be an open subgroup and let
![]() $\sigma $
be a representation of H. The induced representation
$\sigma $
be a representation of H. The induced representation
![]() $\operatorname {\mathrm {Ind}}_{H}^G(\sigma )$
is a representation of G with representation space given by
$\operatorname {\mathrm {Ind}}_{H}^G(\sigma )$
is a representation of G with representation space given by
 $$ \begin{align*}\operatorname{\mathrm{Ind}}_H^G(\mathcal{H}_{\sigma})=\bigg\{\phi:G\rightarrow\mathcal{H}_{\sigma}\,\bigg|\, \phi(gh)=\sigma(h^{-1})\phi(g), \sum\limits_{gH\in G/H}^{}\langle \phi(g),\phi(g)\rangle<+\infty \bigg\}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Ind}}_H^G(\mathcal{H}_{\sigma})=\bigg\{\phi:G\rightarrow\mathcal{H}_{\sigma}\,\bigg|\, \phi(gh)=\sigma(h^{-1})\phi(g), \sum\limits_{gH\in G/H}^{}\langle \phi(g),\phi(g)\rangle<+\infty \bigg\}.\end{align*} $$
For
![]() $\psi , \phi \in \operatorname {\mathrm {Ind}}_H^G(\mathcal {H}_{\sigma })$
,
$\psi , \phi \in \operatorname {\mathrm {Ind}}_H^G(\mathcal {H}_{\sigma })$
,
 $$ \begin{align*} \langle \psi,\phi\rangle_{\operatorname{\mathrm{Ind}}_H^G(\mathcal{H}_{\sigma})}= \sum\limits_{gH\in G/H}^{} \langle \psi(g),\phi(g)\rangle. \end{align*} $$
$$ \begin{align*} \langle \psi,\phi\rangle_{\operatorname{\mathrm{Ind}}_H^G(\mathcal{H}_{\sigma})}= \sum\limits_{gH\in G/H}^{} \langle \psi(g),\phi(g)\rangle. \end{align*} $$
Equipped with this inner product,
![]() $\operatorname {\mathrm {Ind}}_H^G(\mathcal {H}_{\sigma })$
is a separable complex Hilbert space. The induced representation
$\operatorname {\mathrm {Ind}}_H^G(\mathcal {H}_{\sigma })$
is a separable complex Hilbert space. The induced representation
![]() $\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is the representation of G on
$\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is the representation of G on
![]() $\operatorname {\mathrm {Ind}}_H^G(\mathcal {H}_{\sigma })$
defined by
$\operatorname {\mathrm {Ind}}_H^G(\mathcal {H}_{\sigma })$
defined by
A.2 The explicit correspondence
We come back to the context in which we are interested. Let G be a locally compact group and let
![]() $H\leq G$
be a closed subgroup of index
$H\leq G$
be a closed subgroup of index
![]() $2$
in G. In particular, H is an normal open subgroup of G and the quotient
$2$
in G. In particular, H is an normal open subgroup of G and the quotient
![]() ${G'=G/H}$
is isomorphic to the cyclic group of order two. Let
${G'=G/H}$
is isomorphic to the cyclic group of order two. Let
![]() $\tau $
denote the only irreducible nontrivial representation of
$\tau $
denote the only irreducible nontrivial representation of
![]() $G/H$
. Let
$G/H$
. Let
![]() $t\in G-H$
, let
$t\in G-H$
, let
![]() $\phi : G \rightarrow G/H$
be the canonical projection on the quotient and, for every representation
$\phi : G \rightarrow G/H$
be the canonical projection on the quotient and, for every representation
![]() $\pi $
of G, let
$\pi $
of G, let
![]() $\pi ^\tau $
be the twisted representation of G as defined in Section A.1. The purpose of this section is to prove the following theorem.
$\pi ^\tau $
be the twisted representation of G as defined in Section A.1. The purpose of this section is to prove the following theorem.
Theorem A.2. For every irreducible representation
![]() $\pi $
of G:
$\pi $
of G:
-
•
 $\pi \not \cong \pi ^\tau $
if and only if
$\pi \not \cong \pi ^\tau $
if and only if
 $\operatorname {\mathrm {Res}}_H^G(\pi )$
is an irreducible representation of H and in that case,
$\operatorname {\mathrm {Res}}_H^G(\pi )$
is an irreducible representation of H and in that case,
 $\operatorname {\mathrm {Res}}_H^G(\pi )\cong \operatorname {\mathrm {Res}}_H^G(\pi )^t$
;
$\operatorname {\mathrm {Res}}_H^G(\pi )\cong \operatorname {\mathrm {Res}}_H^G(\pi )^t$
; -
•
 $\pi \cong \pi ^\tau $
if and only if
$\pi \cong \pi ^\tau $
if and only if
 $\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
for some irreducible representation
$\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
for some irreducible representation
 $\sigma $
of H and in that case,
$\sigma $
of H and in that case,
 $\sigma \not \cong \sigma ^t$
.
$\sigma \not \cong \sigma ^t$
.
For every irreducible representation
![]() $\sigma $
of H:
$\sigma $
of H:
-
•
 $\sigma \not \cong \sigma ^t$
if and only if
$\sigma \not \cong \sigma ^t$
if and only if
 $\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is an irreducible representation of G and in that case,
$\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is an irreducible representation of G and in that case,
 $\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \operatorname {\mathrm {Ind}}_H^G(\sigma )^\tau $
;
$\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \operatorname {\mathrm {Ind}}_H^G(\sigma )^\tau $
; -
•
 $\sigma \cong \sigma ^t$
if and only if
$\sigma \cong \sigma ^t$
if and only if
 $\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi ^\tau $
for some irreducible representation
$\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi ^\tau $
for some irreducible representation
 $\pi $
of G and in that case,
$\pi $
of G and in that case,
 $\pi \not \cong \pi ^\tau $
.
$\pi \not \cong \pi ^\tau $
.
Furthermore:
-
(1) every irreducible representation
 $\pi $
of G satisfies
$\pi $
of G satisfies
 $\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma )$
for some irreducible representation
$\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma )$
for some irreducible representation
 $\sigma $
of H;
$\sigma $
of H; -
(2) every irreducible representation
 $\sigma $
of H satisfies
$\sigma $
of H satisfies
 $\sigma \leq \operatorname {\mathrm {Res}}_H^G(\pi )$
for some irreducible representation
$\sigma \leq \operatorname {\mathrm {Res}}_H^G(\pi )$
for some irreducible representation
 $\pi $
of G.
$\pi $
of G.
The proof of this theorem is gathered in the following few results. First, let us recall the weak version of Frobenius reciprocity that we use several times throughout the proof.
Theorem A.3 [Reference MackeyMac76, Corollary
 $1$
of Theorem
$1$
of Theorem
 $3.8$
].
$3.8$
].
Let G be a locally compact group and let
![]() $H\leq G$
be a closed subgroup of G. Then, for every representation
$H\leq G$
be a closed subgroup of G. Then, for every representation
![]() $\pi $
of G and every representation
$\pi $
of G and every representation
![]() $\sigma $
of H,
$\sigma $
of H,
where
![]() $\mathrm {I}(\pi _1,\pi _2)$
is the dimension of the space of intertwining operators between the two representations
$\mathrm {I}(\pi _1,\pi _2)$
is the dimension of the space of intertwining operators between the two representations
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
. Furthermore, if the index of H in G is finite, this relation becomes an equality.
$\pi _2$
. Furthermore, if the index of H in G is finite, this relation becomes an equality.
Now, let us make a few observations.
Lemma A.4. Let
![]() $\sigma $
be an irreducible representation of H. Then,
$\sigma $
be an irreducible representation of H. Then,
Proof. Set
By definition of
![]() $\operatorname {\mathrm {Ind}}_H^G(\mathcal {H}_{\sigma })$
and since
$\operatorname {\mathrm {Ind}}_H^G(\mathcal {H}_{\sigma })$
and since
![]() $G= H\sqcup Ht$
, it is clear that
$G= H\sqcup Ht$
, it is clear that
Now, notice that
![]() $\mathcal {U}: \mathcal {L}\rightarrow \mathcal {H}_{\sigma }: \varphi \mapsto \varphi (1_G)$
is a unitary operator and that for every
$\mathcal {U}: \mathcal {L}\rightarrow \mathcal {H}_{\sigma }: \varphi \mapsto \varphi (1_G)$
is a unitary operator and that for every
![]() $h\in H$
and every
$h\in H$
and every
![]() $\varphi \in \mathcal {L}$
,
$\varphi \in \mathcal {L}$
,
In particular, this proves that
![]() $(\operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma )), \mathcal {L})\cong (\sigma ,\mathcal {H}_{\sigma })$
. Similarly, notice that
$(\operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma )), \mathcal {L})\cong (\sigma ,\mathcal {H}_{\sigma })$
. Similarly, notice that
![]() $\mathcal {U}^t: \mathcal {L}^t\rightarrow \mathcal {H}_{\sigma }: \varphi \mapsto \varphi (t^{-1})$
is a unitary operator and that for every
$\mathcal {U}^t: \mathcal {L}^t\rightarrow \mathcal {H}_{\sigma }: \varphi \mapsto \varphi (t^{-1})$
is a unitary operator and that for every
![]() $h\in H$
and every
$h\in H$
and every
![]() $\varphi \in \mathcal {L}^t$
,
$\varphi \in \mathcal {L}^t$
,
 $$ \begin{align*} \sigma^t(h)\mathcal{U}^t\varphi&=\sigma(tht^{-1})\varphi(t^{-1})=\varphi(t^{-1}th^{-1}t^{-1})\\ &=\varphi(h^{-1}t^{-1})=\lbrack \operatorname{\mathrm{Ind}}_H^G(\sigma)(h)\rbrack\varphi(t^{-1})=\mathcal{U}^t\lbrack \operatorname{\mathrm{Ind}}_H^G(\sigma)(h)\rbrack\varphi. \end{align*} $$
$$ \begin{align*} \sigma^t(h)\mathcal{U}^t\varphi&=\sigma(tht^{-1})\varphi(t^{-1})=\varphi(t^{-1}th^{-1}t^{-1})\\ &=\varphi(h^{-1}t^{-1})=\lbrack \operatorname{\mathrm{Ind}}_H^G(\sigma)(h)\rbrack\varphi(t^{-1})=\mathcal{U}^t\lbrack \operatorname{\mathrm{Ind}}_H^G(\sigma)(h)\rbrack\varphi. \end{align*} $$
This proves that
![]() $(\operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma )), \mathcal {L}^t)\cong (\sigma ^t,\mathcal {H}_{\sigma ^t})$
and we obtain as desired that
$(\operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma )), \mathcal {L}^t)\cong (\sigma ^t,\mathcal {H}_{\sigma ^t})$
and we obtain as desired that
![]() $\operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))\cong \sigma \oplus \sigma ^t$
.
$\operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))\cong \sigma \oplus \sigma ^t$
.
Lemma A.5. Let
![]() $\pi $
be an irreducible representation of G. Then exactly one of the following happens:
$\pi $
be an irreducible representation of G. Then exactly one of the following happens:
-
•
 $\operatorname {\mathrm {Res}}_H^G(\pi )$
is an irreducible representation of H and
$\operatorname {\mathrm {Res}}_H^G(\pi )$
is an irreducible representation of H and
 $\operatorname {\mathrm {Res}}_H^G(\pi )\cong \operatorname {\mathrm {Res}}_H^G(\pi )^t$
;
$\operatorname {\mathrm {Res}}_H^G(\pi )\cong \operatorname {\mathrm {Res}}_H^G(\pi )^t$
; -
•
 $\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
for some irreducible representation
$\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
for some irreducible representation
 $\sigma $
of H.
$\sigma $
of H.
Proof. If
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )$
is an irreducible representation of H, notice for every
$\operatorname {\mathrm {Res}}_H^G(\pi )$
is an irreducible representation of H, notice for every
![]() $h\in H$
and every
$h\in H$
and every
![]() $\xi \in \mathcal {H}_{\pi }$
that
$\xi \in \mathcal {H}_{\pi }$
that
 $$ \begin{align*} \pi(t)\lbrack \operatorname{\mathrm{Res}}_H^G(\pi)(h)\rbrack \xi&=\pi(t)\pi(h)\xi=\pi(tht^{-1})\pi(t)\xi\\ &=\lbrack \operatorname{\mathrm{Res}}_H^G(\pi)(tht^{-1})\rbrack\pi(t)\xi=\lbrack\operatorname{\mathrm{Res}}_H^G(\pi)^t(h)\rbrack\pi(t)\xi. \end{align*} $$
$$ \begin{align*} \pi(t)\lbrack \operatorname{\mathrm{Res}}_H^G(\pi)(h)\rbrack \xi&=\pi(t)\pi(h)\xi=\pi(tht^{-1})\pi(t)\xi\\ &=\lbrack \operatorname{\mathrm{Res}}_H^G(\pi)(tht^{-1})\rbrack\pi(t)\xi=\lbrack\operatorname{\mathrm{Res}}_H^G(\pi)^t(h)\rbrack\pi(t)\xi. \end{align*} $$
In particular,
![]() $\pi (t):\mathcal {H}_{\pi }\rightarrow \mathcal {H}_{\pi }$
is an intertwining operator between
$\pi (t):\mathcal {H}_{\pi }\rightarrow \mathcal {H}_{\pi }$
is an intertwining operator between
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )$
and
$\operatorname {\mathrm {Res}}_H^G(\pi )$
and
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )^t$
, which settles the first case.
$\operatorname {\mathrm {Res}}_H^G(\pi )^t$
, which settles the first case.
Now, suppose that
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )$
is not an irreducible representation of G. Since
$\operatorname {\mathrm {Res}}_H^G(\pi )$
is not an irreducible representation of G. Since
![]() $\pi $
is irreducible, any nonzero
$\pi $
is irreducible, any nonzero
![]() $\xi \in \mathcal {H}_{\pi }$
is a cyclic vector. Hence, the subspace spanned by
$\xi \in \mathcal {H}_{\pi }$
is a cyclic vector. Hence, the subspace spanned by
![]() $\{\pi (g)\xi \mid g\in G\}$
is dense in
$\{\pi (g)\xi \mid g\in G\}$
is dense in
![]() $\mathcal {H}_{\pi }$
. However, since
$\mathcal {H}_{\pi }$
. However, since
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )$
is not irreducible, there exists a nonzero vector
$\operatorname {\mathrm {Res}}_H^G(\pi )$
is not irreducible, there exists a nonzero vector
![]() $\xi \in \mathcal {H}_{\pi }$
such that the subspace spanned by
$\xi \in \mathcal {H}_{\pi }$
such that the subspace spanned by
![]() $\{\pi (h)\xi \mid h\in H\}$
is not dense in
$\{\pi (h)\xi \mid h\in H\}$
is not dense in
![]() $\mathcal {H}_{\pi }$
. Let M denote the closure of this space. First, let us show that
$\mathcal {H}_{\pi }$
. Let M denote the closure of this space. First, let us show that
![]() $(\operatorname {\mathrm {Res}}_H^G(\pi ),M)$
is irreducible. To do this, let N be a proper
$(\operatorname {\mathrm {Res}}_H^G(\pi ),M)$
is irreducible. To do this, let N be a proper
![]() $\pi (H)$
-invariant subspace of M and let us show that
$\pi (H)$
-invariant subspace of M and let us show that
![]() $N=\{0\}$
. To begin with, notice that for every closed
$N=\{0\}$
. To begin with, notice that for every closed
![]() $\pi (H)$
-invariant subspace L of
$\pi (H)$
-invariant subspace L of
![]() $\mathcal {H}_{\pi }$
, the subspace
$\mathcal {H}_{\pi }$
, the subspace
![]() $\pi (t)L$
is also
$\pi (t)L$
is also
![]() $\pi (H)$
-invariant since
$\pi (H)$
-invariant since
![]() $\pi (H)\pi (t)L=\pi (Ht)L=\pi (tH)L=\pi (t)L$
. Now, since
$\pi (H)\pi (t)L=\pi (Ht)L=\pi (tH)L=\pi (t)L$
. Now, since
![]() $\xi $
is a cyclic vector for
$\xi $
is a cyclic vector for
![]() $\pi $
, notice that
$\pi $
, notice that
![]() $\mathcal {H}_{\pi }=M+ \pi (t)M$
(where the sum is a priori not a direct sum). However, since
$\mathcal {H}_{\pi }=M+ \pi (t)M$
(where the sum is a priori not a direct sum). However, since
![]() $\mathcal {H}_{\pi }\not =M$
and since
$\mathcal {H}_{\pi }\not =M$
and since
![]() $t^2\in H$
, notice that
$t^2\in H$
, notice that
![]() $M\not \subseteq \pi (t)M$
. In particular, replacing N by
$M\not \subseteq \pi (t)M$
. In particular, replacing N by
![]() $N^\perp \cap M$
if necessary, we can assume that
$N^\perp \cap M$
if necessary, we can assume that
![]() $\mathcal {H}_{\pi }\not =N +\pi (t) M$
and therefore that
$\mathcal {H}_{\pi }\not =N +\pi (t) M$
and therefore that
![]() $\mathcal {H}_{\pi }\not = N+\pi (t)N $
. However,
$\mathcal {H}_{\pi }\not = N+\pi (t)N $
. However,
![]() $N+ \pi (t)N$
is a closed
$N+ \pi (t)N$
is a closed
![]() $\pi (G)$
-invariant subspace of
$\pi (G)$
-invariant subspace of
![]() $\pi $
. Since
$\pi $
. Since
![]() $\pi $
is irreducible, this implies that
$\pi $
is irreducible, this implies that
![]() $N+\pi (t)N=\{0\}$
and therefore that
$N+\pi (t)N=\{0\}$
and therefore that
![]() $N=\{0\}$
, which proves that
$N=\{0\}$
, which proves that
![]() $(\operatorname {\mathrm {Res}}_H^G(\pi ),M)$
is irreducible. Applying the same reasoning by taking
$(\operatorname {\mathrm {Res}}_H^G(\pi ),M)$
is irreducible. Applying the same reasoning by taking
![]() $\xi \in M^\perp $
, we also obtain that
$\xi \in M^\perp $
, we also obtain that
![]() $(\operatorname {\mathrm {Res}}_H^G(\pi ),M^\perp )$
is irreducible. In particular,
$(\operatorname {\mathrm {Res}}_H^G(\pi ),M^\perp )$
is irreducible. In particular,
![]() $\operatorname {\mathrm {Res}}_H^G$
decomposes as a direct sum of two irreducible representations of H. Let
$\operatorname {\mathrm {Res}}_H^G$
decomposes as a direct sum of two irreducible representations of H. Let
![]() $\sigma $
denote the irreducible representation
$\sigma $
denote the irreducible representation
![]() $(\operatorname {\mathrm {Res}}_H^G(\pi ),M)$
and notice from Theorem A.3 that
$(\operatorname {\mathrm {Res}}_H^G(\pi ),M)$
and notice from Theorem A.3 that
In particular,
![]() $\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma )$
, so that
$\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma )$
, so that
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )\leq \operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))$
. The result therefore follows from Lemma A.4, which ensures that
$\operatorname {\mathrm {Res}}_H^G(\pi )\leq \operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))$
. The result therefore follows from Lemma A.4, which ensures that
![]() $\operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))\cong \sigma \oplus \sigma ^t.$
$\operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))\cong \sigma \oplus \sigma ^t.$
Lemma A.6. Let
![]() $\pi $
be an irreducible representation of G such that
$\pi $
be an irreducible representation of G such that
![]() $\pi \cong \pi ^\tau $
. Then,
$\pi \cong \pi ^\tau $
. Then,
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
for some irreducible representation
$\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
for some irreducible representation
![]() $\sigma $
of H.
$\sigma $
of H.
Proof. Lemma A.5 ensures that
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )$
is either irreducible or split as desired. Suppose for a contradiction that
$\operatorname {\mathrm {Res}}_H^G(\pi )$
is either irreducible or split as desired. Suppose for a contradiction that
![]() $\sigma = \operatorname {\mathrm {Res}}_H^G(\pi )$
is irreducible and let
$\sigma = \operatorname {\mathrm {Res}}_H^G(\pi )$
is irreducible and let
![]() $\mathcal {U}: \mathcal {H}_{\pi }\rightarrow \mathcal {H}_{\pi }$
be the unitary operator intertwining
$\mathcal {U}: \mathcal {H}_{\pi }\rightarrow \mathcal {H}_{\pi }$
be the unitary operator intertwining
![]() $\pi $
and
$\pi $
and
![]() $\pi ^\tau $
. Notice that
$\pi ^\tau $
. Notice that
![]() $\pi $
and
$\pi $
and
![]() $\pi ^\tau $
have the same representation space
$\pi ^\tau $
have the same representation space
![]() ${\mathcal {H}_{\pi }}$
. Furthermore, for every
${\mathcal {H}_{\pi }}$
. Furthermore, for every
![]() $h\in H$
, we have that
$h\in H$
, we have that
![]() ${\pi (h)=\pi ^\tau (h)=\sigma (h)}$
. In particular,
${\pi (h)=\pi ^\tau (h)=\sigma (h)}$
. In particular,
![]() $\mathcal {U}$
is a unitary operator that intertwines
$\mathcal {U}$
is a unitary operator that intertwines
![]() $\sigma $
with itself. Since
$\sigma $
with itself. Since
![]() $\sigma $
is irreducible, this implies that
$\sigma $
is irreducible, this implies that
![]() $\mathcal {U}$
is a scalar multiple of the identity. However, this is impossible since for every
$\mathcal {U}$
is a scalar multiple of the identity. However, this is impossible since for every
![]() $h\in H$
and every
$h\in H$
and every
![]() $\xi \in \mathcal {H}_{\pi }$
,
$\xi \in \mathcal {H}_{\pi }$
,
We obtain as desired that
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
for some irreducible representation
$\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
for some irreducible representation
![]() $\sigma $
of H when
$\sigma $
of H when
![]() $\pi \cong \pi ^\tau $
.
$\pi \cong \pi ^\tau $
.
Proposition A.7. Let
![]() $\sigma $
be an irreducible representation of H. Then, the following hold:
$\sigma $
be an irreducible representation of H. Then, the following hold:
-
•
 $\sigma \not \cong \sigma ^t$
if and only if
$\sigma \not \cong \sigma ^t$
if and only if
 $\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is an irreducible representation of G and in that case
$\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is an irreducible representation of G and in that case
 $\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \operatorname {\mathrm {Ind}}_H^G(\sigma )^\tau $
;
$\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \operatorname {\mathrm {Ind}}_H^G(\sigma )^\tau $
; -
•
 $\sigma \cong \sigma ^t$
if and only if
$\sigma \cong \sigma ^t$
if and only if
 $\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi ^\tau $
for some irreducible representation
$\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi ^\tau $
for some irreducible representation
 $\pi $
of G.
$\pi $
of G.
Proof. Theorem A.3 ensures that
In particular, in light of Lemma A.4,
![]() $\mathrm {I}(\operatorname {\mathrm {Ind}}_H^G(\sigma ),\operatorname {\mathrm {Ind}}_H^G(\sigma ))=1$
(that is,
$\mathrm {I}(\operatorname {\mathrm {Ind}}_H^G(\sigma ),\operatorname {\mathrm {Ind}}_H^G(\sigma ))=1$
(that is,
![]() $\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is irreducible) if and only if
$\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is irreducible) if and only if
![]() $\sigma \not \cong \sigma ^t$
. Furthermore, in that case, Theorem A.3 ensures that
$\sigma \not \cong \sigma ^t$
. Furthermore, in that case, Theorem A.3 ensures that
 $$ \begin{align*} \mathrm{I}\big(\operatorname{\mathrm{Ind}}_H^G(\sigma),\operatorname{\mathrm{Ind}}_H^G(\sigma)^\tau\big)&=\mathrm{I}\big(\sigma,\operatorname{\mathrm{Res}}_H^G\big(\operatorname{\mathrm{Ind}}_H^G(\sigma)^\tau\big)\big)\\ &=\mathrm{I}\big(\sigma,\operatorname{\mathrm{Res}}_H^G\big(\operatorname{\mathrm{Ind}}_H^G(\sigma)\big)\big)\\ &=\mathrm{I}\big(\operatorname{\mathrm{Ind}}_H^G(\sigma),\operatorname{\mathrm{Ind}}_H^G(\sigma)\big)=1, \end{align*} $$
$$ \begin{align*} \mathrm{I}\big(\operatorname{\mathrm{Ind}}_H^G(\sigma),\operatorname{\mathrm{Ind}}_H^G(\sigma)^\tau\big)&=\mathrm{I}\big(\sigma,\operatorname{\mathrm{Res}}_H^G\big(\operatorname{\mathrm{Ind}}_H^G(\sigma)^\tau\big)\big)\\ &=\mathrm{I}\big(\sigma,\operatorname{\mathrm{Res}}_H^G\big(\operatorname{\mathrm{Ind}}_H^G(\sigma)\big)\big)\\ &=\mathrm{I}\big(\operatorname{\mathrm{Ind}}_H^G(\sigma),\operatorname{\mathrm{Ind}}_H^G(\sigma)\big)=1, \end{align*} $$
which proves that
![]() $\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \operatorname {\mathrm {Ind}}_H^G(\sigma )^\tau $
and settles the first case.
$\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \operatorname {\mathrm {Ind}}_H^G(\sigma )^\tau $
and settles the first case.
Now, suppose that
![]() $\sigma \cong \sigma ^t$
. In that case,
$\sigma \cong \sigma ^t$
. In that case,
![]() $\operatorname {\mathrm {Ind}}_H^G(\mathcal {H}_{\sigma })$
must split as a sum of two nonzero closed G-invariant subspaces M and
$\operatorname {\mathrm {Ind}}_H^G(\mathcal {H}_{\sigma })$
must split as a sum of two nonzero closed G-invariant subspaces M and
![]() $M'$
. However, since
$M'$
. However, since
![]() $\operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))$
splits as a sum of two irreducible representations of H by Lemma A.4, and since every G-invariant subspace is H-invariant, M and
$\operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))$
splits as a sum of two irreducible representations of H by Lemma A.4, and since every G-invariant subspace is H-invariant, M and
![]() $M'$
do not admit any proper invariant subspaces. This proves that
$M'$
do not admit any proper invariant subspaces. This proves that
![]() $\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi '$
for some irreducible representations
$\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi '$
for some irreducible representations
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
of G. Furthermore, since
$\pi '$
of G. Furthermore, since
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )=\operatorname {\mathrm {Res}}_H^G(\pi ^\tau )$
, Theorem A.3 ensures that
$\operatorname {\mathrm {Res}}_H^G(\pi )=\operatorname {\mathrm {Res}}_H^G(\pi ^\tau )$
, Theorem A.3 ensures that
for every irreducible representation
![]() $\pi $
of G. In particular, if
$\pi $
of G. In particular, if
![]() $\pi \not \cong \pi ^\tau $
, we obtain that
$\pi \not \cong \pi ^\tau $
, we obtain that
![]() $\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi ^\tau $
. However, if
$\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi ^\tau $
. However, if
![]() $\pi \cong \pi ^\tau $
, notice from Lemma A.6 that
$\pi \cong \pi ^\tau $
, notice from Lemma A.6 that
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
. Hence, since
$\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
. Hence, since
![]() $\sigma \cong \sigma ^t$
, Theorem A.3 implies that
$\sigma \cong \sigma ^t$
, Theorem A.3 implies that
which proves that
![]() $\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi \cong \pi \oplus \pi ^\tau $
.
$\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi \cong \pi \oplus \pi ^\tau $
.
The first part of Theorem A.2 follows from Lemmas A.4, A.5, A.6, Proposition A.7, and from the impossibility to have simultaneously that
![]() $\pi \cong \pi ^\tau $
and that
$\pi \cong \pi ^\tau $
and that
![]() $\sigma \cong \sigma ^t$
. Indeed, if
$\sigma \cong \sigma ^t$
. Indeed, if
![]() $\pi \cong \pi ^\tau $
, Lemma A.6 ensures that
$\pi \cong \pi ^\tau $
, Lemma A.6 ensures that
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
. However, if
$\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
. However, if
![]() $\sigma \cong \sigma ^t$
, Proposition A.7 ensures that
$\sigma \cong \sigma ^t$
, Proposition A.7 ensures that
![]() $\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi ^\tau $
. In particular, if these conditions were satisfied simultaneously, one would obtain that
$\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi ^\tau $
. In particular, if these conditions were satisfied simultaneously, one would obtain that
which is impossible since Proposition A.7 ensures that
The following result completes the proof of Theorem A.2.
Lemma A.8. Every irreducible representation
![]() $\pi $
of G satisfies
$\pi $
of G satisfies
![]() $\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma )$
for some irreducible representation
$\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma )$
for some irreducible representation
![]() $\sigma $
of H and every irreducible representation
$\sigma $
of H and every irreducible representation
![]() $\sigma $
of H satisfies
$\sigma $
of H satisfies
![]() $\sigma \leq \operatorname {\mathrm {Res}}_H^G(\pi )$
for some irreducible representation
$\sigma \leq \operatorname {\mathrm {Res}}_H^G(\pi )$
for some irreducible representation
![]() $\pi $
of G.
$\pi $
of G.
Proof. Let
![]() $\pi $
be an irreducible representation of G and let us show that
$\pi $
be an irreducible representation of G and let us show that
![]() $\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma )$
for some irreducible representation
$\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma )$
for some irreducible representation
![]() $\sigma $
of H. Notice from Theorem A.3 that
$\sigma $
of H. Notice from Theorem A.3 that
which proves that
![]() $\pi \leq \operatorname {\mathrm {Ind}}_H^G(\operatorname {\mathrm {Res}}_H^G(\pi ))$
. If
$\pi \leq \operatorname {\mathrm {Ind}}_H^G(\operatorname {\mathrm {Res}}_H^G(\pi ))$
. If
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )$
is irreducible, the result follows trivially. However, if
$\operatorname {\mathrm {Res}}_H^G(\pi )$
is irreducible, the result follows trivially. However, if
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )$
is not irreducible, Lemma A.5 ensures that
$\operatorname {\mathrm {Res}}_H^G(\pi )$
is not irreducible, Lemma A.5 ensures that
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
for some irreducible representation
$\operatorname {\mathrm {Res}}_H^G(\pi )\cong \sigma \oplus \sigma ^t$
for some irreducible representation
![]() $\sigma $
of H. In particular, since
$\sigma $
of H. In particular, since
![]() $\pi \leq \operatorname {\mathrm {Ind}}_H^G(\operatorname {\mathrm {Res}}_H^G(\pi )) \cong \operatorname {\mathrm {Ind}}_H^G(\sigma )\oplus \operatorname {\mathrm {Ind}}_H^G(\sigma ^t)$
, we obtain either that
$\pi \leq \operatorname {\mathrm {Ind}}_H^G(\operatorname {\mathrm {Res}}_H^G(\pi )) \cong \operatorname {\mathrm {Ind}}_H^G(\sigma )\oplus \operatorname {\mathrm {Ind}}_H^G(\sigma ^t)$
, we obtain either that
![]() $\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma )$
or that
$\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma )$
or that
![]() $\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma ^t)$
.
$\pi \leq \operatorname {\mathrm {Ind}}_H^G(\sigma ^t)$
.
Now, let
![]() $\sigma $
be an irreducible representation of H and let us show that
$\sigma $
be an irreducible representation of H and let us show that
![]() $\sigma \leq \operatorname {\mathrm {Res}}_H^G(\pi )$
for some irreducible representation
$\sigma \leq \operatorname {\mathrm {Res}}_H^G(\pi )$
for some irreducible representation
![]() $\pi $
of G. Notice from Theorem A.3 that
$\pi $
of G. Notice from Theorem A.3 that
which proves that
![]() $\sigma \leq \operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))$
. If
$\sigma \leq \operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))$
. If
![]() $\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is irreducible, the result follows trivially. However, if
$\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is irreducible, the result follows trivially. However, if
![]() $\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is not irreducible, Proposition A.7 ensures that
$\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is not irreducible, Proposition A.7 ensures that
![]() $\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi ^\tau $
for some irreducible representation
$\operatorname {\mathrm {Ind}}_H^G(\sigma )\cong \pi \oplus \pi ^\tau $
for some irreducible representation
![]() $\pi $
of G. In particular, it follows that
$\pi $
of G. In particular, it follows that
![]() $\sigma \leq \operatorname {\mathrm {Res}}_H^G(\pi )$
or that
$\sigma \leq \operatorname {\mathrm {Res}}_H^G(\pi )$
or that
![]() $\sigma \leq \operatorname {\mathrm {Res}}_H^G(\pi ^\tau )$
.
$\sigma \leq \operatorname {\mathrm {Res}}_H^G(\pi ^\tau )$
.
Finally, as a consequence of Theorem 5.3 and of the correspondence provided by Theorem A.2, the following lemma ensures that every Radu group on a
![]() $(d_0,d_1)$
-semi-regular tree with
$(d_0,d_1)$
-semi-regular tree with
![]() $d_0,d_1\geq 6$
is uniformly admissible.
$d_0,d_1\geq 6$
is uniformly admissible.
Lemma A.9. Let G be a totally disconnected locally compact group and let H be a closed subgroup of index
![]() $2$
. Then, G is uniformly admissible if and only if H is uniformly admissible.
$2$
. Then, G is uniformly admissible if and only if H is uniformly admissible.
Proof. Suppose that G is uniformly admissible and let K be a compact open subgroup of H. Since H has index
![]() $2$
in G, it is a clopen subgroup of G, which implies that K is a compact open subgroup of G. Since G is uniformly admissible, there exists a constant
$2$
in G, it is a clopen subgroup of G, which implies that K is a compact open subgroup of G. Since G is uniformly admissible, there exists a constant
![]() $k_K\in \mathbb N$
such that
$k_K\in \mathbb N$
such that
![]() $\dim (\mathcal {H}_{\pi }^K)\leq k_K$
for every irreducible representation
$\dim (\mathcal {H}_{\pi }^K)\leq k_K$
for every irreducible representation
![]() $\pi $
of G. Let
$\pi $
of G. Let
![]() $\sigma $
be an irreducible representation of H. Theorem A.2 ensures that
$\sigma $
be an irreducible representation of H. Theorem A.2 ensures that
![]() $\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is either irreducible or splits as a sum of two irreducible representations of G. However, notice from Theorem A.3 that
$\operatorname {\mathrm {Ind}}_H^G(\sigma )$
is either irreducible or splits as a sum of two irreducible representations of G. However, notice from Theorem A.3 that
which implies that
![]() $\sigma \leq \operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))$
. All together, this proves that
$\sigma \leq \operatorname {\mathrm {Res}}_H^G(\operatorname {\mathrm {Ind}}_H^G(\sigma ))$
. All together, this proves that
and H is uniformly admissible.
Suppose now that H is uniformly admissible and let K be a compact open subgroup of G. Since H has index
![]() $2$
in G, it is a clopen subgroup of G and
$2$
in G, it is a clopen subgroup of G and
![]() $K\cap H$
is a compact open subgroup of H. Since H is uniformly admissible, this implies the existence of a constant
$K\cap H$
is a compact open subgroup of H. Since H is uniformly admissible, this implies the existence of a constant
![]() $k_{K\cap H}$
such that
$k_{K\cap H}$
such that
![]() $\dim (\mathcal {H}_{\sigma })\leq k_{K \cap H}$
for every irreducible representation
$\dim (\mathcal {H}_{\sigma })\leq k_{K \cap H}$
for every irreducible representation
![]() $\sigma $
of H. Furthermore, Theorem A.2 ensures that
$\sigma $
of H. Furthermore, Theorem A.2 ensures that
![]() $\operatorname {\mathrm {Res}}_H^G(\pi )$
is either an irreducible representation of G or splits as a direct sum of
$\operatorname {\mathrm {Res}}_H^G(\pi )$
is either an irreducible representation of G or splits as a direct sum of
![]() $2$
irreducible representations of H. This implies that
$2$
irreducible representations of H. This implies that
Hence, G is uniformly admissible.
Acknowledgements
I warmly thank Pierre-Emmanuel Caprace for all the insightful discussions we shared and for all his comments on preliminary versions of this paper. I am also very grateful to the anonymous referee for their suggestions in this paper review and for all their valuable comments.