Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T08:56:16.444Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME INFINITE PERMUTATION GROUPS AND RELATED FINITE LINEAR GROUPS

Part of: Representation theory of groups Permutation groups

Published online by Cambridge University Press:  25 October 2016

PETER M. NEUMANN ,
CHERYL E. PRAEGER  and
SIMON M. SMITH
PETER M. NEUMANN*
Affiliation:
The Queen’s College, Oxford, OX1 4AW, UK email peter.neumann@queens.ox.ac.uk
CHERYL E. PRAEGER
Affiliation:
School of Mathematics and Statistics, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia email cheryl.praeger@uwa.edu.au
SIMON M. SMITH
Affiliation:
School of Mathematics and Physics, College of Science, University of Lincoln, Brayford Pool, Lincoln, LN6 7TS, UK email sismith@lincoln.ac.uk
*
✉ peter.neumann@queens.ox.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This article began as a study of the structure of infinite permutation groups 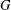$G$ in which point stabilisers are finite and all infinite normal subgroups are transitive. That led to two variations. One is the generalisation in which point stabilisers are merely assumed to satisfy min-n, the minimal condition on normal subgroups. The groups 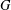$G$ are then of two kinds. Either they have a maximal finite normal subgroup, modulo which they have either one or two minimal nontrivial normal subgroups, or they have a regular normal subgroup 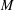$M$ which is a divisible abelian $p$ -group of finite rank. In the latter case the point stabilisers are finite and act irreducibly on a $p$ -adic vector space associated with 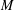 $M$ . This leads to our second variation, which is a study of the finite linear groups that can arise.

Keywords

infinite permutation groupsfinite groupsmodulesmodular representations

MSC classification

Primary: 20B07: General theory for infinite groups
Secondary: 20C05: Group rings of finite groups and their modules 20C10: Integral representations of finite groups 20C20: Modular representations and characters
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 102 , Issue 1 , February 2017 , pp. 136 - 149
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Bergman, George M. and Lenstra, Henrik W. Jr, ‘Subgroups close to normal subgroups’, J. Algebra 127 (1989), 80–97.Google Scholar
Curtis, Charles W. and Reiner, Irving, Representation Theory of Finite Groups and Associative Algebras (John Wiley, New York, 1962).Google Scholar
Droste, Manfred and Göbel, Rüdiger, ‘McLain groups over arbitrary rings and orderings’, Math. Proc. Cambridge Philos. Soc. 117 (1995), 439–467.Google Scholar
Fuchs, László, Infinite Abelian Groups, Vol. I (Academic Press, New York, 1970).Google Scholar
Hall, P., ‘Wreath powers and characteristically simple groups’, Proc. Cambridge Philos. Soc. 58 (1962), 170–184; also in Collected Works of Philip Hall (eds. K. W. Gruenberg and J. E. Roseblade) (Clarendon Press, Oxford, 1988), 611–625.CrossRefGoogle Scholar
James, Gordon, ‘On a conjecture of Carter concerning irreducible Specht modules’, Math. Proc. Cambridge Philos. Soc. 83 (1978), 11–17.Google Scholar
James, Gordon and Kerber, Adalbert, The Representation Theory of the Symmetric Group, Encyclopedia of Mathematics and its Applications, 16 (Addison-Wesley, Reading, MA, 1981).Google Scholar
McLain, D. H., ‘A characteristically simple group’, Proc. Cambridge Philos. Soc. 50 (1954), 641–642.CrossRefGoogle Scholar
Schlichting, G., ‘Operationen mit periodischen Stabilisatoren’, Arch. Math. (Basel) 34 (1980), 97–99.Google Scholar
Smith, Simon M., ‘A classification of primitive permutation groups with finite stabilisers’, J. Algebra 432 (2015), 12–21.CrossRefGoogle Scholar